Transmissionsförlust (kanalakustik)

Ljudmätningar
Karakteristisk	Symboler
Ljudtryck	p , SPL, L PA
Partikelhastighet	v , SVL
Partikelförskjutning	δ
Ljudintensitet	Jag , SIL
Ljudkraft	P , SWL, L WA
Ljud energi	W
Ljudenergitäthet	w
Ljudexponering	E , SEL
Akustisk impedans	Z
Ljudfrekvens	AF
Överföringsbortfall	TL

Transmissionsförlust (TL) i kanalakustik beskriver de akustiska prestanda hos ett ljuddämparliknande system. Det används ofta inom industriområdena som ljuddämpartillverkare och NVH (noise, vibration and harshness) avdelningen för biltillverkare och i akademiska studier. Generellt sett, ju högre överföringsförlust ett system har, desto bättre presterar det när det gäller brusreducering.

Introduktion

Transmissionsförlust (TL) i kanalakustik definieras som skillnaden mellan den effekt som infaller på en akustisk kanalanordning ( ljuddämpare ) och den som överförs nedströms till en ekofri avslutning. Överföringsförluster är oberoende av källan, om endast plana vågor inträffar vid enhetens inlopp. Transmissionsförluster involverar inte strålningsimpedansen eftersom den representerar skillnaden mellan infallande akustisk energi och den som överförs till en ekofri miljö. Genom att göras oberoende av termineringarna finner TL fördel hos forskare som ibland är intresserade av att hitta det akustiska överföringsbeteendet för ett element eller en uppsättning element isolerat från termineringarna. Men mätning av den infallande vågen i ett akustiskt fält för stående våg kräver användning av impedansrörsteknik, kan vara ganska mödosamt, om man inte använder sig av tvåmikrofonmetoden med modern instrumentering.

Matematisk definition

Transmissionsförlust (kanalakustik) definition illustration.

Per definition kan den plana vågen TL på en akustisk komponent med försumbart medelflöde beskrivas som:

$TL=L_{Wi}-L_{Wo}=10\log _{10}\left\vert {S_{i}p_{i+}v_{i+} \over 2}{2 \over S_{o }p_{o}v_{0}}\right\vert =10\log _{10}\left\vert {S_{i}p_{i+}^{2} \over S_{o}p_{o}^ {2}}\right\vert$

var:

• $L_{Wi}$ är den infallande ljudeffekten i inloppet som kommer mot ljuddämparen;
• $L_{Wo}$ är den överförda ljudeffekten som går nedströms i utloppet ur ljuddämparen;
• $S_{i},S_{o}$ står för tvärsnittsarean för ljuddämparens inlopp och utlopp
• $p_{i+}$ är det akustiska trycket från den infallande vågen i inloppet, mot ljuddämparen;
• $p_{o}$ är det akustiska trycket från den överförda vågen i utloppet, bort från ljuddämparen.
• $v_{i+}$ är partikelhastigheten för den infallande vågen i inloppet, mot ljuddämparen;
• $v_{o}$ är partikelhastigheten för den sända vågen i utloppet, bort från ljuddämparen.

Observera att $p_{i+}$ inte kan mätas direkt isolerat från det reflekterade vågtrycket $p_{i-}$ (i inloppet, bort från ljuddämparen). Man måste ta till impedansrörsteknik eller tvåmikrofonmetod med modern instrumentering. Men på nedströmssidan av ljuddämparen, $p_{o}=p_{o+}$ med tanke på den ekofria avslutningen, vilket säkerställer $p_{o-}= 0$ .

Och i de flesta ljuddämparapplikationer görs Si och So , arean på avgasröret och slutröret, i allmänhet lika, så vi har:

$TL=20\log _{10}\left\vert {p_{i+} \over p_{o}}\right\vert$

Således är TL lika med 20 gånger logaritmen (till basen 10) av förhållandet mellan det akustiska trycket associerat med den infallande vågen (i avgasröret) och det för den överförda vågen (i slutröret), där de två rören har samma tvärsnittsarea och slutröret avslutas ekofritt. Emellertid är detta ekofria tillstånd normalt svårt att möta under praktisk industrimiljö, så det är vanligtvis bekvämare för ljuddämpartillverkarna att mäta insticksförluster under deras ljuddämparprestandatest under arbetsförhållanden (monterad på en motor). Det finns emellertid inget samband mellan insättningsförlusten och överföringsförlusten hos en ljuddämpare.

Dessutom, eftersom den överförda ljudeffekten omöjligt kan överstiga den infallande ljudeffekten (eller $\left\vert p_{i+}\right\vert$$| {\displaystyle \left \vert p_{o}\right\vert }$ alltid större än ), är det känt att TL aldrig kommer att vara mindre än 0 dB.

Om systemet innehåller ett icke försumbart medelflöde och har kanalstorlekar som stöder våglägen av order som är högre än planvågsmoden vid de intressanta frekvenserna, ändras överföringsförlustberäkningarna i enlighet därmed.

Beskrivning av transmissionsmatrisen

Transmissionsförlust (kanalakustik) definitionsillustration med transmissionsmatris.

Lågfrekvensapproximationen innebär att varje delsystem är ett akustiskt tvåportar (eller fyrpoligt system) med två (och endast två) okända parametrar, de komplexa amplituder av två störande vågor som rör sig i motsatta riktningar. Ett sådant system kan beskrivas med sin transmissionsmatris (eller fyrpoliga matris), enligt följande

${\begin{bmatrix}{\hat {p}}_{i}\\{\hat {q }}_{i}\end{bmatrix}}={\begin{bmatrix}A&B\\C&D\end{bmatrix}}{\begin{bmatrix}{\hat {p}}_{o}\\{\ hatt {q}}_{o}\end{bmatrix}}$ ,

där ${\hat {p}}_{i}$ , ${\hat {p}}_{o}$ , ${\hat {q }}_{i}$ och ${\hat {q}}_{o}$ är ljudtrycken och volymhastigheterna vid ingången och vid utgången. A, B, C och D är komplexa tal. Med denna representation kan det bevisas att överföringsförlusten (TL) för detta delsystem kan beräknas som,

$TL=10\log _{10}\left({{1 \over 4}\ vänster\vert {A+B{S \över \rho c}+C{\rho c \over S}+D}\right\vert ^{2}}\right)$ ,

var:

• $S$ är inloppets och utloppets tvärsnittsarea;
• $\rho c$ är mediadensitet och ljudhastighet.

Ett enkelt exempel

Transmissionsförlust (kanalakustik) beräkning - ett enkelt exempel (enkammarljuddämpare).

Resultat av överföringsförlust (kanalakustik) beräkning - ett enkelt exempel (enkammarljuddämpare). c = 520 m/s vid 400°C; l = 0,5 m; h=1/3.

Med tanke på att vi har den enklaste reaktiva ljuddämparen med endast en expansionskammare (längd l och tvärsnittsarea S2), med inlopp och utlopp som båda har tvärsnittsarea S1). Som vi vet är transmissionsmatrisen för ett rör (i detta fall expansionskammaren).

${\begin{bmatrix}A&B\\C&D\end {bmatrix}}={\begin{bmatrix}{\cos kl}&{j{\rho c \over S_{2}}\sin kl}\\{j{S_{2} \over \rho c}\ sin kl}&{\cos kl}\end{bmatrix}}$ .

Ersätter ekvationen för TL ovan, kan det ses att TL för denna enkla reaktiva ljuddämpare är

${\begin {aligned}TL&=10\log _{10}\left({{1 \over 4}\left\vert {{\cos kl}+{j{S_{1} \over S_{2}}\sin kl }+{j{S_{2} \over S_{1}}\sin kl}+{\cos kl}}\right\vert ^{2}}\right)\\&=10\log _{10} \left({{\cos ^{2}kl}+{1 \over 4}\left(h+{1 \over h}\right)^{2}{\sin ^{2}kl}}\right) \\&=10\log _{10}\left({1+{1 \over 4}\left(h-{1 \over h}\right)^{2}{\sin ^{2}kl} }\right),\end{aligned}}$

där $h$ är förhållandet mellan tvärsnittsareorna och $l$ är längden på kammaren. $k=\omega /c$ är vågtalet medan $c$ är ljudhastigheten. Observera att överföringsförlusten är noll när $l$ är en multipel av en halv våglängd.

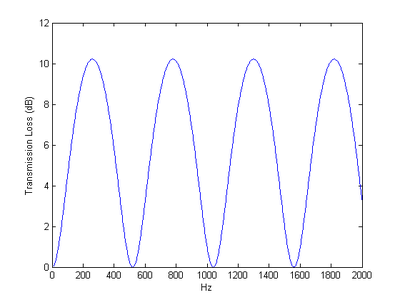
Som ett enkelt exempel, betrakta en enkammarljuddämpare med h = S1 / S2 =1/3, vid cirka 400 °C är ljudhastigheten cirka 520 m/s, med l =0,5 m, kan man enkelt beräkna TL-resultatet som visas på tomten till höger. Observera att TL är lika med noll när frekvensen är en multipel av $c \over {2l}$ och TL toppar när frekvensen är ${c \over {4l} }+{n*{c \over {2l}}}$ .

Observera också att ovanstående beräkning endast gäller för lågfrekvensområdet eftersom ljudvågen vid lågfrekvensområdet kan behandlas som en plan våg. TL-beräkningen kommer att börja förlora sin noggrannhet när frekvensen går över gränsfrekvensen , vilket kan beräknas som $f_{c}=1,84{c \over {\pi D}}$ , där D är diametern på det största röret i strukturen. I fallet ovan, om till exempel ljuddämparkroppen har en diameter på 300 mm, är gränsfrekvensen då 1,84*520/pi/0,3=1015 Hz.