Torus sammankoppling

En torus - interconnect är en switchfri nätverkstopologi för att ansluta bearbetningsnoder i ett parallellt datorsystem .

Diagram över en 3-dimensionell torus sammankoppling. Den är inte begränsad till 8 noder utan kan bestå av valfritt antal noder i en liknande rätlinjig array.

Introduktion

I geometri skapas en torus genom att rotera en cirkel runt en axel i samma plan som cirkeln. Även om detta är en allmän definition inom geometri, beskriver de topologiska egenskaperna för denna typ av form nätverkstopologin i dess väsen.

Geometri illustration

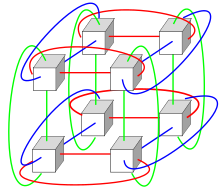
Följande bilder är 1D och 2D torus. 1D torus är en enkel cirkel, och 2D torus har formen av en munk. Animationen nedan illustrerar hur en 2D-torus genereras från en rektangel genom att koppla samman dess två par av motsatta kanter. Här används begreppet torus för att i huvudsak beskriva början och slutet av en sekvens av noder som är anslutna, som en munk. För att bättre illustrera konceptet och förstå vad topologin betyder i nätverkssammankoppling ger vi 3 exempel på parallella sammankopplade noder som använder torustopologi. Vid en dimension är en torustopologi likvärdig med ett ringförbindelsenätverk , i form av en cirkel. Vid 2D motsvarar det ett 2D-nät, men med extra anslutning vid kantnoderna, vilket är definitionen av 2D-torus.

1D torus exempel, en cirkel.
2D torus exempel, en munk.
Generera en 2D-torus från en 2D-rektangel.

Torus nätverkstopologi

Vi kan generalisera regeln från figurerna ovan. Torus-interconnect är en switch-fri topologi som kan ses som en mesh-interconnect med noder arrangerade i en rätlinjig uppsättning av N = 2, 3 eller fler dimensioner, med processorer anslutna till sina närmaste grannar och motsvarande processorer på motsatta kanter av array ansluten. [1] I detta gitter har varje nod 2N anslutningar. Denna topologi fick namnet från det faktum att gittret som bildas på detta sätt är topologiskt homogent till en N-dimensionell torus .

Visualisering

De tre första dimensionerna av torus-nätverkstopologi är lättare att visualisera och beskrivs nedan:

1D Torus illustration
2D Torus illustration
3D Torus illustration

1D Torus: det är en dimension, n noder är anslutna i sluten slinga med varje nod ansluten till sina 2 närmaste grannar kommunikation kan ske i 2 riktningar, +x och −x. 1D Torus är samma som ringsammankoppling .
2D Torus: det är tvådimensionellt med graden 4, noderna föreställs utlagda i ett tvådimensionellt rektangulärt gitter med n rader och n kolumner, med varje nod ansluten till sina 4 närmaste grannar och motsvarande noder på motsatta kanter anslutna. Anslutningen av motsatta kanter kan visualiseras genom att rulla den rektangulära uppsättningen till ett "rör" för att ansluta två motsatta kanter och sedan böja "röret" till en torus för att ansluta de andra två. kommunikation kan ske i fyra riktningar, +x, −x, +y och −y. Den totala noderna för 2D Torus är n ² .
3D Torus: det är tredimensionellt, noderna föreställs i ett tredimensionellt gitter i form av ett rektangulärt prisma, med varje nod ansluten till sina 6 grannar, med motsvarande noder på motsatta ytor av arrayen anslutna. Varje kant består av n noder. kommunikation kan ske i 6 riktningar, +x, −x, +y, −y, +z, −z. Varje kant av 3D Torus består av n noder. Det totala antalet noder för 3D Torus är n ³ .
ND Torus: den kan ha N dimension, varje nod av N dimension Torus har 2N grannar, kommunikation kan ske i 2N riktningar. Varje kant består av n noder. Totala noder för denna torus är n ^N . Den främsta motivationen för att ha en högre dimension av torus är att uppnå högre bandbredd, lägre latens och högre skalbarhet.

Högdimensionella arrayer är svåra att visualisera men vi kan se ovanstående regel att varje högre dimension lägger till ytterligare ett par närmaste grannanslutningar till varje nod.

Prestanda

Ett antal superdatorer på TOP500- listan använder tredimensionella torusnätverk, t.ex. IBM:s Blue Gene/L och Blue Gene/P , och Cray XT3. IBM:s Blue Gene/Q använder ett femdimensionellt torusnätverk. Fujitsus K-dator och PRIMEHPC FX10 använder en egenutvecklad tredimensionell torus 3D-mesh-interconnect som kallas Tofu.

3D Torus prestandasimulering

Sandeep Palur och Dr. Ioan Raicu från Illinois Institute of Technology genomförde experiment för att simulera 3D-torusprestanda. Deras experiment kördes på en dator med 250 GB RAM, 48 kärnor och x86_64-arkitektur. Simulatorn de använde var ROSS (Rensselaers Optimistic Simulation System). De fokuserade huvudsakligen på tre aspekter:

Varierande nätverksstorlek
Varierande antal servrar
Varierande meddelandestorlek

De drog slutsatsen att genomströmningen minskar med ökningen av servrar och nätverksstorlek. Annars ökar genomströmningen med ökningen av meddelandestorleken.

6D Torus produktprestanda

Fujitsu Limited utvecklade en 6D torus datormodell kallad "Tofu". I deras modell kan en 6D-torus uppnå 100 GB/s off-chip-bandbredd, 12 gånger högre skalbarhet än en 3D-torus och hög feltolerans. Modellen används i K-datorn och Fugaku .

Fördelar och nackdelar

Fördelar

Högre hastighet, lägre latens: På grund av anslutningen av motsatta kanter har data fler alternativ att resa från en nod till en annan, vilket kraftigt ökade hastigheten.
Bättre rättvisa: I en 4×4 mesh-interconnect är det längsta avståndet mellan noderna från övre vänstra hörnet till nedre högra hörnet. Varje datum tar 6 hopp för att resa den längsta vägen. Men i en 4×4 Torus-förbindelse kan det övre vänstra hörnet gå till det nedre högra hörnet med endast 2 hopp.
Lägre energiförbrukning: Eftersom data tenderar att gå färre hopp, tenderar energiförbrukningen att vara lägre.

Nackdelar

Kabeldragningens komplexitet: Extra kablar kan försvåra dragningsprocessen i den fysiska designfasen. Om vi vill lägga ut fler ledningar på chip, är det troligt att vi behöver öka antalet metallskikt eller minska tätheten på chip, vilket är dyrare. Annars kan ledningarna som ansluter motsatta kanter vara mycket längre än andra kablar. Denna ojämlikhet mellan länklängder kan orsaka problem på grund av RC-fördröjning .
Kostnad: Även om långa omslutande länkar kan vara det enklaste sättet att visualisera anslutningstopologin, gör begränsningar av kabellängder ofta långa omslagslänkar opraktiska i praktiken. Istället är direkt anslutna noder – inklusive noder som ovanstående visualisering placerar på motsatta kanter av ett rutnät, sammankopplade med en lång omslutande länk – fysiskt placerade nästan intill varandra i ett vikt torusnätverk. Varje länk i det vikta torusnätverket är mycket kort - nästan lika kort som de närmaste grannlänkarna i en enkel nätsammankoppling - och därför låg latens.

Se även