Tilläggsprincip

A collection of five dots and one of zero dots merge into one of five dots.

5+0=5 illustrerad med samlingar av prickar.

Inom kombinatorik är additionsprincipen eller summaregeln en grundläggande räkneprincip . Enkelt uttryckt är det den intuitiva idén att om vi har ett antal sätt att göra något och B antal sätt att göra en annan sak och vi inte kan göra båda samtidigt, så finns det $A+ B$ sätt att välja en av åtgärderna. I matematiska termer anger additionsprincipen att vi för disjunkta mängder A och B har $|A\cup B|=|A|+|B|$ .

Summeregeln är ett faktum om mängdlära . ^{[ citat behövs ]}

Tilläggsprincipen kan utökas till flera uppsättningar. Om $S_{1},S_{2},\ldots ,S_{n}$ är parvis disjunkta uppsättningar, så har vi:

|S_{1}|+|S_{2}|+\cdots +|S_{n}|=|S_{1}\cup S_{2}\cup \cdots \cup S_{n}|.

Detta påstående kan bevisas från additionsprincipen genom induktion på n .

Enkelt exempel

Five shapes split into a group of three shapes and one of two shapes.

3+2=5 illustrerade med former.

En person har bestämt sig för att handla i en butik idag, antingen i norra delen av stan eller södra delen av stan. Om de besöker den norra delen av staden kommer de att handla i antingen ett köpcentrum, en möbelaffär eller en smyckesbutik (3 sätt). Om de besöker den södra delen av staden kommer de att handla i antingen en klädaffär eller en skoaffär (2 sätt).

Det finns alltså $3+2=5$ möjliga butiker som personen skulle kunna handla i idag.

Principen för inkludering–uteslutning

A series of Venn diagrams illustrating the principle of inclusion-exclusion.

En serie Venn-diagram som illustrerar principen för inkludering-uteslutning.

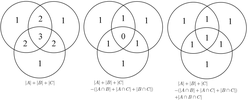
Inklusions -exkluderingsprincipen (även känd som sållprincipen ) kan ses som en generalisering av summaregeln genom att den också räknar upp antalet element i föreningen av vissa mängder (men kräver inte att mängderna är disjunkta ). Den anger att om A ₁ , ..., A _n är ändliga mängder, då

\left|\bigcup _{i=1}^{n}A_{i}\right|=\summa _{i=1}^{n}\left|A_{i}\right|-\ summa _{i,j\,:\,1\leq i<j\leq n}\left|A_{i}\cap A_{j}\right|+\summa _{i,j,k\,: \,1\leq i<j<k\leq n}\left|A_{i}\cap A_{j}\cap A_{k}\right|-\ \cdots \ +(-1)^{n- 1}\left|A_{1}\cap \cdots \cap A_{n}\right|.

Subtraktionsprincip

På liknande sätt, för en given finit mängd S, och givet en annan mängd A, om $A\subset S$ , då $|A^{c}|=|S|-|A|$ . För att bevisa detta, lägg märke till att $|A^{c}|+|A|=|S|$ genom additionsprincipen.

Ansökningar

Additionsprincipen kan användas för att bevisa Pascals regel kombinatoriskt. För att beräkna ${\binom {n+1}{k}}$ kan man se det som antalet sätt att välja k personer från ett rum som innehåller n barn och 1 lärare. Sedan finns det ${\binom {n}{k}}$ sätt att välja personer utan att välja lärare, och ${\binom {n}{k-1 }}$ sätt att välja personer som inkluderar läraren. Således ${\binom {n+1}{k}}={\binom {n}{k}}+{\binom { n}{k-1}}$ .

Additionsprincipen kan också användas för att bevisa multiplikationsprincipen .

Bibliografi

Biggs, Norman L. (2002). Diskret matematik . Indien: Oxford University Press . ISBN 978-0-19-871369-2 .

Se även