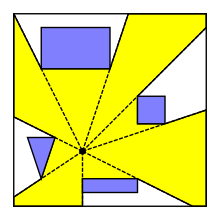
Synlighetspolygon

Synlighetspolygon visas i gult. Fyra hinder visas i blått.

I beräkningsgeometri är siktpolygonen eller siktområdet för en punkt $p$ i planet bland hindren den möjligen obegränsade polygonregionen för alla punkter i planet som är synliga från $p$ . Synlighetspolygonen kan också definieras för synlighet från ett segment eller en polygon. Synlighetspolygoner är användbara i robotik , videospel och i olika optimeringsproblem som t.ex. lokaliseringsproblemet och konstgalleriproblemet .

Om synlighetspolygonen är avgränsad är det en stjärnformad polygon . En siktpolygon begränsas om alla strålar som skjuter från punkten slutligen slutar i något hinder. Detta är fallet, t.ex. om hindren är kanterna på en enkel polygon och $p$ är inuti polygonen. I det senare fallet kan synlighetspolygonen hittas i linjär tid .

Definitioner

Formellt kan vi definiera det plana synbarhetspolygonproblemet som sådant. Låt $S$ vara en uppsättning av hinder (antingen segment eller polygoner) i $\mathbb {R} ^{2}$ . Låt $p$ vara en punkt i $\mathbb {R} ^{2}$ som inte är inom ett hinder. Sedan punktsynlighetspolygonen $V$ uppsättningen av punkter i ${\displaystyle \mathbb {R} ^{2}},$ så att för varje punkt $q$ i $V$ , segmentet $pq$ skär inte något hinder i $S$ .

På samma sätt är segmentsynlighetspolygonen eller kantsynlighetspolygonen den del som är synlig för någon punkt längs ett linjesegment .

Ansökningar

Synlighetspolygoner är användbara i robotteknik . Till exempel, vid robotlokalisering kommer en robot som använder sensorer som en lidar att upptäcka hinder som den kan se, vilket liknar en synlighetspolygon.

De är också användbara i videospel , med många onlinehandledningar som förklarar enkla algoritmer för att implementera det.

Algoritmer för punktsynlighetspolygoner

Många algoritmer har föreslagits för att beräkna punktsynlighetspolygonen. För olika varianter av problemet (t.ex. olika typer av hinder) varierar algoritmerna i tidskomplexitet.

Naiva algoritmer

Naiva algoritmer är lätta att förstå och implementera, men de är inte optimala eftersom de kan vara mycket långsammare än andra algoritmer.

Uniform "fysisk" algoritm för strålgjutning

I det verkliga livet lyser en glödpunkt upp området som är synligt för det eftersom det avger ljus i alla riktningar. Detta kan simuleras genom att skjuta strålar i många riktningar. Antag att punkten är $p$ och mängden hinder är $S$ . Sedan pseudokoden uttryckas på följande sätt:

    
     
        
        
      algorithm  naive_bad_algorithm(  $p$  ,  $S$  )  är  $V$  :=  $\emptyset$  för  $\theta =0,\ cdots ,2\pi$  : // skjuta en stråle med vinkeln  $\theta$  $r$  :=  $\infty$  för varje  hinder i  $S$  :  ${\ displaystyle r}$  := min(  $r$  , avstånd från  $p$  till hindret i denna riktning) lägg till vertex  $(\theta ,r)$  till  ${\ displaystyle V}$  returnera  $V$

Om det nu vore möjligt att prova alla de oändligt många vinklarna skulle resultatet bli korrekt. Tyvärr är det omöjligt att verkligen prova varenda riktning på grund av datorernas begränsningar. En approximation kan skapas genom att kasta många, säg, 50 strålar fördelade på jämnt mellanrum. Detta är dock inte en exakt lösning, eftersom små hinder helt och hållet kan missas av två intilliggande strålar. Dessutom är det väldigt långsamt, eftersom man kan behöva skjuta många strålar för att få en ungefär liknande lösning, och polygonen för utgående synlighet kan ha många fler hörn i sig än nödvändigt.

Strålkastning till varje vertex

Den tidigare beskrivna algoritmen kan förbättras avsevärt i både hastighet och korrekthet genom att observera att det räcker med att bara skjuta strålar till varje hinders hörn. Detta beror på att eventuella böjar eller hörn längs gränsen för en siktpolygon måste bero på något hörn (dvs. en vertex) i ett hinder.

    
    
            
            
            
      algorithm  naive_better_algorithm(  $p$  ,  $S$  )  är  $V$  :=  $\emptyset$  för varje  hinder  $b$  i  $S$  :  för varje  vertex  $v$  av  $b$  : // skjut en stråle från  $p$  till  $v$  $r$  := avstånd från  $p$  till  $v$  $\theta$  := vinkel på  $v$  med avseende på  $p$  för varje  hinder  $b'$  i  ${\ displaystyle S}$  :  $r$  := min(  $r$  , avstånd från  $p$  till  $b'$  ) lägg till vertex  $( \theta ,r)$  till  $V$  returnera  $V$

Algoritmen ovan kanske inte är korrekt. Se diskussionen under Diskussion.

Tidskomplexiteten för denna algoritm är $O(n^{2})$ . Detta beror på att algoritmen skjuter en stråle till vart och ett av de $n$ hörnen, och för att kontrollera var strålen slutar måste den leta efter korsning med var och en av $O(n) )$ hinder. Detta är tillräckligt för många enkla applikationer som videospel, och som sådan lär många onlinetutorials ut denna metod. Men som vi ska se senare finns det snabbare $O(n\log n)$ algoritmer (eller ännu snabbare om hindret är en enkel polygon eller om det finns ett fast antal polygonala hål).

Optimala algoritmer för en punkt i en enkel polygon

En synlig polygon för en punkt i mitten (visad i vitt) inuti en enkel polygon, med svart kontur.

Givet en enkel polygon ${\mathcal {P}}$ och en punkt $p$ , är en linjär tidsalgoritm optimal för att beräkna regionen i ${\mathcal {P}}$ som är synlig från $p$ . En sådan algoritm föreslogs första gången 1981. Den är dock ganska komplicerad. 1983 föreslogs en konceptuellt enklare algoritm, som hade ett mindre fel som korrigerades 1987.

Den senare algoritmen kommer att förklaras kort här. Den går helt enkelt runt gränsen för polygonen ${\mathcal {P}}$ och bearbetar hörnen i den ordning som de visas, samtidigt som den bibehåller en stapel med hörn ${\mathcal {S}}=s_{0},s_{1},\cdots ,s_{t}$ där $s_{t}$ är toppen av stacken. Stacken utgör de hörn som har påträffats hittills och som är synliga för $p$ . Om, senare under exekveringen av algoritmen, några nya hörn påträffas som skymmer en del av ${\displaystyle {\mathcal {S}}} , då$ kommer de dolda hörnen i ${\displaystyle {\mathcal {S}}} att$ plockas ur högen. När algoritmen avslutas ${\mathcal {S}}$ att bestå av alla synliga hörn, dvs den önskade synlighetspolygonen. En effektiv implementering publicerades 2014.

Optimala algoritmer för en punkt i en polygon med hål

För en punkt i en polygon med $h$ hål och totalt ${\displaystyle n} hörn, kan det visas att i värsta fall, en$ ${\displaystyle \Theta (n+h\log h)}-$ algoritmen är optimal. En sådan algoritm föreslogs 1995 tillsammans med dess bevis på optimalitet. Den förlitar sig dock på den linjära tidspolygontrianguleringsalgoritmen av Chazelle, som är extremt komplex.

Optimala algoritmer för en punkt bland segmenten

Segment som inte skär varandra förutom vid deras slutpunkter

En synlighetspolygon för en punkt i mitten (visad i vitt) bland en uppsättning godtyckliga linjesegment i planet, tillåten att skära endast vid deras ändpunkter och fungerar som hinder (visas i svart).

För en punkt bland en uppsättning av $n$ segment som inte skär varandra förutom vid deras ändpunkter, kan det visas att i värsta fall, en $\Theta (n\log n)$ algoritmen är optimal. Detta beror på att en synlighetspolygonalgoritm måste mata ut hörn på synlighetspolygonen i sorterad ordning, varför problemet med sortering kan reduceras till att beräkna en synlighetspolygon.

Lägg märke till att vilken algoritm som helst som beräknar en synlighetspolygon för en punkt bland segment kan användas för att beräkna en synlighetspolygon för alla andra typer av polygonala hinder, eftersom vilken polygon som helst kan delas upp i segment.

Söndra och erövra

En dela-och-härska-algoritm för att beräkna synlighetspolygonen föreslogs 1987.

Vinkelsvep

En vinkelsvep , dvs rotationsplanssvepalgoritm för att beräkna synlighetspolygonen föreslogs 1985 och 1986. Tanken är att först sortera alla segmentändpunkter efter polär vinkel och sedan iterera över dem i den ordningen. Under iterationen bibehålls händelseraden som en hög . En effektiv implementering publicerades 2014.

I allmänhet korsande segment

För en punkt bland generellt korsande segment är synbarhetspolygonproblemet reducerbart, i linjär tid, till det undre enveloppproblemet . Enligt Davenport–Schinzel-argumentet har det nedre kuvertet i värsta fall $\Theta (n\alpha (n))$ antal hörn, där $\ alfa (n)$ är den omvända Ackermann-funktionen . En optimal dela-och-härska-algoritm i värsta fall som körs i ${\displaystyle \Theta (n\log n)}-$ tid skapades av John Hershberger 1989.

^ Franco P. Preparata och Michael Ian Shamos (1985). Computational Geometry - En introduktion . Springer-Verlag . 1:a upplagan: ISBN 0-387-96131-3 ; 2:a tryckningen, korrigerad och utökad, 1988: ISBN 3-540-96131-3 ; Rysk översättning, 1989: ISBN 5-03-001041-6 .
^ ^a ^b El Gindy, Hossam; Avis, David (1981). "En linjär algoritm för att beräkna synlighetspolygonen från en punkt". Journal of Algorithms . 2 (2): 186–197. doi : 10.1016/0196-6774(81)90019-5 .
^ ^a ^b Lee, DT (maj 1983). "Synlighet av en enkel polygon". Datorseende, grafik och bildbehandling . 22 (2): 207–221. doi : 10.1016/0734-189X(83)90065-8 .
^ ^a ^b Joe, Barry; Simpson, RB (1987). "Rättelser till Lees synlighetspolygonalgoritm". BIT Numerisk matematik . 27 (4): 458–473. doi : 10.1007/BF01937271 .
^ Guibas, Leonidas; Motwani, Rajeev; Raghavan, Prabhakar (1992). Robotlokaliseringsproblemet i två dimensioner . ACM-SIAM symposium om diskreta algoritmer. Föreningen för industriell och tillämpad matematik.
^ Liow, Nicklaus. "SYN & LJUS hur man skapar 2D-synlighet/skuggeffekter för ditt spel" . Hämtad 9 maj 2014 .
^ Patel, Amit (5 juli 2012). "2d Synlighetsalgoritm" . Hämtad 9 maj 2014 .
^ ^a ^b Patel, Amit (5 juli 2012). "Blobs in Games: 2d Visibility" . Hämtad 9 maj 2014 .
^ ^a ^b Bungiu, Francisc; Hemmer, Michael; Hershberger, John; Huang, Kan; Kröller, Alexander (2014). "Effektiv beräkning av synlighetspolygoner". arXiv : 1403.3905 [ cs.CG ].
^ Heffernan, Paul; Mitchell, Joseph (1995). "En optimal algoritm för att beräkna synlighet i planet" (PDF) . SIAM Journal on Computing . 24 (1): 184–201. doi : 10.1137/S0097539791221505 . hdl : 1813/8838 .
^ ^a ^b Suri, Subhash; O'Rourke, Joseph (1986). Värsta tänkbara optimala algoritmer för att konstruera synlighetspolygoner med hål . Symposium om beräkningsgeometri. ACM . s. 14–23. doi : 10.1145/10515.10517 .
^ Arkin, E. ; Mitchell, Joseph (1987). En optimal synlighetsalgoritm för en enkel polygon med stjärnformade hål ( Teknisk rapport). Cornell University Operations Research and Industrial Engineering. 746.
^ Asano, Tetsuo (1985). En effektiv algoritm för att hitta synlighetspolygonen för en polygonregion med hål . Institutet för elektronik-, informations- och kommunikationsingenjörer. Vol. 68. s. 557–559.
^ Hershberger, John (1989). "Hitta den övre envelopen av $n$ linjesegment i $O(n\log n)$ tid". Informationsbehandlingsbrev . 33 (4): 169–174. doi : 10.1016/0020-0190(89)90136-1 .

externa länkar

http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en (synlighet i enkla polygoner - applets)

programvara

VisiLibity : Ett gratis C++-bibliotek med öppen källkod för synlighetsberäkningar i plana polygonala miljöer.
visibility-polygon-js : Ett JavaScript-bibliotek för allmän egendom för att beräkna en synlighetspolygon för en punkt bland segmenten med hjälp av metoden vinkelsvep.

[PS-1] Franco P. Preparata och Michael Ian Shamos (1985). Computational Geometry - En introduktion . Springer-Verlag . 1:a upplagan: ISBN 0-387-96131-3 ; 2:a tryckningen, korrigerad och utökad, 1988: ISBN 3-540-96131-3 ; Rysk översättning, 1989: ISBN 5-03-001041-6 .

[ea-2] El Gindy, Hossam; Avis, David (1981). "En linjär algoritm för att beräkna synlighetspolygonen från en punkt". Journal of Algorithms . 2 (2): 186–197. doi : 10.1016/0196-6774(81)90019-5 .

[lee-3] Lee, DT (maj 1983). "Synlighet av en enkel polygon". Datorseende, grafik och bildbehandling . 22 (2): 207–221. doi : 10.1016/0734-189X(83)90065-8 .

[js-4] Joe, Barry; Simpson, RB (1987). "Rättelser till Lees synlighetspolygonalgoritm". BIT Numerisk matematik . 27 (4): 458–473. doi : 10.1007/BF01937271 .

[guibas-5] Guibas, Leonidas; Motwani, Rajeev; Raghavan, Prabhakar (1992). Robotlokaliseringsproblemet i två dimensioner . ACM-SIAM symposium om diskreta algoritmer. Föreningen för industriell och tillämpad matematik.

[ncase-6] Liow, Nicklaus. "SYN & LJUS hur man skapar 2D-synlighet/skuggeffekter för ditt spel" . Hämtad 9 maj 2014 .

[redblob-7] Patel, Amit (5 juli 2012). "2d Synlighetsalgoritm" . Hämtad 9 maj 2014 .

[redblob2-8] Patel, Amit (5 juli 2012). "Blobs in Games: 2d Visibility" . Hämtad 9 maj 2014 .

[bungiu-9] Bungiu, Francisc; Hemmer, Michael; Hershberger, John; Huang, Kan; Kröller, Alexander (2014). "Effektiv beräkning av synlighetspolygoner". arXiv : 1403.3905 [ cs.CG ].

[hlogh-10] Heffernan, Paul; Mitchell, Joseph (1995). "En optimal algoritm för att beräkna synlighet i planet" (PDF) . SIAM Journal on Computing . 24 (1): 184–201. doi : 10.1137/S0097539791221505 . hdl : 1813/8838 .

[so-11] Suri, Subhash; O'Rourke, Joseph (1986). Värsta tänkbara optimala algoritmer för att konstruera synlighetspolygoner med hål . Symposium om beräkningsgeometri. ACM . s. 14–23. doi : 10.1145/10515.10517 .

[am-12] Arkin, E. ; Mitchell, Joseph (1987). En optimal synlighetsalgoritm för en enkel polygon med stjärnformade hål ( Teknisk rapport). Cornell University Operations Research and Industrial Engineering. 746.

[asano-13] Asano, Tetsuo (1985). En effektiv algoritm för att hitta synlighetspolygonen för en polygonregion med hål . Institutet för elektronik-, informations- och kommunikationsingenjörer. Vol. 68. s. 557–559.

[hershberger-14] Hershberger, John (1989). "Hitta den övre envelopen av $n$ linjesegment i $O(n\log n)$ tid". Informationsbehandlingsbrev . 33 (4): 169–174. doi : 10.1016/0020-0190(89)90136-1 .