Svagt kedjad diagonalt dominant matris

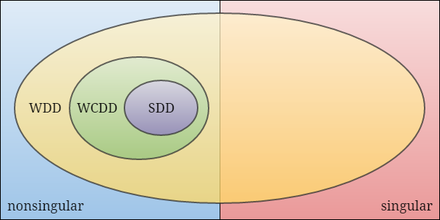
Venn Diagram som visar inneslutningen av svagt kedjade diagonalt dominanta (WCDD) matriser i förhållande till svagt diagonalt dominanta (WDD) och strikt diagonalt dominanta (SDD) matriser.

Inom matematik är de svagt kedjade diagonalt dominanta matriserna en familj av icke-singulära matriser som inkluderar de strikt diagonalt dominanta matriserna .

Definition

Förberedelser

Vi säger att rad $i$ i en komplex matris $A=(a_{ij})$ är strikt diagonalt dominant (SDD) om $|a_{ii}|>\textstyle {\sum _{j\neq i}}|a_{ij}|$ . Vi säger att $A$ är SDD om alla dess rader är SDD. Svagt diagonalt dominant (WDD) definieras med $\geq$ istället.

Den riktade grafen associerad med en $m\times m$ komplex matris $A=(a_{ij})$ ges av hörnen $\{1,\ldots ,m\}$ och kanter definierade enligt följande: det finns en kant från $i\rightarrow j$ om och endast om $a_{ij }\neq 0$ .

Definition

En komplex kvadratisk matris $A$ sägs vara svagt kedjad diagonalt dominant (WCDD) om

• $A$ är WDD och
• för varje rad ${\displaystyle i_{1}} som$ inte är SDD, finns det en promenad $i_{1}\rightarrow i_{2}\rightarrow \cdots \ högerpil i_{k}$ i den riktade grafen för $A$ som slutar på en SDD-rad $i_{k}$ .

Exempel

Den riktade grafen som är associerad med WCDD-matrisen i exemplet. Den första raden, som är SDD, är markerad. Observera att oavsett vilken nod $i$ vi börjar på, kan vi hitta en promenad $i\rightarrow (i-1)\ högerpil (i-2)\högerpil \cdots \rightarrow 1$ .

Matrisen $\displaystyle m\times m}$ {

${\begin{pmatrix}1\\-1&1\\&-1&1\\&&\ddots &\ddots \\&&&-1&1\end{pmatrix }}$

är WCDD.

Egenskaper

Icke singularitet

En WCDD-matris är icke-singular.

Bevis : Låt $A=(a_{ij})$ vara en WCDD-matris. Anta att det finns en icke-noll $x$ i nollutrymmet för $A$ . Utan förlust av generalitet, låt $i_{1}$ vara sådan att $|x_{i_{1}}|=1\geq |x_{j}|$ för alla $j$ . Eftersom $A$ är WCDD, kan vi välja en promenad ${\displaystyle i_{1}\rightarrow i_{2}\rightarrow \cdots \rightarrow i_{k}}-$ slut vid en SDD-rad $i_{k}$ .

Tar moduli på båda sidor av

$-a_{i_{1}i_{1}}x_{i_{1}}=\summa _{j\ neq i_{1}}a_{i_{1}j}x_{j}$

och att tillämpa triangelojämlikheten ger

$\left|a_{i_{1}i_{1}}\right|\leq \sum _{j\neq i_{1}}\left|a_{i_{1}j}\right|\ vänster|x_{j}\right|\leq \sum _{j\neq i_{1}}\left|a_{i_{1}j}\right|,$

och följaktligen är rad $i_{1}$ inte SDD. Dessutom, eftersom $A$ är WDD, gäller ovanstående kedja av ojämlikheter med likhet så att $|x_{j}|=1$ när $a_{i_{1}j}\neq 0$ . Därför $|x_{i_{2}}|=1$ . Genom att upprepa detta argument med $i_{2}$ , $i_{3}$ etc. finner vi att $i_{k}$ inte är SDD, en motsägelse. $\square$

Påminner om att en irreducerbar matris är en vars associerade riktade graf är starkt ansluten , en trivial följd av ovanstående är att en irreducerbart diagonalt dominant matris (dvs en irreducerbar WDD-matris med minst en SDD-rad) är icke-singular.

Förhållande med icke-singular M-matriser

Följande är likvärdiga:

• $A$ är en icke-singular WDD M-matris .
• $A$ är en icke-singular WDD L-matris ;
• $A$ är en WCDD L-matris ;

Faktum är att WCDD L-matriser studerades (av James H. Bramble och BE Hubbard) så tidigt som 1964 i en tidskriftsartikel där de förekommer under det alternativa namnet på matriser av positiv typ .

Dessutom, om $A$ är en $n\times n$ WCDD L-matris, kan vi binda dess invers enligt följande:

$\left\Vert A^{-1}\right\Vert _{\infty }\ leq \sum _{i}\left[a_{ii}\prod _{j=1}^{i}(1-u_{j})\right]^{-1}$ där $u_{i}={\frac {1}{\left|a_{ii}\right|}}\sum _{j=i+1}^{n}\left|a_{ij}\right |.$

Observera att $u_{n}$ alltid är noll och att den högra sidan av gränsen ovan är $\infty$ när en eller flera av konstanterna $u_{i}$ är en.

Snävare gränser för inversen av en WCDD L-matris är kända.

Ansökningar

På grund av deras förhållande till M-matriser (se ovan ) förekommer WCDD-matriser ofta i praktiska tillämpningar. Ett exempel ges nedan.

Monotona numeriska scheman

WCDD L-matriser uppstår naturligt från monotona approximationsscheman för partiella differentialekvationer .

Tänk till exempel på det endimensionella Poisson-problemet

$u^{\prime \prime }(x)+g(x)=0$ för $\displaystyle x\in (0, 1)}$

med Dirichlets gränsvillkor $u(0)=u(1)=0$ . Låter $\{0,h,2h,\ldots ,1\}$ vara ett numeriskt rutnät (för vissa positiva $h$ som delar enhet), en monotont ändligt skillnadsschema för Poisson-problemet har formen av

$-{\frac {1}{h^{2}}}A{\vec {u}}+{\vec {g}}=0$ där $[{\vec {g}}]_{j}=g(jh)$

och

$A={\begin{pmatrix}2&-1\\-1&2&-1\\&-1&2&-1\\&&\ddots &\ddots &\ddots \\&&&-1&2&-1\\&&&&-1&2 \end{pmatrix}}.$

Observera att $A$ är en WCDD L-matris.