Stränggjorda jord

Visualisering som visar att längden som läggs till omkretsen (blå) bara beror på den extra radien (röd) och inte den ursprungliga omkretsen (grå)

String girdling Earth är ett matematiskt pussel med en kontraintuitiv lösning. I en version av detta pussel är snöret hårt virat runt ekvatorn på en perfekt sfärisk jord. Om strängen skulle höjas 1 meter (3 fot 3 tum) från marken, hela vägen längs ekvatorn, hur mycket längre skulle strängen vara?

Alternativt skarvas 1 meter (3 fot 3 tum) snöre in i originalsträngen och den förlängda strängen omarrangeras så att den är på en enhetlig höjd över ekvatorn. Frågan som då ställs är om gapet mellan snöret och jorden kommer att tillåta passage av en bil, en katt eller ett tunt knivblad.

Lösning

Visuell analog med en kvadrat

Eftersom strängen måste höjas längs hela 40 000 km (25 000 mi) omkrets, kan man förvänta sig flera kilometer extra sträng. Överraskande nog är svaret 2 π eller runt 6,3 meter (21 fot).

I den andra frasen, med tanke på att 1 meter (3 fot 3 tum) är nästan försumbar jämfört med 40 000 km (25 000 mi) omkrets, kan det första svaret vara att den nya positionen för strängen inte kommer att skilja sig från den ursprungliga ytan- kramande position. Svaret är att en katt lätt kommer att passera genom gapet, vars storlek kommer att vara ) 1/2 . π meter eller cirka 16 cm (6,3 tum

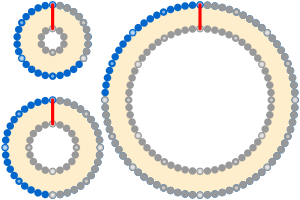
Ännu mer överraskande är att storleken på sfären eller cirkeln runt vilken strängen spänns är irrelevant, och kan vara allt från storleken på en atom till Vintergatan - resultatet beror bara på hur mycket den höjs. Dessutom, som i myntrullningsproblemet , behöver formen på stränggördlarna inte vara en cirkel: 2 π gånger förskjutningen läggs till när det är en enkel polygon eller sluten kurva som inte skär sig själv. Om formen är komplex måste 2 π gånger offset, gånger det absoluta värdet av dess vridningstal adderas.

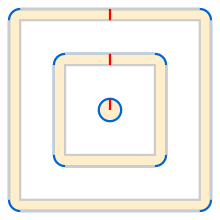
Detta diagram ger en visuell analog med hjälp av en kvadrat: oavsett kvadratens storlek är den adderade omkretsen summan av de fyra blå bågarna, en cirkel med samma radie som offseten.

Mer formellt, låt c vara jordens omkrets, r dess radie, Δc den adderade stränglängden och Δr den adderade radien. Eftersom en cirkel med radien R   har en omkrets av 2 π R ,

{{{annotations}}}

Fotografi som visar förskjutningen mellan startlinjerna på en friidrottsbana

${\begin{ aligned}c+\varDelta c&=2\pi (r+\varDelta r)\\2\pi r+\varDelta c&=2\pi r+2\pi \varDelta r\\\varDelta c&=2\pi \varDelta r\ \\därför \;\varDelta r&={\frac {\varDelta c}{2\pi }}\end{aligned}}$

oavsett värdet av c .

Denna observation innebär också att en friidrottsbana har samma förskjutning mellan startlinjerna på varje bana, lika med 2 π gånger banans bredd, oavsett om arenan är standard på 400 m (1 300 fot) eller storleken på en galax.

Se även

• Visuell kalkyl , ett intuitivt sätt att lösa den här typen av problem , användes ursprungligen för att hitta arean av en annulus , endast givet dess ackordlängd
• Servettringproblem , ett annat problem där radien på en sfär är kontraintuitivt irrelevant