Spricktillväxtekvation

Figur 1: Typisk plot av spricktillväxthastighet kontra spänningsintensitetsintervallet. Paris -Erdogan-ekvationen passar den centrala linjära regionen i Regim B.

En spricktillväxtekvation används för att beräkna storleken på en utmattningsspricka som växer från cykliska belastningar. Tillväxten av utmattningssprickor kan resultera i katastrofala fel, särskilt när det gäller flygplan. En ekvation av spricktillväxt kan användas för att säkerställa säkerheten, både i designfasen och under drift, genom att förutsäga sprickornas storlek. I kritisk struktur kan belastningar registreras och användas för att förutsäga storleken på sprickor för att säkerställa att underhåll eller återställning sker innan någon av sprickorna misslyckas.

Utmattningslivet kan delas in i en initieringsperiod och en spricktillväxtperiod. Spricktillväxtekvationer används för att förutsäga sprickstorleken med utgångspunkt från en given initial brist och baseras vanligtvis på experimentella data som erhållits från utmattningstest med konstant amplitud .

En av de tidigaste spricktillväxtekvationerna baserad på spänningsintensitetsfaktorområdet för en belastningscykel ( ${\displaystyle \Delta K} )$ är Paris–Erdogan-ekvationen

${da \over dN}=C(\Delta K)^{m}$

där $a$ är spricklängden och ${\rm {d}}a/{\rm {d}}N$ är utmattningsspricktillväxten för en enskild belastningscykel ${ \displaystyle N}$ . En mängd olika ekvationer för spricktillväxt som liknar Paris-Erdogan-ekvationen har utvecklats för att inkludera faktorer som påverkar spricktillväxthastigheten såsom spänningsförhållande, överbelastningar och effekter på belastningshistoriken.

Spänningsintensitetsintervallet kan beräknas från den maximala och lägsta spänningsintensiteten för en cykel

$\Delta K=K_{\text{max}}-K_{\text{min}}$

En geometrifaktor $\beta$ används för att relatera fjärrfältsspänningen $\sigma$ till sprickspetsens spänningsintensitet med hjälp av

$K=\beta \sigma {\sqrt {\pi a}}$ .

Det finns standardreferenser som innehåller geometrifaktorerna för många olika konfigurationer.

Historia om ekvationer för sprickutbredning

Många ekvationer för sprickutbredning har föreslagits under åren för att förbättra prediktionsnoggrannheten och införliva en mängd olika effekter. Verken av Head, Frost och Dugdale, McEvily och Illg och Liu om utmattningssprickor-tillväxtbeteende lade grunden i detta ämne. Den allmänna formen av dessa sprickutbredningsekvationer kan uttryckas som

${da \over dN}=f(\Delta \sigma ,a,C_{i}),$

där spricklängden betecknas med $a$ , antalet cykler av applicerad belastning ges av ${\displaystyle N} ,$ spänningsintervallet med $\Delta \sigma$ , och materialet parametrar av $C_{i}$ . För symmetriska konfigurationer definieras sprickans längd från symmetrilinjen som $a$ och är hälften av den totala spricklängden $2a$ .

Spricktillväxtekvationer av formen $da/dN$ är inte en sann differentialekvation eftersom de inte modellerar processen för spricktillväxt på ett kontinuerligt sätt under hela laddningscykeln. Som sådan, separata cykelräknings- eller identifieringsalgoritmer som den vanligaste algoritmen för regnflödesräkning , krävs för att identifiera maximi- och minimivärdena i en cykel. Även om det är utvecklat för metoderna för stress/töjningstid har regnflödesräkning också visat sig fungera för spricktillväxt. Det har funnits ett litet antal äkta derivatutmattningsspricktillväxtekvationer som också har utvecklats.

Faktorer som påverkar spricktillväxthastigheten

Regimer

Figur 1 visar en typisk kurva över hastigheten för spricktillväxt som en funktion av den alternerande spänningsintensiteten eller sprickspetsens drivkraft $\Delta K$ plottad på logskalor. Spricktillväxtens beteende med avseende på den alternerande stressintensiteten kan förklaras i olika regimer (se figur 1) enligt följande

Regim A: Vid låga tillväxthastigheter har variationer i mikrostruktur , medelspänning (eller belastningsförhållande) och miljö betydande effekter på sprickutbredningshastigheten. Det observeras vid låga belastningsförhållanden att tillväxthastigheten är mest känslig för mikrostruktur och i låghållfasta material är den mest känslig för belastningsförhållande.

Regim B: Vid medelstora tillväxthastigheter har variationer i mikrostruktur, medelspänning (eller belastningsförhållande), tjocklek och miljö inga signifikanta effekter på sprickutbredningshastigheten.

Regim C: Vid höga tillväxthastigheter är sprickutbredning mycket känslig för variationerna i mikrostruktur, medelspänning (eller belastningsförhållande) och tjocklek. Miljöeffekter har relativt sett mycket mindre inflytande.

Stressförhållande effekt

Cykler med högre spänningsförhållande $R=K_{\text{min}}}/{K_{\text{max}}\equiv P_{\text{min }}/{P_{\text{max}}}$ har en ökad hastighet av spricktillväxt. Denna effekt förklaras ofta med sprickförslutningskonceptet som beskriver observationen att sprickytorna kan förbli i kontakt med varandra vid belastningar över noll. Detta minskar det effektiva spänningsintensitetsfaktorområdet och tillväxthastigheten för utmattningssprickor.

Sekvenseffekter

En $da/dN$ -ekvation ger tillväxthastigheten för en enstaka cykel, men när belastningen inte är konstant amplitud kan förändringar i belastningen leda till tillfälliga ökningar eller minskningar i tillväxthastigheten. Ytterligare ekvationer har utvecklats för att hantera några av dessa fall. Tillväxthastigheten fördröjs när en överbelastning inträffar i en belastningssekvens. Dessa belastningar genererar en plastzon som kan fördröja tillväxttakten. Två anmärkningsvärda ekvationer för att modellera förseningarna som uppstår när sprickan växer genom överbelastningsområdet är:

Wheeler-modellen (1972)

$\left({\frac {da}{dN}}\right)_{\text{VA}}= \beta \left({\frac {da}{dN}}\right)_{\text{CA}}$ med $\beta =\left({\frac { r_{\text{pi}}}{r_{\text{max}}}}\höger)^{k}$

där $r_{\text{pi}}$ är plastzonen som motsvarar den i:te cykeln som inträffar efter överbelastningen och $r_{\text{max}}$ är avståndet mellan sprickan och omfattningen av plastzonen vid överbelastningen.

Willenborgsmodellen

Spricktillväxtekvationer

Tröskelekvation

För att förutsäga spricktillväxthastigheten vid området nära tröskeln har följande relation använts

${da \over dN}=A\left(\Delta K-\Delta K_{\text{th}}\right)^{p}.$

Paris–Erdoğan ekvation

För att förutsäga spricktillväxthastigheten i den mellanliggande regimen används Paris–Erdoğan-ekvationen

${da \over dN}=C\left(\Delta K\right)^{m}.$

Forman ekvation

1967 föreslog Forman följande relation för att ta hänsyn till de ökade tillväxthastigheterna på grund av spänningsförhållandet och när man närmade sig brottsegheten K $\displaystyle K_{\text{c}}}$

${da \over dN}={\frac {C(\Delta K)^{n}}{(1- R)K_{\text{c}}-\Delta K}}$

McEvily–Groeger ekvation

McEvily och Groeger föreslog följande makt-lagsförhållande som beaktar effekterna av både höga och låga värden på $\Delta K$

${da \over dN}=A(\Delta K-\Delta K_{\text{th }})^{2}{\Big [}1+{\frac {\Delta K}{K_{\text{Ic}}-K_{\text{max}}}}{\Big ]}$ .

NASGRO ekvation

NASGRO-ekvationen används i spricktillväxtprogrammen AFGROW, FASTRAN och NASGRO. Det är en generell ekvation som täcker den lägre tillväxthastigheten nära tröskeln $\Delta K_{\text{th}}$ och den ökade tillväxthastigheten som närmar sig brottsegheten $K_{\text{ crit}}$ , samt tillåta medelspänningseffekten genom att inkludera stressförhållandet $R$ . NASGRO-ekvationen är

${\frac {da}{dN}}=C\left[\left({\frac {1-f}{1-R}}\right)\Delta K\right]^{n}{\ vänster(1-{\frac {\Delta K_{\text{th}}}{\Delta K}}\höger)^{p} \över \left(1-{\frac {K_{\max }}{ K_{\text{crit}}}}\right)^{q}}$

där $C$ , $f$ , $n$ , $p$ , $q$ , $\Delta K_{\text{th }}$ och $K_{\text{crit}}$ är ekvationskoefficienterna.

McClintocks ekvation

1967 utvecklade McClintock en ekvation för den övre gränsen för spricktillväxt baserad på den cykliska sprickspetsens öppningsförskjutning $\Delta {\text{CTOD}}$

${da \over dN}\propto \Delta {\text{CTOD}}\approx \beta {(\Delta K)^{ 2} \över {2\sigma _{0}E'}}$

där $\sigma _{0}$ är flödesspänningen, $E'$ är Youngs modul och $\beta$ är en konstant typiskt i intervallet 0,1–0,5.

Walkers ekvation

För att ta hänsyn till stressförhållandeeffekten föreslog Walker en modifierad form av Paris-Erdogan-ekvationen

${da \over dN}=C{\Big (}{\overline {\Delta K}}{\Big )}^{m}=C{\bigg (}{\frac {\Delta K}{ (1-R)^{1-\gamma }}}{\bigg )}^{m}=C{\big (}K_{\text{max}}(1-R)^{\gamma }{\ stor )}^{m}$

där $\gamma$ är en materialparameter som representerar påverkan av spänningsförhållandet på tillväxthastigheten för utmattningssprickor. Vanligtvis $\gamma$ ett värde runt $0,5$ , men kan variera mellan $0,3-1,0$ . Generellt sett antas det att komprimerande del av belastningscykeln ${\big (}R<0{\big )}$ inte har någon effekt på spricktillväxten genom att beakta $\gamma =0,$ vilket ger ${\overline {\Delta K}}=K_{\text{max}}.$ Detta kan förklaras fysiskt genom att tänka på att sprickan stänger vid noll belastning och inte beter sig som en spricka under tryckbelastning. I mycket sega material som Man-Ten stål bidrar tryckbelastning till spricktillväxten enligt $\gamma =0,22$ .

Elbers ekvation

Elber modifierade Paris–Erdogan-ekvationen för att möjliggöra sprickstängning med införandet av öppningsspänningsintensitetsnivån K $\displaystyle K_{\text{op}}}$ vid vilken kontakt inträffar. Under denna nivå finns ingen rörelse vid sprickspetsen och därmed ingen tillväxt. Denna effekt har använts för att förklara stressförhållandeeffekten och den ökade tillväxthastigheten som observerats med korta sprickor. Elbers ekvation är

$\Delta K_{\text{eff}}=K_{\text{max}}-K_{\text{op}}$

${da \over dN}=C(\Delta K_{\text{eff}})^{m}$

Ekvation för sega och spröda material

Den allmänna formen av utmattningsspricktillväxthastigheten i sega och spröda material ges av

${da \over dN}\propto (K_{\text{max}})^{n}(\Delta K)^{p} ,$

där $n$ och $p$ är materialparametrar. Baserat på olika sprickförskjutnings- och sprickspetsskärmningsmekanismer i metaller, keramer och intermetaller , observeras att utmattningsspricktillväxthastigheten i metaller är signifikant beroende av $\Delta K$ term, i keramik på $K_{\text{max}}$ , och intermetallics har nästan liknande beroende av $\Delta K$ och $K_{\text{max}}$ termer.

Förutsägelse av trötthetsliv

Datorprogram

Det finns många datorprogram som implementerar spricktillväxtekvationer som Nasgro , AFGROW och Fastran . Dessutom finns det också program som implementerar ett probabilistiskt tillvägagångssätt för spricktillväxt som beräknar sannolikheten för fel under en komponents livslängd.

Spricktillväxtprogram växer en spricka från en initial briststorlek tills den överstiger brottsegheten hos ett material och misslyckas. Eftersom brottsegheten beror på randvillkoren kan brottsegheten ändras från plana töjningsförhållanden för en halvcirkulär ytspricka till plana spänningsförhållanden för en genomgående spricka. Brottsegheten för planspänningsförhållanden är typiskt dubbelt så stor som den för plan töjning. Men på grund av den snabba tillväxttakten för en spricka nära slutet av dess livslängd, förändrar variationer i brottseghet inte nämnvärt livslängden för en komponent.

Spricktillväxtprogram ger vanligtvis ett urval av:

• cykelräkningsmetoder för att extrahera cykelextremer
• geometrifaktorer som väljer sprickans form och den applicerade belastningen
• ekvation för spricktillväxt
• accelerations-/retardationsmodeller
• materialegenskaper som sträckgräns och brottseghet

Analytisk lösning

Stressintensitetsfaktorn ges av

$K=\beta \sigma {\sqrt {\pi a}},$

där $\sigma$ är den applicerade enhetliga dragspänningen som verkar på provet i riktningen vinkelrät mot sprickplanet, $a$ är spricklängden och $\beta$ är en dimensionslös parameter som beror på geometrin på provet. Den alternerande stressintensiteten blir

${\begin{aligned}\Delta K&={\begin{cases }\beta (\sigma _{\text{max}}-\sigma _{\text{min}}){\sqrt {\pi a}}=\beta \Delta \sigma {\sqrt {\pi a} },\qquad R\geq 0\\\beta \sigma _{\text{max}}{\sqrt {\pi a}},\qquad R<0\end{cases}},\end{aligned}}$

där $\Delta \sigma$ är intervallet för den cykliska spänningsamplituden.

Genom att anta att den initiala sprickstorleken är ${\displaystyle a_{0}} kan$ den kritiska sprickstorleken $a_{c}$ innan provet misslyckas beräknas med hjälp av ${ \displaystyle {\big (}K=K_{\text{max}}=K_{\text{Ic}}{\big )}}$ som

${\begin{aligned}K_{\text{Ic}}&=\beta \sigma _{\text{max}}{\sqrt {\pi a_{c}}},\\\Rightarrow a_{ c}&={\frac {1}{\pi }}{\bigg (}{\frac {K_{\text{Ic}}}{\beta \sigma _{\text{max}}}}{\ bigg )}^{2}.\end{aligned}}$

Ovanstående ekvation i $a_{c}$ är implicit till sin natur och kan lösas numeriskt om det behövs.

Fall I

För $R\geq 0,7,$ sprickförslutning en försumbar effekt på spricktillväxthastigheten och Paris–Erdogan-ekvationen kan användas för att beräkna utmattningslivslängden för ett prov innan det når den kritiska $a_{c}$ som

${\begin{aligned}{da \over dN}&=C(\Delta K)^{m}=C{\bigg (}\beta \Delta \sigma {\sqrt {\pi a}}{ \bigg )}^{m},\\\Rightarrow N_{f}&={\frac {1}{({\sqrt {\pi }}\Delta \sigma )^{m}}}\int _{ a_{0}}^{a_{c}}{\frac {da}{(C{\sqrt {a}}\beta )^{m}}}.\end{aligned}}$

Spricktillväxtmodell med konstant värde på 𝛽 och R = 0

Figur 2: Geometrisk representation av provexemplar av centrumsprickad spänning

För Griffith-Irwin spricktillväxtmodell eller mittspricka med längd $2a$ i ett oändligt ark som visas i figur 2, har vi $\beta =1$ och är oberoende av sprickan längd. Dessutom $C$ anses vara oberoende av spricklängden. Genom att anta $\beta ={\text{konstant}},$ förenklas ovanstående integral till

$N_{f}={\frac {1}{C({\sqrt {\pi }}\beta \Delta \sigma )^{m}}}\int _{a_{0}}^{a_{c}}{\frac {da}{({\sqrt {a}})^{m}}},$

genom att integrera uttrycket ovan för $m\neq 2$ och ${\displaystyle m=2} fall,$ ges det totala antalet belastningscykler ${\displaystyle N_{f}} av$

${\begin{aligned}N_{f}&={\frac {2}{(m-2)C({\sqrt {\pi }}\beta \Delta \sigma )^{m}}}{\Bigg [}{\frac {1}{(a_{0})^{\frac {m-2}{2}}}}-{\frac {1 }{(a_{c})^{\frac {m-2}{2}}}}{\Bigg ]},\qquad m\neq 2,\\N_{f}&={\frac {1} {\pi C(\beta \Delta \sigma )^{2}}}\ln {\frac {a_{c}}{a_{0}}},\qquad m=2.\end{aligned}}$

Nu, för $m>2$ och kritisk sprickstorlek är mycket stor i jämförelse med den ursprungliga sprickstorleken ( $\displaystyle {\big (}a_{c}>>a_ {0}{\big )}}$ kommer att ge

$N_{f}={\frac {2}{(m-2)C({\sqrt {\pi }}\Delta \sigma \beta )^{m}}}(a_{0})^ {\frac {2-m}{2}}.$

Ovanstående analytiska uttryck för det totala antalet belastningscykler till brott ( $\displaystyle {\big (}N_{f}{\big )}}$ erhålls genom att anta $Y={\text {konstant}}$ . I de fall där $\beta$ är beroende av sprickstorleken, såsom Single Edge Notch Tension (SENT), Center Cracked Tension (CCT) geometrier, kan numerisk integration användas för att beräkna $N_ {f}$ .

Fall II

För $R<0,7,$ har sprickförslutningsfenomen en effekt på spricktillväxthastigheten och vi kan åberopa Walker-ekvationen för att beräkna utmattningslivslängden för ett prov innan det når den kritiska sprickstorleken a c $displaystyle a_{c}}$ som

${\begin{aligned}{da \over dN}&=C{\bigg (}{\frac {\Delta K}{(1-R)^{1-\gamma }}}{\bigg) }^{m}={\frac {C}{(1-R)^{m(1-\gamma )}}}{\bigg (}\beta \Delta \sigma {\sqrt {\pi a}} {\bigg )}^{m},\\\Rightarrow N_{f}&={\frac {(1-R)^{m(1-\gamma )}}{({\sqrt {\pi }} \Delta \sigma )^{m}}}\int _{a_{0}}^{a_{c}}{\frac {da}{(C{\sqrt {a}}\beta )^{m} }}.\end{aligned}}$

Numerisk beräkning

Figur 3: Schematisk representation av förutsägelseprocess för utmattningsliv

Detta schema är användbart när $\beta$ är beroende av sprickstorleken $a$ . Den initiala sprickstorleken anses vara $a_{0}$ . Spänningsintensitetsfaktorn vid den aktuella sprickstorleken $a$ beräknas med den maximala applicerade spänningen som

${\begin{aligned}K_{\text{max}}&=\beta \sigma _{\text{max}}{\sqrt {\pi a}}.\end{aligned}}$ Om $K_{\text{max}}$ är mindre än brottsegheten $K_{\text{Ic}}$ , sprickan har inte nått sin kritiska storlek $a_{c }$ och simuleringen fortsätter med den aktuella sprickstorleken för att beräkna den alternerande spänningsintensiteten som

$\Delta K=\beta \Delta \sigma {\sqrt {\pi a}}.$

Nu, genom att ersätta spänningsintensitetsfaktorn i Paris–Erdogan-ekvationen, beräknas ökningen av sprickstorleken ${\displaystyle \Delta a} som$

$\Delta a=C(\Delta K)^{m}\Delta N,$

där $\Delta N$ är cykelstegstorlek. Den nya sprickstorleken blir

$a_{i+1}=a_{i}+\Delta a,$

där index $i$ refererar till det aktuella iterationssteget. Den nya sprickstorleken används för att beräkna spänningsintensiteten vid maximal applicerad spänning för nästa iteration. Denna iterativa process fortsätter tills

$K_{\text{max}}\geq K_{\text{Ic}}.$

När detta felkriterium är uppfyllt stoppas simuleringen.

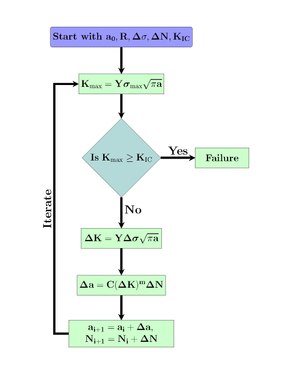
Den schematiska representationen av förutsägelseprocessen för utmattningsliv visas i figur 3.

Exempel

Figur 4: Geometrisk representation av Single Edge Notch Tension-testprov

Spänningsintensitetsfaktorn i ett SENT-prov (se figur 4) under utmattningsspricktillväxt ges av

${\begin{aligned}K_{I}&=\beta \sigma {\sqrt {\pi a}}=\sigma {\sqrt {\pi a}}{\Bigg [}0,265{\bigg [ }1-{\frac {a}{W}}{\bigg ]}^{4}+{\frac {0.857+0.265{\frac {a}{W}}}{{\big [}1-{ \frac {a}{W}}{\big ]}^{\frac {3}{2}}}}{\Bigg ]},\\\Delta K_{I}&=K_{\text{max} }-K_{\text{min}}=\beta \Delta \sigma {\sqrt {\pi a}}.\end{aligned}}$

Följande parametrar beaktas för beräkningen

$a_{0}=5$ mm, $W=100$ mm, $h=200$ mm, ${\displaystyle K_{ \text{Ic}}=30{\text{ MPa}}{\sqrt {\text{m}}}} ,$ R $\displaystyle R={\frac {K_{\text{ min}}}{K_{\text{max}}}}=0.7}$ ,

$\Delta \sigma =20$ MPa, $C=4,6774\times 10^{-11}{\frac {\ text{m}}{\text{cykel}}}{\frac {1}{({\text{MPa}}{\sqrt {\text{m}}})^{m}}}$ , $m=3.874$ .

Den kritiska spricklängden, $a=a_{c}$ , kan beräknas när $K_{\text{max}}=K_{\text{Ic}}$ som

$a_{c}={\frac {1}{\pi }}{\Bigg (}{\frac {0.45}{\beta }}{\Bigg )}^{2}.$

Genom att lösa ovanstående ekvation erhålls den kritiska spricklängden som $a_{c}=26,7{\text{mm}}$ .

Att nu åberopa Paris–Erdogan-ekvationen ger

$N_{f}={\frac {1}{C(\Delta \sigma )^{m}({\sqrt {\pi }})^{m}}}\int _{a_{0} }^{a_{c}}{\frac {da}{a^{\frac {m}{2}}{\Bigg [}0,265{\bigg [}1-{\frac {a}{W}} {\bigg ]}^{4}+{\frac {0.857+0.265{\frac {a}{W}}}{{\big [}1-{\frac {a}{W}}{\big ] }^{\frac {3}{2}}}}{\Bigg ]}^{m}}}$

Genom numerisk integration av uttrycket ovan erhålls det totala antalet belastningscykler till fel som $N_{f}=1,2085\x 10^{6}{\text{ cykler$ .

externa länkar

• Forman, RG; Shivakumar, V.; Cardinal, JW; Williams, LC; McKeighan, PC (2005). "Fatigue Crack Growth Database for Damage Tolerance Analysis" (PDF) . FAA . Hämtad 6 juli 2019 .
• Gallagher, JP; Giessler, FJ; Berens, AP; Engle, Jr, JM "USAF Damage Tolerant Design Handbook: Guidelines for the Analysis and Design of Damage Tolerant Aircraft Structures. Revision B" . Arkiverad från originalet den 9 juli 2019 . Hämtad 9 juli 2019 .
• "Handbok för utvärdering av skadetolerans, volym I: Introduktion, frakturmekanik, utmattningssprickförökning" ( PDF) . Federal Aviation Administration. 1993 . Hämtad 16 juli 2019 .