Sorterad array

Sorterad array
Sorterad array
Typ	Array
Uppfunnet	1945
Uppfunnet av	John von Neumann
Tidskomplexitet i stor O-notation
Algoritm
Algoritm	Genomsnitt
Plats	På)
Sök	O(log n)
Föra in	På)
Radera	På)

En sorterad array är en array-datastruktur där varje element sorteras i numerisk, alfabetisk eller någon annan ordning och placeras på lika åtskilda adresser i datorns minne. Det används vanligtvis inom datavetenskap för att implementera statiska uppslagstabeller för att hålla flera värden som har samma datatyp . Att sortera en array är användbart för att organisera data i ordnad form och snabbt återställa dem.

Metoder

Det finns många välkända metoder för att sortera en array, vilka inkluderar, men är inte begränsade till: Urvalssortering , Bubblesortering , Infogningssortering , Sammanfogad sortering , Snabbsortering , Heapsortering och Räknesortering . ^{[ citat behövs ]} Dessa sorteringstekniker har olika algoritmer förknippade med dem, och det finns därför olika fördelar med att använda varje metod.

Översikt

Sorterade arrayer är den mest utrymmeseffektiva datastrukturen med den bästa referensplatsen för sekventiellt lagrad data. ^{[ citat behövs ]}

Element inom en sorterad array hittas med en binär sökning , i O(log n ); sålunda är sorterade arrayer lämpade för fall då man behöver kunna slå upp element snabbt, t.ex. som en uppsättning eller multiset datastruktur . Denna komplexitet för uppslagningar är densamma som för självbalanserande binära sökträd .

I vissa datastrukturer används en rad strukturer. I sådana fall kan samma sorteringsmetoder användas för att sortera strukturerna enligt någon nyckel som ett strukturelement; t.ex. sortering av elevernas register efter rullnummer eller namn eller betyg.

Om man använder en sorterad dynamisk array är det möjligt att infoga och ta bort element. Infogning och borttagning av element i en sorterad array körs vid O( n ), på grund av behovet av att flytta alla element efter det element som ska infogas eller tas bort; i jämförelse infogar och raderar ett självbalanserande binärt sökträd vid O(log n ). I det fall då element tas bort eller infogas i slutet, kan en sorterad dynamisk array göra detta på avskriven O(1)-tid medan ett självbalanserande binärt sökträd alltid fungerar vid O(log n ).

Element i en sorterad array kan slås upp efter deras index ( random access ) vid O(1) tid, en operation som tar O(log n ) eller O( n ) tid för mer komplexa datastrukturer.

Historia

John von Neumann skrev det första arraysorteringsprogrammet ( merge sort ) 1945, när den första lagrade programdatorn fortfarande byggdes.

Tillämpningar av sorterade arrayer

Kommersiell datoranvändning

Statliga organisationer, privata företag och många webbaserade applikationer måste hantera enorma mängder data. Uppgifterna måste ofta nås flera gånger. Att hålla data i ett sorterat format möjliggör snabb och enkel hämtning.

I diskret matematik

Sorterade arrayer kan användas för att implementera Dijkstras algoritm eller Prims algoritm . Även algoritmer som Kruskals algoritm för att hitta minimala spännträd.

I prioriterad schemaläggning

På operativsystemnivå är många processer väntande åt gången, men de kan bara hantera en process i en instans i tiden. Därför är prioriteringar kopplade till varje process. Sedan skickas processerna till CPU:n enligt högsta prioritet genom att använda sorterade process-ID:n. Här sorterades processer beroende på deras prioriteringar och sedan allokeras CPU till dem. Processen som har högst prioritet tar första positionen i sorterad array. Därför görs schemaläggning av systemprocesser prioriterat.

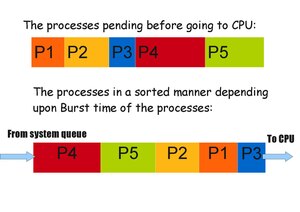
I kortaste-jobb-först schemaläggning

Detta är det speciella fallet med prioriteringsplanering. Här sorteras processer efter sprängtid för processerna. Processen som kräver den kortaste tiden kommer att tilldelas CPU först. Därför skickas processer till CPU enligt deras skurtid.

Bearbeta	Sprängtid
P1	3
P2	4
P3	1
P4	8
P5	6

Se även