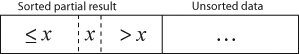Insättningssort

Insättningssort

Animation av insättningssort
Klass	Sorteringsalgoritm
Datastruktur	Array
Prestanda i värsta fall	$O(n^{2})$ jämförelser och byten
Bästa möjliga prestanda	$O(n)$ jämförelser, $O(1)$ swappar
Genomsnittlig prestanda	$O(n^{2})$ jämförelser och byten
Värsta tänkbara utrymmeskomplexitet	$O(n)$ totalt, $O(1)$ extra

Insättningssortering är en enkel sorteringsalgoritm som bygger den slutgiltiga sorterade matrisen (eller listan) ett objekt i taget genom jämförelser . Det är mycket mindre effektivt på stora listor än mer avancerade algoritmer som quicksort , heapsort eller merge sort . Insättningssortering ger dock flera fördelar:

• Enkel implementering: Jon Bentley visar en treradig C / C++ -version som är fem rader när den är optimerad .
• Effektiv för (ganska) små datamängder, ungefär som andra kvadratiska (dvs O ( n ² )) sorteringsalgoritmer
• Mer effektiv i praktiken än de flesta andra enkla kvadratiska algoritmer som urvalssortering eller bubbelsortering
• Adaptiv , dvs effektiv för datamängder som redan är väsentligen sorterade: tidskomplexiteten är O ( kn ) när varje element i inmatningen inte är mer än k platser bort från sin sorterade position
• Stabil ; dvs ändrar inte den relativa ordningen för element med lika nycklar
• På plats ; dvs kräver endast en konstant mängd O(1) extra minnesutrymme
• Online ; dvs kan sortera en lista när den tar emot den

När människor manuellt sorterar kort i en bridgehand använder de flesta en metod som liknar insättningssortering.

Algoritm

Ett grafiskt exempel på infogningssort. Den partiellt sorterade listan (svart) innehåller initialt endast det första elementet i listan. Med varje iteration tas ett element (rött) bort från "ännu ej kontrollerat för beställning" indata och infogas på plats i den sorterade listan.

Insättningssortering itererar , förbrukar ett inmatningselement varje upprepning och skapar en sorterad utdatalista. Vid varje iteration tar insättningssortering bort ett element från indata, hittar platsen det hör hemma i den sorterade listan och infogar det där. Det upprepas tills inga inmatningselement finns kvar.

Sortering görs vanligtvis på plats, genom att iterera upp arrayen, utöka den sorterade listan bakom den. Vid varje array-position kontrollerar den värdet där mot det största värdet i den sorterade listan (som råkar vara bredvid, i den föregående array-positionen kontrollerad). Om den är större lämnar den elementet på plats och flyttar till nästa. Om den är mindre, hittar den rätt position i den sorterade listan, flyttar alla större värden uppåt för att skapa ett mellanslag och infogar i den korrekta positionen.

Den resulterande matrisen efter k iterationer har egenskapen där de första k + 1-posterna sorteras ("+1" eftersom den första posten hoppas över). I varje iteration tas den första återstående inmatningen bort och infogas i resultatet på rätt position, vilket förlänger resultatet:

blir

med varje element större än x kopierat till höger när det jämförs med x .

Den vanligaste varianten av infogningssort, som fungerar på arrayer, kan beskrivas på följande sätt:

1. Anta att det finns en funktion som heter Insert utformad för att infoga ett värde i en sorterad sekvens i början av en array. Den fungerar genom att börja i slutet av sekvensen och flytta varje element en plats åt höger tills en lämplig position hittas för det nya elementet. Funktionen har som bieffekt att värdet som lagras omedelbart efter den sorterade sekvensen i arrayen skrivs över.
2. För att utföra en infogningssortering börjar du längst till vänster i arrayen och anropar Insert för att infoga varje element som påträffas i dess korrekta position. Den ordnade sekvensen i vilken elementet infogas lagras i början av arrayen i uppsättningen av index som redan undersökts. Varje infogning skriver över ett enda värde: värdet som infogas.

Pseudokoden för den kompletta algoritmen följer, där arrayerna är nollbaserade :

 i ← 1  medan  i < längd(A) j ← i  medan  j > 0  och  A[j-1] > A[j]  byter  A[j] och A[j-1] j ← j - 1  slut medan  i ← i + 1  slut medan 

Den yttre slingan löper över alla element utom det första, eftersom enkelelementsprefixet A[0:1] är trivialt sorterat, så invarianten som de första i -posterna sorteras är sann från början. Den inre slingan flyttar element A[i] till sin rätta plats så att efter slingan sorteras de första i+1 elementen. Observera att och -operatorn i testet måste använda kortslutningsutvärdering , annars kan testet resultera i ett array bounds error , när j=0 och den försöker utvärdera A[j-1] > A[j] (dvs. A[-1] misslyckas).

Efter att ha utökat bytesoperationen på plats som x ← A[j]; A[j] ← A[j-1]; A[j-1] ← x (där x är en temporär variabel), en något snabbare version kan produceras som flyttar A[i] till sin position på en gång och bara utför en tilldelning i den inre slingkroppen:

 i ← 1  medan  i < längd(A) x ← A[i] j ← i - 1  medan  j >= 0  och  A[j] > x A[j+1] ← A[j] j ← j - 1  slut medan  A[j+1] ← x i ← i + 1  slutar medan 

Den nya inre slingan flyttar element åt höger för att rensa en punkt för x = A[i] .

Algoritmen kan också implementeras på ett rekursivt sätt. Rekursionen ersätter bara den yttre slingan, anropar sig själv och lagrar successivt mindre värden på n i stacken tills n är lika med 0, där funktionen sedan returnerar uppåt i anropskedjan för att exekvera koden efter varje rekursivt anrop som börjar med n lika med 1, med n ökar med 1 när varje instans av funktionen återgår till den tidigare instansen. Det första anropet skulle vara insertionSortR(A, length(A)-1) .

 funktion  insertionSortR(array A, int n)  om  n > 0 insertionSortR(A, n-1) x ← A[n] j ← n-1  medan  j >= 0  och  A[j] > x A[j+1] ← A[j] j ← j-1  slut medan  A[j+1] ← x  slut om  slutfunktion 

Det gör inte koden kortare, det minskar inte heller exekveringstiden, men det ökar den extra minnesförbrukningen från O(1) till O(N) (på den djupaste nivån av rekursion innehåller stacken N referenser till En matris, var och en med tillhörande värde på variabel n från N ner till 1).

Bästa, värsta och genomsnittliga fall

Det bästa fallet är en array som redan är sorterad. I det här fallet har insättningssorteringen en linjär körtid (dvs O( n )). Under varje iteration jämförs det första återstående elementet i inmatningen endast med elementet längst till höger i den sorterade undersektionen av arrayen.

Den enklaste värsta inmatningen är en array sorterad i omvänd ordning. Uppsättningen av alla värsta ingångar består av alla arrayer där varje element är det minsta eller näst minsta av elementen före det. I dessa fall kommer varje iteration av den inre slingan att skanna och förskjuta hela den sorterade undersektionen av arrayen innan nästa element infogas. Detta ger insättningssorteringen en kvadratisk körtid (dvs O( n ² )).

Det genomsnittliga fallet är också kvadratiskt, vilket gör insättningssortering opraktisk för sortering av stora arrayer. Insättningssortering är dock en av de snabbaste algoritmerna för att sortera mycket små arrayer, till och med snabbare än quicksort ; faktiskt, bra quicksort- implementationer använder insättningssortering för arrayer som är mindre än en viss tröskel, även när de uppstår som underproblem; den exakta tröskeln måste bestämmas experimentellt och beror på maskinen, men är vanligtvis runt tio.

Exempel: Följande tabell visar stegen för att sortera sekvensen {3, 7, 4, 9, 5, 2, 6, 1}. I varje steg är den aktuella nyckeln understruken. Nyckeln som flyttades (eller lämnades på plats eftersom den var den största hittills) i föregående steg är markerad med en asterisk.

 3  7 4 9 5 2 6 1 3  *  7  4  9 5 2 6 1 3 7* 4 9 5 2 6 1 3 4* 7  9  5 2 6 1 3 4 7 9*  5  2 6 1 3 4 5* 7 9  2  6 1 2* 3 4 5 7 9  6  1 2 3 4 5 6* 7 9  1  1* 2 3 4 5 6 7 9 

Relation till andra sorteringsalgoritmer

Infogningssortering är mycket lik urvalssortering . Liksom i urvalssortering, efter att k passerat genom arrayen, är de första k elementen i sorterad ordning. Den grundläggande skillnaden mellan de två algoritmerna är dock att insättningssorteringen skannar bakåt från den aktuella nyckeln, medan urvalssorteringen skannar framåt. Detta resulterar i att urvalssorteringen gör de första k elementen till de k minsta elementen i den osorterade ingången, medan de vid insättningssortering helt enkelt är de första k elementen i inmatningen.

Den primära fördelen med infogningssortering framför urvalssortering är att urvalssortering alltid måste skanna alla återstående element för att hitta det absolut minsta elementet i den osorterade delen av listan, medan infogningssortering endast kräver en enda jämförelse när ( k + 1 ) -st elementet är större än det k -te elementet; när detta ofta är sant (t.ex. om inmatningsmatrisen redan är sorterad eller delvis sorterad), är insättningssorteringen klart mer effektiv jämfört med urvalssorteringen. I genomsnitt (förutsatt att rangordningen av ( k + 1)-st elementets rangordning är slumpmässig), kommer insättningssorteringen att kräva jämförelse och förskjutning av hälften av de tidigare k elementen, vilket innebär att infogningssortering kommer att utföra ungefär hälften så många jämförelser som urvalssortering på genomsnitt.

I värsta fall för infogningssortering (när inmatningsmatrisen är omvänd sorterad) utför infogningssorteringen lika många jämförelser som urvalssorteringen. En nackdel med insättningssortering över urvalssortering är dock att det kräver fler skrivningar på grund av det faktum att, vid varje iteration, att infoga ( k + 1)-st elementet i den sorterade delen av arrayen kräver många elementbyten för att skifta alla av följande element, medan endast ett enda byte krävs för varje iteration av urvalssort. I allmänhet kommer insättningssortering att skriva till arrayen O( n ² ) gånger, medan urvalssortering endast skriver O( n ) gånger. Av denna anledning kan valsortering vara att föredra i fall där skrivning till minnet är betydligt dyrare än läsning, till exempel med EEPROM eller flashminne .

Medan vissa dela-och-erövra-algoritmer som quicksort och mergesort överträffar insättningssorteringen för större arrayer, är icke-rekursiva sorteringsalgoritmer som infogningssortering eller urvalssortering i allmänhet snabbare för mycket små arrayer (den exakta storleken varierar beroende på miljö och implementering, men är vanligtvis mellan 7 och 50 element). Därför är en användbar optimering i implementeringen av dessa algoritmer en hybridmetod som använder den enklare algoritmen när arrayen har delats upp till en liten storlek.

Varianter

DL Shell gjorde betydande förbättringar av algoritmen; den modifierade versionen heter Shell sort . Sorteringsalgoritmen jämför element åtskilda av ett avstånd som minskar vid varje pass. Shell sort har klart förbättrade gångtider i praktiskt arbete, med två enkla varianter som kräver O( n ^3/2 ) och O( n ^4/3 ) gångtid.

  Om kostnaden för jämförelser överstiger kostnaden för swappar, vilket till exempel är fallet med strängnycklar lagrade genom referens eller med mänsklig interaktion (som att välja en av ett par som visas sida vid sida), kan användning av binär infogningssortering ge resultat bättre prestanda. Binär infogningssortering använder en binär sökning för att bestämma den korrekta platsen för att infoga nya element, och utför därför ⌈log ₂ n ⌉ jämförelser i värsta fall. När varje element i arrayen söks efter och infogas är detta O( n log n ). Algoritmen som helhet har fortfarande en gångtid på O( n ² ) i genomsnitt på grund av den serie av byten som krävs för varje infogning.

Antalet byten kan minskas genom att beräkna positionen för flera element innan de flyttas. Till exempel, om målpositionen för två element beräknas innan de flyttas till rätt position, kan antalet byten minskas med cirka 25 % för slumpmässiga data. I extremfallet fungerar den här varianten på samma sätt som merge sort .

En variant som heter binär sammanfogad sortering använder en binär infogningssortering för att sortera grupper om 32 element, följt av en slutlig sortering med merge sort . Den kombinerar hastigheten för infogningssortering på små datamängder med hastigheten för sammanslagningssortering på stora datamängder.

För att undvika att behöva göra en serie byten för varje infogning, kan indata lagras i en länkad lista , vilket gör att element kan skarvas in i eller ut ur listan i konstant tid när positionen i listan är känd. Att söka i en länkad lista kräver dock att man följer länkarna till önskad position i följd: en länkad lista har inte slumpmässig åtkomst, så den kan inte använda en snabbare metod som binär sökning. Därför är den löptid som krävs för sökning O( n ), och tiden för sortering är O( n ² ). Om en mer sofistikerad datastruktur (t.ex. heap eller binärt träd ) används, kan tiden som krävs för sökning och infogning reduceras avsevärt; detta är kärnan i högsortering och binär trädsortering .

2006 publicerade Bender, Martin Farach-Colton och Mosteiro en ny variant av infogningssortering som kallas bibliotekssortering eller gapped insertion sort som lämnar ett litet antal oanvända utrymmen (dvs "luckor") utspridda över hela arrayen. Fördelen är att insättningar bara behöver flytta över element tills ett gap nås. Författarna visar att denna sorteringsalgoritm körs med hög sannolikhet i O( n log n ) tid.

Om en överhoppningslista används sänks insättningstiden till O(log n ), och byten behövs inte eftersom överhoppningslistan är implementerad på en länkad liststruktur. Den slutliga körtiden för infogning skulle vara O( n log n ).

Lista infogningssorteringskod i C

Om objekten är lagrade i en länkad lista kan listan sorteras med O(1) extra utrymme. Algoritmen börjar med en initialt tom (och därför trivialt sorterad) lista. Inmatningsobjekten tas bort från listan en i taget och infogas sedan på rätt plats i den sorterade listan. När inmatningslistan är tom får den sorterade listan önskat resultat.

       

    
           
         
    
         
        
             
          
                
            
            
              
              
          
            
                 
                
                     
                       
                
                    
                      
                      
                     
                
                  
            
        
    
     
 struct  LIST  *  SortList1  (  struct  LIST  *  pList  )  {  // noll eller ett element i listan  if  (  pList  ==  NULL  ||  pList  ->  pNext  ==  NULL  )  returnerar  pList  ;  // head är det första elementet i den resulterande sorterade  liststrukturen  LIST  *  head  =  NULL  ;  while  (  pList  !=  NULL  )  {  struct  LIST  *  current  =  pList  ;  pList  =  pList  ->  pNext  ;  if  (  head  ==  NULL  ||  aktuell  ->  iValue  <  head  ->  iValue  )  {  // infoga i huvudet på den sorterade listan  // eller som det första elementet i en tom sorterad lista  aktuell  ->  pNext  =  head  ;  huvud  =  ström  ;  }  else  {  // infoga aktuellt element i rätt position i icke-tom sorterad  liststruktur  LIST  *  p  =  head  ;  while  (  p  !=  NULL  )  {  if  (  p  ->  pNext  ==  NULL  ||  // sista elementet i den sorterade listan  aktuell  ->  iValue  <  p  ->  pNext  ->  iValue  )  // mitten av listan  {  // infoga i mitten av den sorterade listan eller som det sista elementet  aktuell  ->  pNext  =  p  ->  pNext  ;  p  ->  pNext  =  aktuell  ;  bryta  ;  // klar  }  p  =  p  ->  pNästa  ;  }  }  }  returnera  huvudet  ;  } 

Algoritmen nedan använder en avslutande pekare för infogning i den sorterade listan. En enklare rekursiv metod bygger om listan varje gång (istället för att splitsa) och kan använda O( n ) stackutrymme.

 

     
             


      

  
     
       

  
       

  
      
      
              
      
           

      
        

      
               
          
            
      

        
        
  

   
 struct  LIST  {  struct  LIST  *  pNext  ;  int  iValue  ;  };  struct  LIST  *  SortList  (  struct  LIST  *  pList  )  {  // noll eller ett element i listan  if  (  !  pList  ||  !  pList  ->  pNext  )  returnerar  pList  ;  /* bygg upp den sorterade arrayen från den tomma listan */  struct  LIST  *  pSorted  =  NULL  ;  /* ta objekt från inmatningslistan en efter en tills de är tomma */  while  (  pList  !=  NULL  )  {  /* kom ihåg huvudet */  struct  LIST  *  pHead  =  pList  ;  /* efterföljande pekare för effektiv skarvning */  struct  LIST  **  ppTrail  =  &  pSorted  ;  /* pop head off list */  pList  =  pList  ->  pNext  ;  /* skarva huvudet i sorterad lista på rätt plats */  while  (  !  (  *  ppTrail  ==  NULL  ||  pHead  ->  iValue  <  (  *  ppTrail  )  ->  iValue  ))  {  /* hör huvudet hemma här? */   /* nej - fortsätt ner i listan */  ppTrail  =  &  (  *  ppTrail  )  ->  pNext  ;  }  pHead  ->  pNext  =  *  ppTrail  ;  *  ppTrail  =  pH-huvud  ;  }  returnera  pSorted  ;  } 

Vidare läsning

•   Knuth, Donald (1998), "5.2.1: Sorting by Insertion", The Art of Computer Programming , vol. 3. Sortering and Searching (andra upplagan), Addison-Wesley, s. 80–105, ISBN 0-201-89685-0 .

externa länkar

• Animerade sorteringsalgoritmer: Insättningssortering vid Wayback Machine (arkiverad 8 mars 2015) – grafisk demonstration
• Adamovsky, John Paul, Binary Insertion Sort – Scoreboard – Complete Investigation and C Implementation , Pathcom .
• Insättningssortering – en jämförelse med andra O(n ² )-sorteringsalgoritmer , Storbritannien : Core war .
• Insertion sort (C) (wiki), LiteratePrograms – implementeringar av infogningssort i C och flera andra programmeringsspråk