Sekreterare problem

Grafer över sannolikheter för att få den bästa kandidaten (röda cirklar) från n ansökningar och k / n (blå kryss) där k är urvalsstorleken

Sekreterarproblemet visar ett scenario med optimal stoppteori som studeras flitigt inom områdena tillämpad sannolikhet , statistik och beslutsteori . Det är också känt som äktenskapsproblemet , sultanens hemgiftsproblem , det kinkiga friarproblemet , googolspelet och problemet med det bästa valet .

Den grundläggande formen av problemet är följande: föreställ dig en administratör som vill anställa den bästa sekreteraren av $n$ rankbara sökande till en tjänst. De sökande intervjuas en efter en i slumpmässig ordning. Beslut om varje enskild sökande ska fattas omedelbart efter intervjun. När den väl avvisats kan en sökande inte återkallas. Under intervjun får administratören tillräcklig information för att rangordna sökanden bland alla sökande som hittills intervjuats, men är omedveten om kvaliteten på ännu osynliga sökande. Frågan handlar om den optimala strategin ( stoppregeln ) för att maximera sannolikheten att välja den bästa sökanden. Om beslutet kan skjutas upp till slutet kan detta lösas genom den enkla maximala urvalsalgoritmen att spåra det löpande maximumet (och vem som uppnådde det) och välja det totala maximumet i slutet. Svårigheten är att beslutet måste fattas omedelbart.

Det kortaste rigorösa beviset hittills tillhandahålls av oddsalgoritmen . Det innebär att den optimala vinstsannolikheten alltid är minst $1/e$ (där e är basen för den naturliga logaritmen ), och att den senare gäller även i en mycket större generalitet. Den optimala stoppregeln föreskriver att alltid avvisa de första $\sim n/e$ sökande som intervjuas och sedan stanna vid den första sökande som är bättre än alla sökande som intervjuats hittills (eller fortsätta till den sista sökanden om detta händer aldrig). Ibland kallas denna strategi för $1/e$ , eftersom sannolikheten för att stanna vid den bästa sökanden med denna strategi är ungefär $1/e$ redan för måttliga värden på ${ \displaystyle n}$ . En anledning till att sekreterarproblemet har fått så mycket uppmärksamhet är att den optimala policyn för problemet (stoppregeln) är enkel och väljer ut den enskilt bästa kandidaten cirka 37 % av gångerna, oavsett om det finns 100 eller 100 miljoner sökande.

Formulering

Även om det finns många variationer kan det grundläggande problemet anges som följer:

• Det finns en enda tjänst att fylla.
• Det finns n sökande till tjänsten och värdet på n är känt.
• De sökande kan, om de ses sammantaget, otvetydigt rangordnas från bäst till sämst.
• De sökande intervjuas sekventiellt i slumpmässig ordning, där varje ordning är lika sannolik.
• Omedelbart efter en intervju antas eller avvisas den intervjuade sökanden och beslutet är oåterkalleligt.
• Beslutet att acceptera eller avslå en sökande kan endast baseras på den relativa rangen av de sökande som hittills intervjuats.
• Syftet med den allmänna lösningen är att ha störst sannolikhet att välja den bästa sökanden av hela gruppen. Detta är samma sak som att maximera den förväntade utdelningen, med utdelningen definierad som en för den bästa sökanden och noll annars.

En kandidat definieras som en sökande som vid intervju är bättre än alla tidigare intervjuade sökande. Skip används för att betyda "avvisa direkt efter intervjun". Eftersom målet i problemet är att välja den enskilt bästa sökanden, kommer endast kandidater att övervägas för antagning. "Kandidaten" i detta sammanhang motsvarar begreppet rekord i permutation.

Att ta fram den optimala politiken

Den optimala policyn för problemet är en stoppregel . Enligt den avslår intervjuaren de första r − 1 sökandena (låt sökande M vara den bästa sökanden bland dessa r − 1 sökande), och väljer sedan den första efterföljande sökanden som är bättre än sökande M . Det kan visas att den optimala strategin ligger i denna klass av strategier. (Observera att vi aldrig bör välja en sökande som inte är den bästa vi har sett hittills, eftersom de inte kan vara den bästa totala sökanden.) För en godtycklig cutoff r är sannolikheten att den bästa sökanden väljs ut.

${\begin{aligned}P(r)&=\sum _{i=1}^{n}P\left({\text{applicant }}i{\text{ är vald}}\cap { \text{sökande }}i{\text{ är bäst}}\right)\\&=\summa _{i=1}^{n}P\left({\text{sökande }}i{\text { är vald}}|{\text{sökande }}i{\text{ är bäst}}\right)\cdot P\left({\text{sökande }}i{\text{ är bäst}}\ höger)\\&=\left[\sum _{i=1}^{r-1}0+\sum _{i=r}^{n}P\left(\left.{\begin{array} {l}{\text{det bästa av de första }}i-1{\text{ sökanden}}\\{\text{är i den första }}r-1{\text{ sökanden}}\end{array }}\right|{\text{sökande }}i{\text{ är bäst}}\right)\right]\cdot {\frac {1}{n}}\\&=\left[\sum _ {i=r}^{n}{\frac {r-1}{i-1}}\right]\cdot {\frac {1}{n}}\\&={\frac {r-1} {n}}\summa _{i=r}^{n}{\frac {1}{i-1}}.\end{aligned}}$

Summan är inte definierad för r = 1, men i det här fallet är den enda genomförbara policyn att välja den första sökanden, och därmed P (1) = 1/ n . Denna summa erhålls genom att notera att om sökande i är den bästa sökanden så väljs den ut om och endast om den bästa sökanden bland de första i − 1 sökandena är bland de första r − 1 sökandena som avslogs. Genom att låta n tendera till oändligheten, skriva $x$ som gränsen för (r−1) / n , med t för (i−1) / n och dt för 1/ n , summan kan approximeras med integralen

$P(x)=x\int _{x}^{1}{\frac {1}{t}}\,dt=-x\ln(x)\;.$

Om vi ​​tar derivatan av P ( x ) med avseende på ${\displaystyle x} ,$ sätter den till 0 och löser för x , finner vi att det optimala x är lika med 1/ e . Således tenderar den optimala cutoff att n / e när n ökar och den bästa sökanden väljs med sannolikhet 1 / e .

För små värden på n kan det optimala r också erhållas med dynamiska standardprogrammeringsmetoder. De optimala tröskelvärdena r och sannolikheten för att välja det bästa alternativet P för flera värden på n visas i följande tabell.

$n$	1	2	3	4	5	6	7	8	9
$r$	1	1	2	2	3	3	3	4	4
$P$	1 000	0,500	0,500	0,458	0,433	0,428	0,414	0,410	0,406

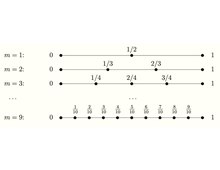
Sannolikheten att välja den bästa sökanden i det klassiska sekreterarproblemet konvergerar mot $1/e\approx 0,368$ .

Alternativ lösning

Detta problem och flera modifieringar kan lösas (inklusive beviset på optimalitet) på ett enkelt sätt med oddsalgoritmen , som också har andra tillämpningar. Modifieringar för sekreterarproblemet som kan lösas med denna algoritm inkluderar slumpmässiga tillgänglighet av sökande, mer generella hypoteser för att sökande ska vara av intresse för beslutsfattare, gruppintervjuer för sökande, samt vissa modeller för ett slumpmässigt antal sökande.

Begränsningar

Lösningen av sekreterarproblemet är bara meningsfullt om det är motiverat att anta att de sökande inte har någon kännedom om vilken beslutsstrategi som används, eftersom tidiga sökande inte har någon chans alls och kanske inte dyker upp annars.

En viktig nackdel för tillämpningar av lösningen av det klassiska sekreterarproblemet är att antalet sökande $n$ måste vara känt i förväg, vilket sällan är fallet. Ett sätt att övervinna detta problem är att anta att antalet sökande är en slumpvariabel $N$ med en känd fördelning av $P(N=k )_{k=1,2,\cdots }$ (Presman och Sonin, 1972). För denna modell är dock den optimala lösningen i allmänhet mycket svårare. Dessutom är den optimala framgångssannolikheten nu inte längre runt 1/ e utan vanligtvis lägre. Detta kan förstås i sammanhanget att man har ett "pris" att betala för att man inte känner till antalet sökande. Men i denna modell är priset högt. Beroende på valet av fördelningen av $N$ kan den optimala vinstsannolikheten närma sig noll. Att leta efter sätt att hantera detta nya problem ledde till en ny modell som gav den så kallade 1/e-lagen av bästa val.

1/e-lag av bästa val

Kärnan i modellen är baserad på idén att livet är sekventiellt och att verkliga problem uppstår i realtid. Det är också lättare att uppskatta tidpunkter då specifika händelser (ankomst av sökande) bör inträffa oftare (om de gör det) än att uppskatta fördelningen av antalet specifika händelser som kommer att inträffa. Denna idé ledde till följande tillvägagångssätt, det så kallade enhetliga tillvägagångssättet (1984):

Modellen definieras enligt följande: En sökande måste väljas på ett visst tidsintervall $[0,T]$ från ett okänt antal $N$ av rankbara sökande. Målet är att maximera sannolikheten att endast välja det bästa under hypotesen att alla ankomstordrar av olika rang är lika sannolika. Antag att alla sökande har samma, men oberoende av varandra, ankomsttid $f$ på $[0,T]$ och låt $F$ beteckna motsvarande ankomsttid distributionsfunktion, det vill säga

$F(t)=\int _{0}^{t}f(s)ds$ , $\,0\leq t\leq T$ .

Låt $\tau$ vara sådan att $F(\tau )=1/e.$ Överväg strategin att vänta och observera alla sökande fram till tiden $\tau$ och sedan välja, om möjligt, den första kandidaten efter tiden $\tau$ vilket är bättre än alla föregående. Då har den här strategin, kallad 1/e-strategy , följande egenskaper:

1 /e-strategin

(i) ger för alla $N$ en framgångssannolikhet på minst 1/e,

(ii) är en minimax-optimal strategi för väljaren som inte känner till ${\displaystyle N} ,$ (

iii) väljer, om det finns minst en sökande, ingen alls med sannolikhet exakt 1/e.

1/e-lagen, bevisad 1984 av F. Thomas Bruss , kom som en överraskning. Anledningen var att ett värde på cirka 1/e tidigare hade ansetts vara utom räckhåll i en modell för okänd $N$ , medan detta värde 1/e nu uppnåddes som en nedre gräns för framgångssannolikheten, och detta i en modell med förmodligen mycket svagare hypoteser (se t.ex. Math. Recensioner 85:m).

Det finns dock många andra strategier som uppnår (i) och (ii) och dessutom presterar strikt bättre än 1/e-strategin samtidigt för alla N {\displaystyle N} $2$ . Ett enkelt exempel är strategin som väljer ut (om möjligt) den första relativt bästa kandidaten efter tid $\tau$ förutsatt att minst en sökande anlände före denna tidpunkt, och annars väljer (om möjligt) den näst relativt bästa kandidaten efter tid $\tau$ .

1/e-lagen förväxlas ibland med lösningen på det klassiska sekreterarproblemet som beskrivs ovan på grund av den liknande rollen för numret 1/e. I 1/e-lagen är dock denna roll mer generell. Resultatet är också starkare, eftersom det gäller för ett okänt antal sökande och eftersom modellen baserad på en ankomsttidsfördelning F är mer lättillgänglig för ansökningar.

Spelet Google

Enligt Thomas S. Ferguson dök sekreterarproblemet upp för första gången i tryck när det presenterades av Martin Gardner i hans Mathematical Games-kolumn i februari 1960 i Scientific American . Så här formulerade Gardner det: "Be någon att ta så många papperslappar han vill och skriv ett annat positivt tal på varje lapp. Siffrorna kan variera från små bråkdelar av 1 till ett tal som är lika stort som en googol ( 1 ) följt av hundra nollor) eller ännu större. Dessa lappar vänds med framsidan nedåt och blandas över toppen av ett bord. En i taget vänder du lapparna med framsidan uppåt. Målet är att sluta vända när du kommer till siffran som du gissar på att vara den största i serien. Du kan inte gå tillbaka och välja en tidigare vänd lapp. Om du vänder på alla lappar måste du naturligtvis välja den senast vända lappen."

I artikeln "Vem löste sekreterarproblemet?" Ferguson påpekade att sekreterarproblemet förblev olöst som det påstods av M. Gardner, det vill säga som ett tvåpersoners nollsummespel med två antagonistiska spelare. I det här spelet skriver Alice, den informerade spelaren, i hemlighet distinkta nummer på $n$ kort. Bob, den stoppande spelaren, observerar de faktiska värdena och kan sluta vända kort när han vill, vinna om det senast vände kortet har det totala maximala antalet. Skillnaden med det grundläggande sekreterarproblemet är att Bob observerar de faktiska värdena som är skrivna på korten, som han kan använda i sina beslutsprocedurer. Siffrorna på korten är analoga med de numeriska egenskaperna hos sökande i vissa versioner av sekreterarproblemet. Den gemensamma sannolikhetsfördelningen av siffrorna är under kontroll av Alice.

Bob vill gissa det maximala antalet med högsta möjliga sannolikhet, medan Alices mål är att hålla denna sannolikhet så låg som möjligt. Det är inte optimalt för Alice att ta prov på siffrorna oberoende av någon fast fördelning, och hon kan spela bättre genom att välja slumpmässiga nummer på något beroende sätt. För $n=2$ har Alice ingen minimaxstrategi , vilket är nära relaterat till en paradox med T. Cover . Men för $n>2$ har spelet en lösning: Alice kan välja slumptal (som är beroende slumpvariabler) på ett sådant sätt att Bob inte kan spela bättre än att använda den klassiska stoppstrategin baserad på de relativa rangorden .

Heuristisk prestanda

Resten av artikeln behandlar återigen sekreterarproblemet för ett känt antal sökande.

Förväntade framgångssannolikheter för tre heuristiker.

Stein, Seale & Rapoport 2003 härledde de förväntade framgångssannolikheterna för flera psykologiskt rimliga heuristiker som kan användas i sekreterarproblemet. Heuristiken de undersökte var:

• Cutoff-regeln (CR): Acceptera inte någon av de första y sökandena; välj därefter den första som stött på kandidaten (dvs. en sökande med relativ rang 1). Denna regel har som ett specialfall den optimala policyn för det klassiska sekreterarproblemet för vilket y = r .
• Kandidaträkningsregel (CCR): Välj den y -th påträffade kandidaten. Observera att denna regel inte nödvändigtvis hoppar över några sökande; den tar bara hänsyn till hur många kandidater som har observerats, inte hur djupt beslutsfattaren är i sökandesekvensen.
• Successiv icke-kandidatregel (SNCR): Välj den första som stöter på kandidaten efter att ha observerat y icke-kandidater (dvs sökande med relativ rang > 1).

Varje heuristik har en enda parameter y . Figuren (visad till höger) visar de förväntade framgångssannolikheterna för varje heuristik som funktion av y för problem med n = 80.

Cardinal payoff variant

Att hitta den enskilt bästa sökanden kan tyckas vara ett ganska strikt mål. Man kan tänka sig att intervjuaren hellre anställer en högre värderad sökande än en lägre värderad, och inte bara sysslar med att få det bästa. Det vill säga, intervjuaren kommer att få ett visst värde från att välja en sökande som inte nödvändigtvis är den bästa, och det härledda värdet ökar med värdet av den som väljs ut.

För att modellera detta problem, anta att de $n$ sökandena har "sanna" värden som är slumpvariabler X dras iid från en enhetlig fördelning på [0, 1]. I likhet med det klassiska problemet som beskrivs ovan, observerar intervjuaren bara om varje sökande är bäst hittills (en kandidat), måste acceptera eller avvisa var och en på plats och måste acceptera den sista om han/hon nås. (För att vara tydlig, intervjuaren lär sig inte den faktiska relativa rangordningen för varje sökande. Han/hon lär sig bara om den sökande har relativ rang 1.) Men i denna version ges utdelningen av det verkliga värdet av den valda sökanden. Till exempel, om han/hon väljer en sökande vars verkliga värde är 0,8, kommer han/hon att tjäna 0,8. Intervjuarens mål är att maximera det förväntade värdet för den valda sökanden.

Eftersom sökandens värden är iid hämtas från en enhetlig fördelning på [0, 1], det förväntade värdet för den t :e sökanden givet att $x_{t }=\max \left\{x_{1},x_{2},\ldots ,x_{t}\right\}$ ges av

$E_{t}=E\left(X_{t}|I_{t}=1\right)={\frac {t}{t+1}}.$

Liksom i det klassiska problemet ges den optimala policyn av en tröskel, som vi för detta problem kommer att beteckna med ${\displaystyle c} ,$ vid vilken intervjuaren ska börja acceptera kandidater. Bearden visade att c är antingen $\lfloor {\sqrt {n}}\rfloor$ eller $\lceil {\sqrt {n}}\rceil$ . (Faktum är att det som är närmast ${\displaystyle {\sqrt {n}}} .$ ) Detta följer av det faktum att givet ett problem med $n$ sökande, är den förväntade utdelningen för en godtycklig tröskel $1\leq c\leq n$ är

$V_{n}(c)=\sum _{t=c}^{n-1}\left[\prod _{s=c}^{t-1}\left({\frac {s -1}{s}}\right)\right]\left({\frac {1}{t+1}}\right)+\left[\prod _{s=c}^{n-1}\ vänster({\frac {s-1}{s}}\right)\right]{\frac {1}{2}}={\frac {2cn-{c}^{2}+cn}{2cn} }.$

Att differentiera $V_{n}(c)$ med avseende på c , får man

${\frac {\partial V}{\partial c}}={\frac {-{c}^{\,2}+n}{2{c}^{\,2}n}}.$

Lärande i det sekventiella sökparadigmet med partiell information. Siffrorna visar förväntade värden för sökande baserat på deras relativa rang (av m totalt sett hittills sökande) vid olika punkter i sökningen. Förväntningarna beräknas baserat på fallet när deras värden är jämnt fördelade mellan 0 och 1. Relativ ranginformation gör det möjligt för intervjuaren att bättre utvärdera sökande eftersom de samlar på sig fler datapunkter att jämföra dem med.

Eftersom $\partial ^{\,2}V/\partial c^{\,2}<0$ för alla tillåtna värden på $c$ finner vi att $V$ är maximerad till $c={\sqrt {n}}$ . Eftersom V är konvex i $c$ måste den optimala heltalsvärdeströskeln vara antingen $\lfloor {\sqrt {n}}\rfloor$ eller $\lceil {\ sqrt {n}}\rceil$ . För de flesta värden på $n$ kommer således intervjuaren att börja acceptera sökande snabbare i kardinalutbetalningsversionen än i den klassiska versionen där målet är att välja den enskilt bästa sökanden. Observera att detta inte är ett asymptotiskt resultat: Det gäller för alla $n$ . Detta är dock inte den optimala policyn för att maximera förväntat värde från en känd fördelning. Vid en känd fördelning kan optimalt spel beräknas via dynamisk programmering.

En mer generell form av detta problem introducerad av Palley och Kremer (2014) antar att när varje ny sökande kommer, observerar intervjuaren deras rangordning i förhållande till alla sökande som har observerats tidigare. Denna modell överensstämmer med föreställningen om att en intervjuare lär sig när de fortsätter sökprocessen genom att samla en uppsättning tidigare datapunkter som de kan använda för att utvärdera nya kandidater när de anländer. En fördel med denna så kallade partiell informationsmodell är att beslut och uppnådda resultat givet den relativa ranginformationen kan jämföras direkt med motsvarande optimala beslut och utfall om intervjuaren hade fått fullständig information om värdet av varje sökande. Detta problem med fullständig information, där sökande dras oberoende av en känd fördelning och intervjuaren försöker maximera det förväntade värdet av den sökande som valts ut, löstes ursprungligen av Moser (1956), Sakaguchi (1961) och Karlin (1962).

Andra modifieringar

Det finns flera varianter av sekreterarproblemet som också har enkla och eleganta lösningar.

En variant ersätter viljan att välja det bästa med önskan att välja den näst bästa. Robert J. Vanderbei kallar detta "postdoc"-problemet och hävdar att de "bästa" kommer att gå till Harvard. För detta problem är sannolikheten för framgång för ett jämnt antal sökande exakt ${\frac {0,25n^{2}}{n(n-1)}}$ . Denna sannolikhet tenderar till 1/4 eftersom n tenderar till oändlighet, vilket illustrerar det faktum att det är lättare att välja det bästa än det näst bästa.

För en andra variant är antalet val specificerat till att vara större än ett. Med andra ord, intervjuaren anställer inte bara en sekreterare utan släpper till exempel in en klass av studenter från en sökandepool. Under antagandet att framgång uppnås om och endast om alla utvalda kandidater är överlägsna alla de icke utvalda kandidaterna, är det återigen ett problem som kan lösas. Det visades i Vanderbei 1980 att när n är jämnt och önskan är att välja exakt hälften av kandidaterna, ger den optimala strategin en framgångssannolikhet på ${\frac {1}{n/2+ 1}}$ .

En annan variant är att välja de bästa $k$ -sekreterarna ur en pool av ${\displaystyle n} ,$ återigen i en onlinealgoritm. Detta leder till en strategi relaterad till den klassiska ettan och cutoff-tröskeln på ${\frac {0.25n^{2}}{n(n-1)}}$ för vilken klassiska problem är ett specialfall.

Flervalsproblem

En spelare tillåts $r$ val, och han vinner om något val är det bästa. Gilbert & Mosteller 1966 visade att en optimal strategi ges av en tröskelstrategi (cutoff-strategi). En optimal strategi tillhör den klass av strategier som definieras av en uppsättning tröskelvärden $(a_{1},a_{2},...,a_{ r})$ , där $a_{1}<a_{2}<\cdots <a_{r}$ . Det första valet ska användas på de första kandidaterna som börjar med ${\displaystyle a_{1}}:$ e sökande, och när det första valet har använts ska andra valet användas på den första kandidaten som börjar med ${\ displaystyle a_{2}}$ :e sökande, och så vidare.

$Gilbert$ och Mosteller visade att $displaystyle \left({\frac {a_{1}}{n}},{\frac {a_{2}}{n}},{\frac {a_{3}}{n}},{\frac { a_{4}}{n}}\right)\rightarrow \left(e^{-1},e^{-{\frac {3}{2}}},e^{-{\frac {47} {24}}},e^{-{\frac {2761}{1152}}}\right)(n\högerpil \infty )}$ . För ytterligare fall att $r=5,6,...,10$ , se Matsui & Ano 2016 (till exempel ${\displaystyle {\frac {a_{5}}{n}} \rightarrow e^{-{\frac {4162637}{1474560}}}})$ .

När $r=2$ konvergerar sannolikheten för vinst till $e^{-1}+e^{-{\frac {3 }{2}}}(n\högerpil \infty )$ . Matsui & Ano 2016 visade att för varje positivt heltal ${\displaystyle r} konvergerar$ sannolikheten för vinst (för $r$ valsekreterareproblem) till $p_{ 1}+p_{2}+\cdots +p_{r}$ där $p_{i}=\lim _{n\rightarrow \infty }{\frac {a_ {i}}{n}}$ . Således konvergerar sannolikheten för vinst till $e^{-1}+e^{-{\frac {3}{2}}}+e^{ -{\frac {47}{24}}}$ och $e^{-1}+e^{-{\frac { 3}{2}}}+e^{-{\frac {47}{24}}}+e^{-{\frac {2761}{1152}}}$ när $r =3,4$ respektive.

Experimentella studier

Experimentella psykologer och ekonomer har studerat beslutsbeteendet hos faktiska personer i sekreterarproblem. Till stor del har detta arbete visat att människor tenderar att sluta söka för tidigt. Detta kan åtminstone delvis förklaras av kostnaden för att utvärdera kandidater. I verkliga miljöer kan detta tyda på att människor inte söker tillräckligt när de ställs inför problem där beslutsalternativen stöter på sekventiellt. Till exempel, när man försöker bestämma sig vid vilken bensinstation längs en motorväg man ska stanna för bensin, kanske folk inte letar tillräckligt innan de stannar. Om det var sant, skulle de tendera att betala mer för gas än om de hade letat längre. Detsamma kan vara sant när människor söker på nätet efter flygbiljetter. Experimentell forskning om problem som sekreterarproblemet kallas ibland beteendeoperationsforskning .

Neural korrelerar

Även om det finns en betydande mängd neurovetenskaplig forskning om informationsintegration, eller representation av tro, i perceptuella beslutsfattande uppgifter med användning av både djur och människor, är det relativt lite känt om hur beslutet att sluta samla information kommer fram.

Forskare har studerat de neurala grunderna för att lösa sekreterarproblemet hos friska frivilliga med hjälp av funktionell MRT . En Markov-beslutsprocess (MDP) användes för att kvantifiera värdet av att fortsätta söka kontra att förbinda sig till det aktuella alternativet. Beslut att ta kontra avslå ett alternativ engagerade parietala och dorsolaterala prefrontala cortex, samt ventral striatum , anterior insula och anterior cingulate . Därför kodar hjärnregioner som tidigare var inblandade i bevisintegrering och belöningsrepresentation tröskelövergångar som utlöser beslut att förbinda sig till ett val.

Historia

Sekreterarproblemet introducerades tydligen 1949 av Merrill M. Flood , som kallade det fästmöproblemet i en föreläsning han höll samma år. Han hänvisade till det flera gånger under 1950-talet, till exempel i ett konferenstal i Purdue den 9 maj 1958, och det blev så småningom allmänt känt i folkloren även om ingenting publicerades vid den tiden. År 1958 skickade han ett brev till Leonard Gillman , med kopior till ett dussin vänner inklusive Samuel Karlin och J. Robbins, där han beskrev ett bevis på den optimala strategin, med en bilaga av R. Palermo som bevisade att alla strategier domineras av en strategi av formen "förkasta första p villkorslöst, acceptera sedan nästa kandidat som är bättre".

Den första publikationen var tydligen av Martin Gardner i Scientific American, februari 1960. Han hade hört talas om det från John H. Fox Jr. och L. Gerald Marnie, som självständigt hade kommit på ett motsvarande problem 1958; de kallade det "game of googol". Fox och Marnie visste inte den optimala lösningen; Gardner bad om råd från Leo Moser , som (tillsammans med JR Pounder) gav en korrekt analys för publicering i tidningen. Strax efteråt skrev flera matematiker till Gardner för att berätta om motsvarande problem som de hade hört via vinrankan, som alla med största sannolikhet kan spåras till Floods ursprungliga verk.

1/ e -lagen av bästa val beror på F. Thomas Bruss .

Ferguson har en omfattande bibliografi och påpekar att ett liknande (men annorlunda) problem hade övervägts av Arthur Cayley 1875 och även av Johannes Kepler långt dessförinnan.

Kombinatorisk generalisering

Sekreterarproblemet kan generaliseras till det fall där det finns flera olika jobb. Återigen, det finns $n$ sökande som kommer i slumpmässig ordning. När en kandidat anländer avslöjar hon en uppsättning icke-negativa siffror. Varje värde anger hennes kvalifikationer för ett av jobben. Handläggaren måste inte bara besluta om den sökande ska anställas eller inte utan måste i så fall även anställa henne permanent till ett av jobben. Målet är att hitta ett uppdrag där summan av meriter är så stor som möjligt. Detta problem är identiskt med att hitta en maximalviktsmatchning i en kantviktad tvådelad graf där de $n$ -noderna på en sida kommer online i slumpmässig ordning. Det är alltså ett specialfall av online-bipartsmatchningsproblemet .

Genom en generalisering av den klassiska algoritmen för sekreterarproblemet är det möjligt att få ett uppdrag där den förväntade summan av kvalifikationer endast är en faktor e {\ $e}$ mindre än en optimal (offline) tilldelning.

Se även

• Uppdragsproblem
• Oddsalgoritm
• Optimalt stopp
• Robbins problem
• Sökteori
• Stabilt äktenskapsproblem

Anteckningar

• Bearden, JN (2006). "Ett nytt sekreterareproblem med rangbaserat urval och kardinalutbetalningar". Journal of Mathematical Psychology . 50 : 58–9. doi : 10.1016/j.jmp.2005.11.003 .
•    Bearden, JN; Murphy, RO; Rapoport, A. (2005). "En förlängning av flera attribut av sekreterarproblemet: teori och experiment". Journal of Mathematical Psychology . 49 (5): 410–425. CiteSeerX 10.1.1.497.6468 . doi : 10.1016/j.jmp.2005.08.002 . S2CID 9186039 .
• Bearden, J. Neil; Rapoport, Amnon; Murphy, Ryan O. (september 2006). "Sekventiell observation och urval med rangberoende utbetalningar: en experimentell studie". Management Science . 52 (9): 1437–1449. doi : 10.1287/mnsc.1060.0535 .
• Bruss, F. Thomas (juni 2000). "Summera oddsen till ett och sluta" . Sannolikhetens annaler . 28 (3): 1384–1391. doi : 10.1214/aop/1019160340 .
• Bruss, F. Thomas (oktober 2003). "En notering om gränser för oddssatsen om optimalt stopp" . Sannolikhetens annaler . 31 (4): 1859–1961. doi : 10.1214/aop/1068646368 .
• Bruss, F. Thomas (augusti 1984). "En enhetlig strategi för en klass av bästa valproblem med ett okänt antal alternativ" . Sannolikhetens annaler . 12 (3): 882–889. doi : 10.1214/aop/1176993237 .
• Flood, Merrill R. (1958). "Bevis på den optimala strategin". Brev till Martin Gardner. Martin Gardner papper serie 1, ruta 5, mapp 19: Stanford University Archives. {{ citera pressmeddelande }} : CS1 underhåll: plats ( länk )
•   Freeman, PR (1983). "Sekreterarproblemet och dess förlängningar: En recension". International Statistical Review / Revue Internationale de Statistique . 51 (2): 189–206. doi : 10.2307/1402748 . JSTOR 1402748 .
• Gardner, Martin (1966). "3". Nya matematiska avledningar från Scientific American . Simon och Schuster. [skriver om sin ursprungliga kolumn publicerad i februari 1960 med ytterligare kommentarer]
•     Girdhar, Yogesh; Dudek, Gregory (2009). "Optimal onlinedatasampling eller hur man anställer de bästa sekreterarna". 2009 kanadensisk konferens om dator- och robotseende . s. 292–298. CiteSeerX 10.1.1.161.41 . doi : 10.1109/CRV.2009.30 . ISBN 978-1-4244-4211-9 . S2CID 2742443 .
•   Gilbert, J; Mosteller, F (1966). "Kenkänna det maximala av en sekvens". Journal of the American Statistical Association . 61 (313): 35–73. doi : 10.2307/2283044 . JSTOR 2283044 .
• Gnedin, A. (1994). "En lösning på spelet Googol" . Annals of Probability . 22 (3): 1588–1595. doi : 10.1214/aop/1176988613 .
•   Gnedin, A. (2021). "Det bästa valproblemet med slumpmässiga ankomster: Hur man slår 1/e-strategin". Stokastiska processer och deras tillämpningar . 145 : 226–240. doi : 10.1016/j.spa.2021.12.008 . S2CID 245449000 .
• Hill, TP " Att veta när man ska sluta ". American Scientist , vol. 97, 126-133 (2009). (För fransk översättning, se omslagsartikel i julinumret av Pour la Science (2009))
•   Ketelaar, Timothy; Todd, Peter M. (2001). "Ramar in våra tankar: ekologisk rationalitet som evolutionär psykologins svar på ramproblemet". Konceptuella utmaningar i evolutionär psykologi . Studier i kognitiva system. Vol. 27. s. 179–211. doi : 10.1007/978-94-010-0618-7_7 . ISBN 978-94-010-3890-4 .
•   Matsui, T; Ano, K (2016). "Lägre gränser för Bruss oddsproblem med flera stopp". Operationsforskningens matematik . 41 (2): 700–714. arXiv : 1204.5537 . doi : 10.1287/moor.2015.0748 . S2CID 31778896 .
•   Miller, Geoffrey F. (2001). Parningssinnet: hur sexuella val formade utvecklingen av den mänskliga naturen . Ankare böcker. ISBN 978-0-385-49517-2 .
•   Sardelis, Dimitris A.; Valahas, Theodoros M. (mars 1999). "Beslutsfattande: En gyllene regel". American Mathematical Monthly . 106 (3): 215. doi : 10.2307/2589677 . JSTOR 2589677 .
• Seale, DA; Rapoport, A. (1997). "Sekventiellt beslutsfattande med relativa led: En experimentell undersökning av "sekreterareproblemet" " . Organisationsbeteende och mänskliga beslutsprocesser . 69 (3): 221–236. doi : 10.1006/obhd.1997.2683 .
• Stein, WE; Seale, DA; Rapoport, A. (2003). "Analys av heuristiska lösningar på problemet med bästa val". European Journal of Operational Research . 151 : 140–152. doi : 10.1016/S0377-2217(02)00601-X .
• Vanderbei, RJ (november 1980). "Det optimala valet av en delmängd av en befolkning". Operationsforskningens matematik . 5 (4): 481–486. doi : 10.1287/moor.5.4.481 .
•   Vanderbei, Robert J. (2012). "Postdokvarianten av sekreterarproblemet" (PDF) . CiteSeerX 10.1.1.366.1718 . {{ citera journal }} : Citera journal kräver |journal= ( hjälp )

externa länkar

• OEIS -sekvens A054404 (Antal döttrar att vänta innan de plockar in sultanens hemgiftsproblem med n döttrar)
• Weisstein, Eric W. "Sultans hemgiftsproblem" . MathWorld .
• Neil Bearden. "Optimal sökning (sekreterareproblem)" . Arkiverad från originalet den 4 januari 2017.
• Optimal Stopping and Applications av Thomas S. Ferguson