Roche lob

Detta är en schematisk bild av ett parhus binärt system där den större komponenten fyller dess Roche-lob (svart linje).

Inom astronomi är Roche -loben regionen runt en stjärna i ett binärt system inom vilket kretsande material är gravitationsbundet till den stjärnan. Det är en ungefärlig droppformad region som begränsas av en kritisk gravitationsekvipotential , med spetsen av tårdroppen pekar mot den andra stjärnan (spetsen är på L 1 _Lagrangian pekar av systemet).

Roche-loben skiljer sig från Roche-sfären , som närmar sig gravitationssfären av påverkan av en astronomisk kropp inför störningar från en mer massiv kropp som den kretsar runt. Det skiljer sig också från Roche-gränsen , som är det avstånd på vilket ett föremål som hålls samman endast av gravitationen börjar brytas upp på grund av tidvattenkrafter . Roche-loben, Roche-gränsen och Roche-sfären är uppkallade efter den franske astronomen Édouard Roche .

Definition

En tredimensionell representation av Roche-potentialen i en dubbelstjärna med ett massförhållande på 2, i den samroterande ramen. De droppformade figurerna i ekvipotentialdiagrammet längst ner i figuren definierar vad som anses vara stjärnornas Rochelober. L ₁ , L ₂ och L ₃ är de lagrangiska punkter där krafter (betraktade i den roterande ramen) tar ut. Massa kan flöda genom sadelpunkten L ₁ från en stjärna till dess följeslagare, om stjärnan fyller sin Roche-lob.

STL 3D-modell av Roche-potentialen hos två kretsande kroppar, renderad till hälften som en yta och hälften som ett nät

I ett binärt system med en cirkulär bana är det ofta användbart att beskriva systemet i ett koordinatsystem som roterar tillsammans med objekten. I denna icke-tröghetsram måste man ta hänsyn till centrifugalkraften utöver gravitationen. De två tillsammans kan beskrivas med en potential , så att till exempel stjärnytorna ligger längs ekvipotentiella ytor.

Nära varje stjärna är ytor med samma gravitationspotential ungefär sfäriska och koncentriska med den närmaste stjärnan. Långt från stjärnsystemet är ekvipotentialerna ungefär ellipsoida och långsträckta parallellt med axeln som förenar stjärncentrumen. En kritisk ekvipotential skär sig vid L ₁ Lagrangian-punkten i systemet och bildar en tvålobig åttafigur med en av de två stjärnorna i mitten av varje lob. Denna kritiska ekvipotential definierar Roche-loberna.

Där materia rör sig i förhållande till den samroterande ramen kommer den att tyckas påverkas av en Corioliskraft . Detta kan inte härledas från Roche-lobmodellen eftersom Corioliskraften är en icke- konservativ kraft (dvs. inte kan representeras av en skalär potential).

Vidare analys

Potentiell array

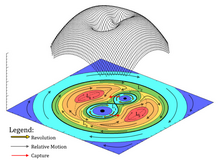
I gravitationspotentialgrafiken är L ₁ , L ₂ , L ₃ , L ₄ , L ₅ i synkron rotation med systemet. Regioner av rött, orange, gult, grönt, ljusblått och blått är potentiella arrayer från hög till låg. Röda pilar är rotation av systemet och svarta pilar är relativa rörelser av skräpet.

Skräp går snabbare i regionen med lägre potential och långsammare i regionen med högre potential. Så, relativa rörelser av skräpet i den nedre omloppsbanan är i samma riktning som systemets rotation medan motsatta i den högre omloppsbanan.

L ₁ är gravitationsfångningsjämviktspunkten. Det är en gravitationsgräns för det binära stjärnsystemet. Det är den minsta potentiella jämvikten mellan L ₁ , L ₂ , L ₃ , L ₄ och L ₅ . Det är det enklaste sättet för skräpet att pendla mellan en Hill-sfär (en inre cirkel av blått och ljusblått) och kommunala gravitationsregioner (åttor i gult och grönt på insidan).

Hillsfär och hästskobana

L ₂ och L ₃ är gravitationella störningsjämviktspunkter. Genom att passera genom dessa två jämviktspunkter kan skräp pendla mellan det yttre området (åtta i gult och grönt på utsidan) och det binära systemets kommunala gravitationsregion.

L ₄ och L ₅ är de maximala potentiella punkterna i systemet. De är instabila jämvikter. Om massförhållandet mellan de två stjärnorna blir större, kommer de orange, gula och gröna områdena att bli en hästskobana .

Det röda området kommer att bli grodyngelbanan .

Massöverföring

När en stjärna "överstiger sin Roche-lob" sträcker sig dess yta ut utanför dess Roche-lob och materialet som ligger utanför Roche-loben kan "falla av" in i det andra objektets Roche-lob via den första Lagrangian-punkten. I binär evolution kallas detta massöverföring via Roche-lobe overflow .

I princip kan massöverföring leda till total sönderfall av föremålet, eftersom en minskning av föremålets massa får dess Roche-lob att krympa. Det finns dock flera anledningar till att detta inte sker generellt. För det första kan en minskning av givarstjärnans massa göra att givarstjärnan också krymper, vilket möjligen förhindrar ett sådant resultat. För det andra, med överföringen av massa mellan de två binära komponenterna, överförs också vinkelmomentum . Medan massöverföring från en mer massiv donator till en mindre massiv ackretor i allmänhet leder till en krympande omloppsbana, orsakar det omvända omloppsbanan att expandera (under antagandet om bevarande av massa och vinkelmoment). Expansionen av den binära omloppsbanan kommer att leda till en mindre dramatisk krympning eller till och med expansion av donatorns Roche-lob, vilket ofta förhindrar att donatorn förstörs.

För att bestämma stabiliteten hos massöverföringen och därmed givarstjärnans exakta öde, måste man ta hänsyn till hur donatorstjärnans radie och dess Roche-lob reagerar på massförlusten från donatorn; om stjärnan expanderar snabbare än dess Roche-lob eller krymper mindre snabbt än dess Roche-lob under en längre tid, kommer massöverföringen att bli instabil och donatorstjärnan kan sönderfalla. Om donatorstjärnan expanderar mindre snabbt eller krymper snabbare än dess Roche-lob kommer massöverföringen i allmänhet att vara stabil och kan fortsätta under lång tid.

Massöverföring på grund av översvämning av Roche-loben är ansvarig för ett antal astronomiska fenomen, inklusive Algol-system , återkommande novaer ( dubbelstjärnor som består av en röd jätte och en vit dvärg som är tillräckligt nära att material från den röda jätten dribbla ner på den vita dvärg), röntgenbinärer och millisekundspulsarer . Sådan massöverföring av Roche lobe overflow (RLOF) är ytterligare uppdelad i tre distinkta fall:

Fall A

Fall A RLOF uppstår när donatorstjärnan brinner väte . Enligt Nelson och Eggleton finns det ett antal underklasser som återges här:

AD dynamisk

när RLOF råkar ut för en stjärna med en djup konvektionszon . Massöverföring sker snabbt på stjärnans dynamiska tidsskala och kan sluta med en fullständig sammanslagning .

AR snabb kontakt

liknar AD, men när stjärnan som materia snabbt ansamlas på får massa, får den tillräckligt med fysisk storlek för att den ska nå sin egen Roche-lob. Som sådana gånger manifesterar systemet sig som en kontaktbinär, såsom en W Ursae Majoris-variabel .

SOM långsam kontakt

liknar AR, men bara en kort period av snabb massöverföring sker följt av en mycket längre period av långsam massöverföring. Så småningom kommer stjärnorna att komma i kontakt, men de har förändrats avsevärt när detta händer. Algolvariabler är resultatet av sådana situationer.

AE tidig omkörning

liknar AS, men stjärnan som får massa går om stjärnan som donerar massa för att utvecklas förbi huvudsekvensen. Givarstjärnan kan krympa så lite för att stoppa massöverföring, men så småningom kommer massöverföringen att börja igen när stjärnutvecklingen fortsätter att leda till fallen

AL sen omkörning

fallet när stjärnan som ursprungligen var givaren genomgår en supernova efter att den andra stjärnan har genomgått en egen omgång av RLOF.

AB binär

fallet där stjärnorna växlar fram och tillbaka mellan vilka en genomgår RLOF minst tre gånger (tekniskt sett en underklass av ovanstående).

AN ingen omkörning

fallet när stjärnan som ursprungligen var donatorn genomgår en supernova innan den andra stjärnan når en RLOF-fas.

AG jätte

Massöverföringen börjar inte förrän stjärnan når den röda jättegrenen utan innan den har tömt sin vätekärna (varefter systemet beskrivs som fall B).

Fall B

Fall B inträffar när RLOF startar medan givaren är en stjärna som brinner efter kärnan av väte/väteskal. Detta fall kan ytterligare delas in i klasserna Br och Bc beroende på om massöverföringen sker från en stjärna som domineras av en strålningszon (Br) och därför utvecklas som situationen med de flesta fall A RLOF eller en konvektiv zon (Bc) varefter en vanlig kuvertfas kan förekomma (liknande fall C). En alternativ uppdelning av fall är Ba, Bb och Bc som ungefär motsvarar RLOF-faser som sker under heliumfusion, efter heliumfusion men före kolfusion, eller efter kolfusion i den högt utvecklade stjärnan.

Fall C

Fall C inträffar när RLOF startar när donatorn är vid eller bortom heliumskalets bränningsfas. Dessa system är de mest sällsynta som observerats, men detta kan bero på urvalsbias .

Geometri

Den exakta formen på Roche-loben beror på massförhållandet $q=M_{1}/M_{2}$ och måste utvärderas numeriskt. För många ändamål är det emellertid användbart att approximera Roche-loben som en sfär med samma volym. En ungefärlig formel för radien för denna sfär är

{\displaystyle {\frac {r_{1}}{A}}=\max {[f_{1},f_{2}]}} ,

för

0<q<20

där $f_{1}=0,38+0,2\log {q}$ $displaystyle f_{2}=0,46224 \left({\frac {q}{1+q}}\right)^{1/3}}$ 2 . Funktion $f_{1}$ är större än $f_{2}$ för $q\gtrsim 0,5228$ . Längden A är den orbitala separationen av systemet och r ₁ är radien för den sfär vars volym närmar sig Roche-loben med massan M ₁ . Denna formel är korrekt till inom cirka 2%. En annan ungefärlig formel föreslogs av Eggleton och lyder som följer: