Randvillkor i vätskedynamik

Randvillkor i vätskedynamik är uppsättningen av begränsningar för problem med gränsvärden i beräkningsvätskedynamik . Dessa gränsvillkor inkluderar inloppsgränsvillkor, utloppsgränsvillkor, vägggränsvillkor, konstanttrycksgränsvillkor, axisymmetriska gränsvillkor, symmetriska gränsvillkor och periodiska eller cykliska gränsvillkor.

Övergående problem kräver ytterligare en sak, dvs initiala förhållanden där initiala värden för flödesvariabler specificeras vid noder i flödesdomänen. Olika typer av randvillkor används i CFD för olika förhållanden och syften och diskuteras enligt följande.

Inloppsgränsförhållanden

Visar inloppsflödeshastighet i ett rör

I inloppsgränsförhållanden måste fördelningen av alla flödesvariabler specificeras vid inloppsgränser, huvudsakligen flödeshastighet . Denna typ av randvillkor är vanliga och specificeras mest där inloppsflödeshastigheten är känd.

Utlopps gränsvillkor

Visar utloppsflödeshastighet i ett rör

I utloppsgränsförhållanden behöver fördelningen av alla flödesvariabler specificeras , främst flödeshastighet . Detta kan ses som en konjunktion till inloppets gränsvillkor. Denna typ av randvillkor är vanliga och specificeras mest där utloppshastigheten är känd. Flödet uppnår ett fullt utvecklat tillstånd där ingen förändring sker i flödesriktningen när utloppet väljs långt bort från de geometriska störningarna. I ett sådant område kan ett utlopp skisseras och gradienten för alla variabler kan likställas med noll i flödesriktningen utom trycket .

Halkfritt gränsvillkor

Visar väggens gränstillstånd

Den vanligaste gränsen som uppstår vid problem med begränsat vätskeflöde är ledningens vägg. Det lämpliga kravet kallas det halkfria gränsvillkoret , där den normala hastighetskomponenten är fixerad till noll, och den tangentiella komponenten sätts lika med väggens hastighet. Det kan strida mot intuitionen, men halkfri villkoret har fastställts i både experiment och teori, dock först efter årtionden av kontroverser och debatt.

V_{\text{normal}}=0

V_{\text{tangential}}=V_{\text{vägg}}

Värmeöverföring genom väggen kan specificeras eller om väggarna anses vara adiabatiska , så ställs värmeöverföringen över väggen till noll.

Q_{\text{Adiabatic Walls}}=0

Konstant tryck randvillkor

Visar gränsvillkor för konstant tryck

Denna typ av gränsvillkor används där gränsvärdena för tryck är kända och de exakta detaljerna för flödesfördelningen är okända. Detta inkluderar främst tryckinlopps- och utloppsförhållanden. Typiska exempel som utnyttjar detta gränsvillkor inkluderar flytkraftsdrivna flöden, interna flöden med flera utlopp, fria ytflöden och externa flöden runt föremål. Ett exempel är flödesutlopp till atmosfären där trycket är atmosfäriskt.

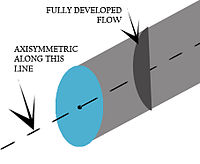
Axisymmetriska randvillkor

Visar axisymmetriskt gränsvillkor

I detta gränstillstånd är modellen axelsymmetrisk med avseende på huvudaxeln så att vid en viss r = R , alla θ s och varje z = Z-skiva, har varje flödesvariabel samma värde. Ett bra exempel är flödet i ett cirkulärt rör där flödet och röraxeln sammanfaller.

${\displaystyle V_{r}(R,\theta ,Z)=Konstant} ($ $\displaystyle (r =R,\theta ,Z)}$

Symmetriskt randvillkor

Visar symmetriska gränsvillkor

I detta gränstillstånd antas det att på de två sidorna av gränsen finns samma fysiska processer. Alla variabler har samma värde och gradienter på samma avstånd från gränsen. Den fungerar som en spegel som reflekterar all flödesfördelning till andra sidan. Villkoren vid symmetrisk gräns är inget flöde över gränsen och inget skalärt flöde över gränsen.

Ett bra exempel är ett rörflöde med ett symmetriskt hinder i flödet. Hindret delar upp det övre flödet och det nedre flödet som speglat flöde.

Periodiskt eller cykliskt gränsvillkor

En fjärdedel som visar cykliskt randvillkor

Ett periodiskt eller cykliskt randvillkor uppstår från en annan typ av symmetri i ett problem. Om en komponent har ett upprepat mönster i flödesfördelning mer än två gånger, vilket bryter mot spegelbildskraven som krävs för symmetriska gränsvillkor. Ett bra exempel skulle vara svept skovelpump (Fig.), där det markerade området upprepas fyra gånger i r-theta-koordinater. De cykliskt-symmetriska områdena bör ha samma flödesvariabler och fördelning och bör uppfylla det i varje Z-skiva.

Se även

Anteckningar

Versteeg (1995). "Kapitel 9". En introduktion till Computational Fluid Dynamics The Finite Volume Method, 2/e . Longman Scientific & Technical. s. 192–206. ISBN 0-582-21884-5 .