Poängregel

Visualisering av förväntad poäng under olika förutsägelser från några vanliga poängfunktioner. Streckad svart linje: prognosmakarens sanna övertygelse, röd: linjär, orange: sfärisk, lila: kvadratisk, grön: stock.

I beslutsteorin ger en poängregel ett sammanfattande mått för utvärdering av probabilistiska förutsägelser eller prognoser . Den är tillämpbar på uppgifter där förutsägelser tilldelar sannolikheter till händelser, dvs man utfärdar en sannolikhetsfördelning $F$ som förutsägelse. Detta inkluderar probabilistisk klassificering av en uppsättning ömsesidigt uteslutande resultat eller klasser .

Å andra sidan ger en poängfunktion ett sammanfattande mått för utvärdering av punktförutsägelser, dvs man förutsäger en egenskap eller funktionell $T(F)$ , som förväntan eller medianen .

Poängregler och poängfunktioner kan ses som "kostnadsfunktion" eller " förlustfunktion ". De utvärderas som empiriskt medelvärde av ett givet urval, helt enkelt kallat poäng. Mängder av olika förutsägelser eller modeller kan sedan jämföras för att komma fram till vilken modell som är bäst.

Om en kostnad tas ut i proportion till en korrekt poängregel, motsvarar den minimala förväntade kostnaden att rapportera den sanna uppsättningen sannolikheter. Korrekt poängregler används i meteorologi, finans och mönsterklassificering där en prognosmakare eller algoritm försöker minimera medelpoängen för att ge raffinerade, kalibrerade sannolikheter (dvs. exakta sannolikheter).

Definition

Betrakta ett exempelrymd $\Omega$ , en σ-algebra ${\mathcal {A}}$ av delmängder av $\Omega$ och en konvex klass ${\mathcal { F}}$ av sannolikhetsmått på $(\Omega ,{\mathcal {A}})$ . En funktion definierad på $\Omega$ och tar värden i den utökade reella linjen, ${\overline {\mathbb {R} }}=[-\infty ,\ infty ]$ , är ${\mathcal {F}}$ -kvasiintegrerbar om den är mätbar med avseende på ${\mathcal {A}}$ och är kvasiintegrerbar med avseende på alla $F\in {\mathcal {F}}$ .

Probabilistisk prognos

En probabilistisk prognos är vilket sannolikhetsmått som helst $F\in {\mathcal {F}}$ .

Poängregel

En poängregel är vilken som helst utökad funktion med verkligt värde ${\displaystyle \mathbf {S} :{\mathcal {F}}\times \Omega \rightarrow \mathbb {R} } så$ att $\mathbf {S} (F,\cdot )$ är ${\mathcal {F}}$ -kvasiintegrerbar för alla $F\in {\mathcal { F}}$ . $\mathbf {S} (F,y)$ representerar förlusten eller straffavgiften när prognosen $F\in {\mathcal {F}}$ utfärdas och observationen $y\in \Omega$ materialiseras.

Punktprognos

En punktprognos är en funktionell, dvs en potentiellt set-valued mappning $F\rightarrow T(F)\subseteq \Omega$ .

Poängfunktion

En poängfunktion är valfri funktion med verkligt värde $S:\Omega \times \Omega \rightarrow \mathbb {R}$ där $S(x,y )$ representerar förlust eller straff när punktprognosen $x\in \Omega$ utfärdas och observationen $y\in \Omega$ materialiseras.

Orientering

Poängregler $\mathbf {S} (F,y)$ och poängfunktioner $S(x,y)$ är negativt (positivt) orienterade om de är mindre ( större) värden betyder bättre. Här håller vi oss till negativ orientering, därav associationen till "förlust".

Exempel medelpoäng

Givet ett exempel $y_{i},i=1\ldots n$ och motsvarande prognoser $F_{i}$ eller $x_{i}$ (t.ex. prognoser från en enda modell), beräknar man medelpoängen som

{\bar {\mathbf {S} }}={\frac {1}{n}}\sum _{i}\mathbf {S } (F_{i},y_{i})

eller

{\bar {S}}={\frac {1}{n}}\summa _{i}S(x_{i},y_ {i})

Genomsnittliga poäng används för att jämföra och rangordna olika prognoser eller modeller.

Anständighet och konsekvens

Strikt korrekta poängregler och strikt konsekventa poängfunktioner uppmuntrar ärliga prognoser genom att maximera den förväntade belöningen: Om en prognosmakare ges en belöning på $-\mathbf {S} (F,y)$ om $y$ realiserar (t.ex. $y=rain$ ), då erhålls den högsta förväntade belöningen (lägsta poängen) genom att rapportera den sanna sannolikhetsfördelningen.

Korrekt poängregler

Vi skriver för förväntad poäng under $Q\in {\mathcal {F}}$

\mathbf {S} (F,Q)=\int \mathbf {S} (F,\omega )\mathrm {d } Q(\omega )

En poängregel $\mathbf {S}$ är korrekt i förhållande till ${\mathcal {F}}$ if (förutsatt negativ orientering)

\mathbf {S} (Q,Q)\leq \mathbf {S} (F,Q)

för alla

F ,Q\in {\mathcal {F}}

.

Det är helt korrekt om ovanstående ekvation gäller med likhet om och endast om $F=Q$ .

Konsekventa poängfunktioner

En poängfunktion $S$ är konsekvent för det funktionella $T$ i förhållande till klassen ${\mathcal {F}}$ om

\operatörsnamn {E} _{F}[S(t,Y)]\leq \operatörsnamn {E} _{F}[S(x,Y)]

för alla

F\in {\mathcal {F}}

, alla

t\in T(F)

och alla

x\in \Omega

.

Det är strikt konsekvent om det är konsekvent och likhet i ovanstående ekvation innebär att $x\in T(F)$ .

Exempel på tillämpning av poängregler

Den logaritmiska regeln

Ett exempel på probabilistisk prognos är i meteorologi där en väderprognos kan ge sannolikheten för regn nästa dag. Man kunde notera antalet gånger som en 25% sannolikhet citerades, under en lång period, och jämföra detta med den faktiska andelen gånger som regn föll. Om den faktiska procenten skilde sig väsentligt från den angivna sannolikheten säger vi att prognosmakaren är dåligt kalibrerad . En dåligt kalibrerad prognosmakare kan uppmuntras att göra bättre ifrån sig av ett bonussystem . Ett bonussystem utformat kring en korrekt poängregel kommer att uppmuntra prognosmakaren att rapportera sannolikheter som motsvarar hans personliga övertygelse .

Förutom det enkla fallet med ett binärt beslut , som att tilldela sannolikheter till "regn" eller "inget regn", kan poängregler användas för flera klasser, som "regn", "snö" eller "klart", eller kontinuerliga svar som mängden regn per dag.

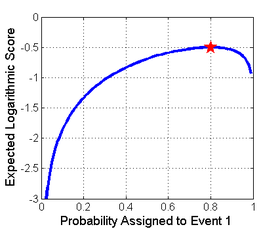
Bilden till höger visar ett exempel på en poängregel, den logaritmiska poängregeln, som en funktion av den sannolikhet som rapporterats för den händelse som faktiskt inträffade. Ett sätt att använda denna regel skulle vara som en kostnad baserat på sannolikheten som en prognosmakare eller algoritm tilldelar, och sedan kontrollera vilken händelse som faktiskt inträffar.

Exempel på korrekta poängregler

Förväntat värde på logaritmisk regel, när händelse 1 förväntas inträffa med sannolikheten 0,8

Det finns ett oändligt antal poängregler, inklusive hela parametriserade familjer av strikt korrekta poängregler. De som visas nedan är helt enkelt populära exempel.

Kategoriska variabler

För en kategorisk svarsvariabel med $m$ ömsesidigt uteslutande händelser, ${\displaystyle Y\in \Omega =\{1,\ldots ,m\}} ,$ en probabilistisk prognostiserare eller algoritm kommer att returnera en sannolikhetsvektor $\mathbf {r}$ med en sannolikhet för vart och ett av de $m$ -utfallen.

Logaritmisk poäng

Den logaritmiska poängregeln är en lokal strikt korrekt poängregel. Detta är också det negativa med överraskning , som vanligtvis används som ett poängkriterium i Bayesiansk slutledning ; målet är att minimera förväntad överraskning. Denna poängregel har en stark grund i informationsteori .

{\displaystyle L(\mathbf {r} ,i)=\ln(r_{i})

Här beräknas poängen som logaritmen av sannolikhetsuppskattningen för det faktiska utfallet. Det vill säga, en förutsägelse på 80 % som korrekt visade sig vara sann skulle få poängen $ln(0,8) = -0,22$ . Samma förutsägelse tilldelar också 20% sannolikhet till det motsatta fallet, så om förutsägelsen visar sig vara falsk, skulle den få en poäng baserad på 20%: $ln(0.2) = -1.6$ . Målet för en prognosmakare är att maximera poängen och att poängen ska vara så stor som möjligt, och -0,22 är verkligen större än -1,6.

Om man behandlar sanningen eller falskheten i förutsägelsen som en variabel $x$ med värdet 1 respektive 0, och den uttryckta sannolikheten som $p$ , så kan man skriva den logaritmiska poängregeln som $x ln(p) + (1 - x) ln( 1 - p)$ . Observera att vilken logaritmisk bas som helst kan användas, eftersom strikt korrekta poängregler förblir strikt korrekta under linjär transformation. Det är:

L(\mathbf {r} ,i)=\log _{b}(r_{i})

är strikt lämplig för alla $b>1$ .

Brier/Kvadratisk poäng

Den kvadratiska poängregeln är en strikt korrekt poängregel

Q(\mathbf {r} ,i)=2r_{i}-\mathbf {r } \cdot \mathbf {r} =2r_{i}-\sum _{j=1}^{C}r_{j}^{2}

där $r_{i}$ är sannolikheten som tilldelas det korrekta svaret och $C$ är antalet klasser.

Brier -poängen , som ursprungligen föreslogs av Glenn W. Brier 1950, kan erhållas genom en affin transformation från den kvadratiska poängregeln.

B(\mathbf {r} ,i)=\summa _{j=1}^{C}(y_{j }-r_{j})^{2}

Där $y_{j}=1$ när $j$ :e händelsen är korrekt och $y_{j}=0$ annars och $C$ är antalet klasser.

En viktig skillnad mellan dessa två regler är att en prognosmakare bör sträva efter att maximera den kvadratiska poängen $Q$ men ändå minimera Brier-poängen $B$ . Detta beror på ett negativt tecken i den linjära transformationen mellan dem.

Hyvärinen poängregel

Hyvärinen poängfunktion (av en densitet p) definieras av

s(p)=2\Delta _{y}\log p(y)+\ |\nabla _{y}\log p(y)\|_{2}^{2}

Där $\Delta$ anger det hessiska spåret och $\nabla$ anger gradienten . Denna poängregel kan användas för att beräkningsmässigt förenkla parameterinferens och adressera bayesiansk modelljämförelse med godtyckligt vaga tidigare. Det användes också för att introducera nya informationsteoretiska storheter utöver den befintliga informationsteorin .

Sfärisk poäng

Den sfäriska poängregeln är också en strikt korrekt poängregel

S(\mathbf {r} ,i)={\frac {r_{i}}{\lVert \mathbf {r} \rVert }}={\frac {r_{i}}{\sqrt {r_{1}^{2}+\cdots +r_{c}^{2}}}}

Kontinuerliga variabler

Kontinuerlig rankad sannolikhetspoäng

Den kontinuerliga rankade sannolikhetspoängen (CRPS) är en strikt korrekt poängregel som ofta används inom meteorologi. Det definieras som

$CRPS(F,y)=\int _{\mathbb {R} }(F (x)-\mathbb {1} (x\geq y))^{2}dx$

där F är den prognostiserade kumulativa fördelningsfunktionen och $y\in \mathbb {R}$ är observationen.

Tolkning av korrekta poängregler

Alla korrekta poängregler är lika med viktade summor (integral med en icke-negativ viktningsfunktion) av förlusterna i en uppsättning enkla två-alternativa beslutsproblem som använder den probabilistiska förutsägelsen, där varje sådant beslutsproblem har en speciell kombination av associerade kostnadsparametrar för falskt positiva och falskt negativa beslut. En strikt korrekt poängregel motsvarar att ha en viktning som inte är noll för alla möjliga beslutströsklar. Varje given korrekt poängregel är lika med de förväntade förlusterna med avseende på en viss sannolikhetsfördelning över beslutströskelvärdena; sålunda motsvarar valet av en poängregel ett antagande om sannolikhetsfördelningen av beslutsproblem för vilka de förutsagda sannolikheterna i slutändan kommer att användas, med till exempel den kvadratiska förlusten (eller Brier) poängregeln som motsvarar en enhetlig sannolikhet för att beslutströskeln är någonstans mellan noll och ett. Klassificeringsnoggrannhetspoängen (procenten klassificeras korrekt), en poängregel med en enda tröskel som är noll eller ett beroende på om den förutsagda sannolikheten är på den lämpliga sidan av 0,5, är en korrekt poängregel men inte en strikt korrekt poängregel eftersom den är optimeras (i förväntan) inte bara genom att förutsäga den sanna sannolikheten utan genom att förutsäga vilken sannolikhet som helst på samma sida av 0,5 som den sanna sannolikheten.

Jämförelse av strikt korrekta poängregler

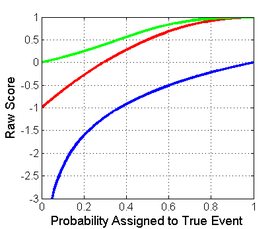
Nedan till vänster visas en grafisk jämförelse av logaritmiska, kvadratiska och sfäriska poängregler för ett binärt klassificeringsproblem. X -axeln indikerar den rapporterade sannolikheten för den händelse som faktiskt inträffade .

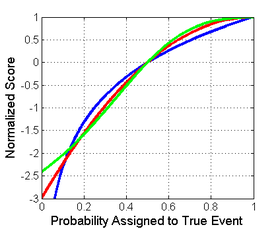
Det är viktigt att notera att varje poäng har olika storlek och placering. Storleksskillnaderna är dock inte relevanta eftersom poängen förblir korrekta under affin transformation. För att jämföra olika poäng är det därför nödvändigt att flytta dem till en gemensam skala. Ett rimligt val av normalisering visas på bilden till höger där alla poäng skär punkterna (0,5,0) och (1,1). Detta säkerställer att de ger 0 för en enhetlig fördelning (två sannolikheter på 0,5 vardera), vilket återspeglar ingen kostnad eller belöning för att rapportera vad som ofta är baslinjefördelningen. Alla normaliserade poäng nedan ger också 1 när den sanna klassen tilldelas en sannolikhet på 1.

Poäng för en binär klassificering för den sanna klassen som visar logaritmisk (blå), sfärisk (grön) och kvadratisk (röd)

Normaliserad poäng för en binär klassificering för den sanna klassen som visar logaritmisk (blå), sfärisk (grön) och kvadratisk (röd)

Egenskaper

Affin transformation

En strikt korrekt poängregel, oavsett om den är binär eller multiklassig, efter en affin transformation förblir en strikt korrekt poängregel. Det vill säga, om ${r} ,i)}$ $a+bS(\mathbf { r} ,i)$ är en strikt korrekt poängregel då med $b\neq 0$ är också en strikt korrekt poängregel, men om $b<0$ så växlar optimeringskänslan för poängregeln mellan maximering och minimering.

Lokalitet

En korrekt poängregel sägs vara lokal om dess uppskattning av sannolikheten för en specifik händelse endast beror på sannolikheten för den händelsen. Detta påstående är vagt i de flesta beskrivningar men vi kan i de flesta fall tänka på detta som att den optimala lösningen av poängproblemet "vid en specifik händelse" är oförändrad till alla förändringar i observationsfördelningen som lämnar sannolikheten för den händelsen oförändrad. Alla binära poäng är lokala eftersom sannolikheten som tilldelas händelsen som inte inträffade bestäms så det finns ingen grad av flexibilitet att variera över.

Affina funktioner i den logaritmiska poängregeln är de enda strikt korrekta lokala poängreglerna på en finit uppsättning som inte är binär.

Sönderfall

Förväntningsvärdet för en korrekt poängregel $S$ kan delas upp i summan av tre komponenter, kallade osäkerhet , tillförlitlighet och upplösning , som kännetecknar olika attribut för probabilistiska prognoser:

E(S)=\mathrm {UNC} +\mathrm {REL} -\mathrm {RES} .

Om en poäng är korrekt och negativt orienterad (som Brier-poängen), är alla tre termer positiva definitiva. Osäkerhetskomponenten är lika med den förväntade poängen för prognosen som ständigt förutsäger den genomsnittliga händelsefrekvensen. Tillförlitlighetskomponenten straffar dåligt kalibrerade prognoser, där de förutsagda sannolikheterna inte sammanfaller med händelsefrekvenserna.

Ekvationerna för de individuella komponenterna beror på den specifika poängregeln. För Brier-poängen ges de av

\mathrm {UNC} ={\bar {x}}(1-{\bar {x}})

\mathrm {REL} =E(p-\pi (p))^{2}

\mathrm {RES } =E(\pi (p)-{\bar {x}})^{2}

där ${\bar {x}}$ är den genomsnittliga sannolikheten för att den binära händelsen ${\displaystyle x} ska inträffa$ , och $\pi (p)$ är den villkorade händelsesannolikheten , givet $p$ , dvs $\pi (p)=P(x=1\mid p)$

Se även

externa länkar