Plan algebra

Inom matematiken dök plana algebror först upp i Vaughan Jones arbete på standardinvarianten av en II ₁ subfaktor - . De tillhandahåller också ett lämpligt algebraiskt ramverk för många knutinvarianter (särskilt Jones-polynomet ), och har använts för att beskriva egenskaperna hos Khovanov-homologi med avseende på härvors sammansättning. Vilken plan algebra som helst ger en familj av enhetliga representationer av Thompson-grupper . Vilken finit grupp som helst (och kvantgeneralisering) kan kodas som en plan algebra.

Definition

Tanken med den plana algebra är att vara en schematisk axiomatisering av standardinvarianten .

Plan härva

En (skuggad) plan härva är data för ändligt många ingångsskivor , en utdataskiva , icke-korsande strängar som ger ett jämnt tal, säg $2n$ , intervaller per skiva och en $\star$ - markerat intervall per skiva.

Här visas märket som en $\star$ -form. På varje ingångsskiva placeras den mellan två intilliggande utgående strängar, och på utgångsskivan placeras den mellan två intilliggande inkommande strängar. En plan härva definieras upp till isotopi .

Sammansättning

För att komponera två plana härvor, placera utdataskivan för den ena i en ingång till den andra, med lika många intervall, samma skuggning av markerade intervall och så att de ⋆ {\displaystyle \star } -markerade $sammanfaller$ . Till sist tar vi bort de sammanfallande cirklarna. Observera att två plana tovor kan ha noll, en eller flera möjliga sammansättningar.

Planar operad

Den plana operad är uppsättningen av alla plana härvor (upp till isomorfism) med sådana kompositioner.

Plan algebra

En plan algebra är en representation av den plana operad; mer exakt är det en familj av vektorrum $({\mathcal {P}}_{n,\pm })_{n\in \mathbb {N} }$ , kallade $n$ -boxutrymmen, på vilka verkar den plana operad, dvs för valfri härva $T$ (med en utgångsskiva och $r$ ingångsskivor med $2n_ {0}$ och $2n_{1},\dots ,2n_{r}$ intervaller) det finns en multilinjär karta

$Z_{T}:{\mathcal {P}}_{n_{1},\epsilon _{1 }}\otimes \cdots \otimes {\mathcal {P}}_{n_{r},\epsilon _{r}}\to {\mathcal {P}}_{n_{0},\epsilon _{0 }}$

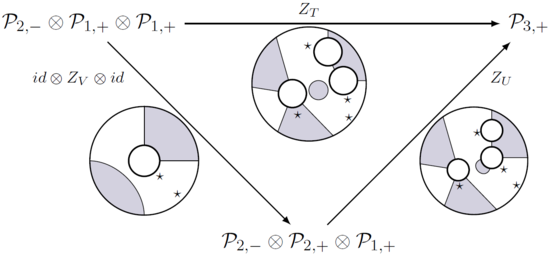
med $\epsilon _{i}\in \{+,-\}$ enligt skuggningen av de $\star$ -markerade intervallen, och dessa kartor (även kallas partitionsfunktioner) respekterar härvans sammansättning på ett sådant sätt att alla diagram som nedan pendlar.

Exempel

Plana tovor

Familjen vektorrum $({\mathcal {T}}_{n,\pm })_{n\in \mathbb {N} }$ genererad av de plana tovorna med $2n$ -intervall på sin utdataskiva och ett vitt (eller svart) $\star$ -markerat intervall, tillåter en plan algebrastruktur.

Temperley–Lieb

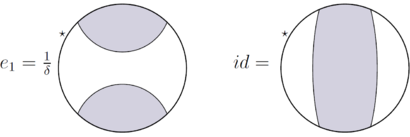
Temperley-Lieb plana algebra ${\mathcal {TL}}(\delta )$ av de plana tovorna utan ingångsskiva; dess $3$ -boxutrymme ${\mathcal {TL}}_{3,+}(\delta )$ genereras av

Dessutom ersätts en sluten sträng av en multiplikation med $\delta$ .

Observera att dimensionen för ${\mathcal {TL}}_{n,\pm }(\delta )$ är det katalanska talet ${\ displaystyle {\frac {1}{n+1}}{\binom {2n}{n}}}$ . Denna plana algebra kodar begreppet Temperley–Lieb algebra .

Hopp algebra

En semisenkel och kosseminkel Hopf-algebra över ett algebraiskt stängt fält kodas i en plan algebra definierad av generatorer och relationer, och "motsvarar" (upp till isomorfism) en sammankopplad, irreducerbar, sfärisk, icke degenererad plan algebra med en modul som inte är noll ${ \displaystyle \delta }$ och av djup två.

Observera att ansluten betyder ${\displaystyle \dim({\mathcal {P}}_{0,\pm })=1} ($ som för utvärderingsbar nedan), irreducible betyder ${\displaystyle \dim({\mathcal {P}}_{1,+})=1} ,$ sfärisk definieras nedan och icke-degenererad betyder att spåren (definierade nedan) är icke- degenererad.

Subfaktor plan algebra

Definition

En subfaktor plan algebra är en plan $\star$ -algebra $({\mathcal {P}}_{n,\pm })_{n\in \ mathbb {N} }$ vilket är:

(1) Ändlig dimensionell: $\dim({\mathcal {P}}_{n,\pm })<\infty$

(2) Utvärderbar: ${\displaystyle {\mathcal {P}}_{0,\pm }=\mathbb {C} } ($

3) Sfärisk: $tr:=tr_{ r}=tr_{l}$

(4) Positiv: $\langle a\vert b\rangle =tr(b^{\star }a)$ definierar en inre produkt.

Observera att med (2) och (3) räknas alla slutna strängar (skuggade eller inte) för samma konstant $\delta$ .

Tangle action handlar om adjoint genom att:

$Z_{T}(a_{_1} 2}\otimes \cdots \otimes a_{r})^{\star }=Z_{T^{\star }}(a_{1}^{\star }\otimes a_{2}^{\star }\ ibland \cdots \otimes a_{r}^{\star })$

med $T^{\star }$ spegelbilden av $T$ och $a_{i}^{\star }$ adjointen till $a_{ i}$ i ${\mathcal {P}}_{n_{i},\epsilon _{i}}$ .

Exempel och resultat

No-ghost theorem : Den plana algebra ${\mathcal {TL}}(\delta )$ har inget spöke (dvs element $a$ med $\langle a\vert a\rangle <0$ ) if and only if

$\delta \in \{2\cos(\pi /n)|n=3,4,5,...\}\cup [2,+\infty ]$

För $\delta$ enligt ovan, låt ${\mathcal {I}}$ vara nollidealet (genererat av elementen $a$ med $\langle a\vert a\rangle =0$ ). Då är kvoten ${\mathcal {TL}}(\delta )/{\mathcal {I}}$ en subfaktor plan algebra, kallad Temperley–Lieb-Jones subfaktor planar algebra ${\mathcal {TLJ}}(\delta)$ . Vilken subfaktor som helst plan algebra med konstant $\delta$ tillåter ${\mathcal {TLJ}}(\delta )$ som plan subalgebra.

En plan algebra $({\mathcal {P}}_{n,\pm })$ är en subfaktor plan algebra om och endast om den är standardinvarianten för en extremal subfaktor $N\subseteq M$ av index $[M:N]=\delta ^{2}$ , med ${\ displaystyle {\mathcal {P}}_{n,+}=N'\cap M_{n-1}}$ och ${\mathcal {P}}_{n ,-}=M'\cap M_{n}$ . Ett ändligt djup eller irreducerbar subfaktor är extremal ( $tr_{N'}=tr_{M}$ på $N'\cap M$ ).

Det finns en subfaktor plan algebra som kodar vilken ändlig grupp som helst (och mer allmänt, vilken ändlig dimensionell Hopf ${\displaystyle {\rm {C}}}^{\star }} som helst$ -algebra , kallad Kac-algebra, definierad av generatorer och relationer . En (ändlig dimensionell) Kac-algebra "motsvarar" (upp till isomorfism) en irreducerbar subfaktor plan algebra av djup två.

Subfaktorn plana algebra associerad med en inkludering av finita grupper, kommer inte alltid ihåg den (kärnfria) inneslutningen.

En Bisch-Jones subfaktor plan algebra ${\mathcal {BJ}}(\delta _{1},\delta _{2})$ (ibland kallad Fuss-Catalan) är definieras som för ${\mathcal {TLJ}}(\delta )$ men genom att tillåta två färger av sträng med sin egen konstant $\delta _{1}$ och $\delta _{2}$ , med $\delta _{i}$ enligt ovan. Det är en plan subalgebra av vilken subfaktor som helst plan algebra med en mellanliggande sådan att $[K:N]=\delta _{1}^{2}$ och $[M:K]=\delta _{2}^{2}$ .

Den första plana algebra för finita djupsubfaktorer med index $\delta ^{2}>4$ kallas Haagerup -subfaktorns plana algebra. Den har index $(5+{\sqrt {13}})/2\sim 4.303$ .

Underfaktorns plana algebror är helt klassificerade för index högst $5$ och en bit bortom. Denna klassificering initierades av Uffe Haagerup . Den använder (bland annat) en lista över möjliga huvudgrafer, tillsammans med inbäddningssatsen och manetalgoritmen.

En subfaktor plan algebra kommer ihåg subfaktorn (dvs dess standardinvariant är komplett) om den är mottaglig. En hyperfinit subfaktor med ändligt djup är mottaglig.

Om det icke mottagliga fallet: det finns oklassificerbart många irreducerbara hyperfinita subfaktorer av index 6 som alla har samma standardinvariant.

Fouriertransform och biprojektioner

Låt $N\delmängd M$ vara en finit indexsubfaktor, och ${\mathcal {P}}$ motsvarande planalgebra för subfaktorn. Antag att ${\mathcal {P}}$ är irreducerbar (dvs ${\mathcal {P}}_{1,+}=N'\ cap M_{1}=\mathbb {C}$ ). Låt $N\delmängd K\delmängd M$ vara en mellanliggande delfaktor. Låt Jones projicera $e_{K}^{M}:L^{2}(M)\to L^{2}(K)$ . Observera att $e_{K}^{M}\in {\mathcal {P}}_{2,+}$ . Låt $id:=e_{M}^{M}$ och $e_{1}:=e_{N}^{M}$ .

Observera att $tr(e_{1})=\delta ^{-2}=[M:N]^{-1}$ och $tr(id)=1$ .

Låt den bijektiva linjära kartan ${\mathcal {F}}:{\mathcal {P}}_{2,\pm }\to {\mathcal {P}} _{2,\mp }$ vara Fouriertransformen , även kallad $1$ -klick (av den yttre stjärnan) eller $90^{\circ }$ rotation; och låt $a*b$ vara samprodukten av $a$ och $b$ .

Observera att ordet samprodukt är en diminutiv av faltningsprodukt . Det är en binär operation.

Samprodukten uppfyller likheten $a*b={\mathcal {F}}({\mathcal {F}}^{-1}(a){\mathcal {F}}^{-1}(b)).$

För alla positiva operatorer $a,b$ , är samprodukten $a*b$ också positiv; detta kan ses schematiskt:

Låt ${\displaystyle {\overline {a}}:={\mathcal {F}}({\mathcal {F}}}(a))} vara$ motsättningen a $\ displaystyle a}$ (även kallad $180^{\circ }$ rotation). Kartan ${\mathcal {F}}^{4}$ motsvarar fyra $1$ -klick på den yttre stjärnan, så det är identitetskartan, och sedan ${\ displaystyle {\overline {\overline {a}}}=a}$ .

I Kac-algebrafallet är motsatsen exakt antipoden, som för en finit grupp motsvarar det omvända.

En biprojektion är en projektion $b\in {\mathcal {P}}_{2,+}\setminus \{0\}$ med ${ \mathcal {F}}(b)$ en multipel av en projektion. Observera att $e_{1}=e_{N}^{M}$ och $id=e_{M}^{M}$ är biprojektioner; detta kan ses på följande sätt:

En projektion $b$ är en biprojektion om det är Jones-projektionen $e_{K}^{M}$ av en mellanliggande subfaktor $N\subset K\subset M$ , iff $e_{1}\leq b={\överlinje {b}}=\lambda b *b,{\text{ med }}\lambda ^{-1}=\delta tr(b)$ .

Galois-överensstämmelse : i Kac-algebrafallet är biprojektionerna 1-1 med de vänstra koideala subalgebrerna, som för en finit grupp motsvarar undergrupperna.

För varje irreducerbar subfaktor plan algebra är uppsättningen av biprojektioner ett finit gitter, av formen $[e_{1},id]$ , som för ett intervall av finita grupper $[H,G]$ .

Med hjälp av biprojektionerna kan vi göra den mellanliggande subfaktorn plana algebror.

Osäkerhetsprincipen sträcker sig till alla irreducerbara subfaktorer plan algebra ${\mathcal {P}$ } :

Låt ${\mathcal {S}}(x)=Tr(R(x))$ med ${\displaystyle R(x)$ } områdesprojektion av $x$ och $Tr$ det onormaliserade spåret (dvs. $Tr=\delta ^{n}tr$ på ${\displaystyle {\mathcal {P}}_{n,\pm }})$ .

Icke-kommutativ osäkerhetsprincip : Låt ${\displaystyle x\in {\mathcal {P}}_{2,\pm }} ,$ icke noll. Sedan

${\mathcal {S}}(x){\mathcal {S}}({\mathcal {F}}(x))\geq \delta ^{2}$

Om vi ​​antar $x$ och ${\mathcal {F}}(x)$ positiva, gäller likheten om och endast om $x$ är en biprojektion. Mer generellt gäller likheten om och endast om $x$ är bi-förskjutningen av en biprojektion.