Pinch (plasmafysik)
En nypa (eller: Bennett pinch (efter Willard Harrison Bennett ), elektromagnetisk pinch , magnetic pinch , pinch effect , eller plasma pinch .) är kompressionen av en elektriskt ledande glödtråd av magnetiska krafter, eller en anordning som gör det. Ledaren är vanligtvis ett plasma , men kan också vara en fast eller flytande metall . Nypor var den första typen av anordning som användes för experiment med kontrollerad kärnfusionskraft .
Nyper uppstår naturligt i elektriska urladdningar såsom blixtar , planetariska norrsken , strömskivor och solflammor .
Grundläggande mekanism
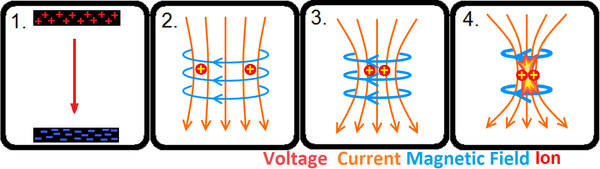
Typer

Nypor finns i naturen och i laboratorier. Nypor skiljer sig åt i sin geometri och arbetskrafter. Dessa inkluderar:
- Okontrollerad – Varje gång en elektrisk ström rör sig i stora mängder (t.ex. blixtar, bågar, gnistor, urladdningar) kan en magnetisk kraft dra ihop plasma. Detta kan vara otillräckligt för fusion.
- Arknypa – En astrofysisk effekt, som uppstår från stora ark av laddade partiklar.
- Z-pinch - Strömmen går längs axeln, eller väggarna, av en cylinder medan magnetfältet är azimutalt
- Theta pinch - Det magnetiska fältet löper längs en cylinders axel, medan det elektriska fältet är i azimutriktningen ( även kallad tetatron)
- Screw pinch - En kombination av en Z-pinch och theta pinch (även kallad en stabiliserad Z-nyp, eller θ-Z pinch)
- Reversed field pinch eller toroidal pinch – Detta är en Z-nypa arrangerad i form av en torus . Plasman har ett inre magnetfält. När avståndet ökar från mitten av denna ring, ändrar magnetfältet riktning.
- Invers pinch – Ett tidigt fusionskoncept, denna enhet bestod av en stav omgiven av plasma. Ström färdades genom plasman och återvände längs mittstaven. Denna geometri var något annorlunda än en z-nypa genom att ledaren var i mitten, inte sidorna.
- Cylindrisk nypa
- Ortogonal nypeffekt
- Ware pinch – En nypa som uppstår inuti en Tokamak-plasma, när partiklar i banans omloppsbana kondenserar samman.
- Magnetized Liner Inertial Fusion (MagLIF) – En Z-nypa förvärmt, förmagnetiserat bränsle inuti ett metallfoder, vilket kan leda till antändning och praktisk fusionsenergi med en större drivkraft med pulserande kraft.
Vanligt beteende
Nyper kan bli instabila . De strålar ut energi över hela det elektromagnetiska spektrumet inklusive radiovågor , mikrovågor , infraröd , röntgenstrålning , gammastrålning , synkrotronstrålning och synligt ljus . De producerar också neutroner , som en produkt av fusion.
Applikationer och enheter
Nypor används för att generera röntgenstrålar och de intensiva magnetfält som genereras används vid elektromagnetisk formning av metaller. De har också tillämpningar i partikelstrålar inklusive partikelstrålevapen, astrofysikstudier och det har föreslagits att använda dem i rymdframdrivning. Ett antal stora klämmaskiner har byggts för att studera fusionskraft ; här är flera:
- MAGPIE En Z-nypa på Imperial College. Detta dumpar en stor mängd ström över en tråd. Under dessa förhållanden blir tråden plasma och komprimeras för att producera fusion.
- Z Pulsed Power Facility vid Sandia National Laboratories.
- ZETA- enhet i Culham, England
- Madison Symmetric Torus vid University of Wisconsin, Madison
- Omvänt fältexperiment i Italien.
- tät plasmafokus i New Jersey
- University of Nevada, Reno (USA)
- Cornell University (USA)
- University of Michigan (USA)
- University of California, San Diego (USA)
- University of Washington (USA)
- Ruhr-universitetet (Tyskland)
- École Polytechnique (Frankrike)
- Weizmann Institute of Science (Israel)
- Universidad Autónoma Metropolitana (Mexiko).
- Zap Energy Inc. (USA)
Krossande burkar med nypeffekten
Många högspänningselektronikentusiaster tillverkar sina egna råa elektromagnetiska formningsanordningar. De använder pulserande krafttekniker för att producera en theta-nypa som kan krossa en läskburk av aluminium med hjälp av Lorentz-krafterna som skapas när stora strömmar induceras i burken av primärspolens starka magnetfält.
aluminiumburkkross består av fyra huvudkomponenter: en högspänningslikströmskälla , som tillhandahåller en källa till elektrisk energi , en stor energiurladdningskondensator för att ackumulera den elektriska energin, en högspänningsomkopplare eller gnistgap och en robust spole (kapabel att överleva högt magnetiskt tryck) genom vilket den lagrade elektriska energin snabbt kan urladdas för att generera ett motsvarande starkt nypande magnetfält (se diagram nedan).
I praktiken är en sådan enhet något mer sofistikerad än vad det schematiska diagrammet antyder, inklusive elektriska komponenter som styr strömmen för att maximera den resulterande nypningen och för att säkerställa att enheten fungerar säkert. För mer information, se anteckningarna.
Historia

Den första skapandet av en Z-nypa i laboratoriet kan ha inträffat 1790 i Holland när Martinus van Marum skapade en explosion genom att släppa ut 100 Leyden-burkar i en tråd. Fenomenet förstods inte förrän 1905, när Pollock och Barraclough undersökte en sammanpressad och förvrängd längd av kopparrör från en blixtstång efter att den hade träffats av blixten. Deras analys visade att krafterna på grund av samverkan mellan det stora strömflödet och dess eget magnetfält kunde ha orsakat kompressionen och distorsionen. En liknande, och till synes oberoende, teoretisk analys av nypeffekten i flytande metaller publicerades av Northrup 1907. Nästa stora utveckling var publiceringen 1934 av en analys av den radiella tryckbalansen i en statisk Z-nypa av Bennett ( se följande avsnitt för detaljer).
Därefter drevs de experimentella och teoretiska framstegen på nypor av fusionskraftforskning . I sin artikel om "Wire-array Z-pinch: a powerful x-ray source for ICF ", MG Haines et al. , skrev om "Early history of Z-pinches".
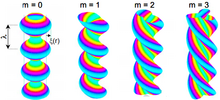
- 1946 lämnade Thompson och Blackman in ett patent för en fusionsreaktor baserad på en toroidformad Z-nypa med ytterligare ett vertikalt magnetfält. Men 1954 publicerade Kruskal och Schwarzschild sin teori om MHD-instabilitet i en Z-nypa. 1956 höll Kurchatov sin berömda Harwell-föreläsning som visade icke-termiska neutroner och närvaron av m = 0 och m = 1 instabiliteter i en deuteriumnypa. 1957 förutspådde Pease och Braginskii oberoende strålningskollaps i en Z-nypa under tryckbalans när strömmen i väte överstiger 1,4 MA. (Den viskösa snarare än den resistiva avledningen av magnetisk energi som diskuterats ovan och in skulle emellertid förhindra strålningskollaps).
År 1958 utfördes världens första kontrollerade termonukleära fusionsexperiment med hjälp av en nypningsmaskin vid namn Scylla I vid Los Alamos National Laboratory . En cylinder full av deuterium omvandlades till en plasma och komprimerades till 15 miljoner grader Celsius under en theta-pinch-effekt. Slutligen, vid Imperial College 1960, ledd av R Latham, visades Plateau–Rayleigh-instabiliteten och dess tillväxthastighet mättes i en dynamisk Z-nypa.
Jämviktsanalys
En dimension
Inom plasmafysik studeras vanligtvis tre nypgeometrier: θ-nypan, Z-nypan och skruvnypan. Dessa är cylindriskt formade. Cylindern är symmetrisk i den axiella ( z ) riktningen och den azimutala (θ) riktningen. De endimensionella nypningarna är namngivna efter den riktning som strömmen rör sig.
θ-nypan
θ-nypan har ett magnetfält riktat i z-riktningen och en stor diamagnetisk ström riktad i θ-riktningen. Med hjälp av Ampères kretslag (bortkasta förskjutningstermen)
Eftersom B endast är en funktion av r kan vi förenkla detta till
Så J pekar i riktningen θ.
Sålunda lyder jämviktsvillkoret ( ) för θ-nypan:
θ-nypor tenderar att vara resistenta mot plasmainstabilitet; Detta beror delvis på Alfvéns sats (även känd som satsen för infryst flöde).
Z-nypan
Z-pinchen har ett magnetfält i θ-riktningen och en ström J som flyter i z -riktningen. Återigen, enligt den elektrostatiska Ampères lag,
Sålunda, jämviktstillståndet, för Z-nypan lyder:
Eftersom partiklar i en plasma i princip följer magnetfältslinjer, leder Z-nypor dem runt i cirklar. Därför tenderar de att ha utmärkta inneslutningsegenskaper.
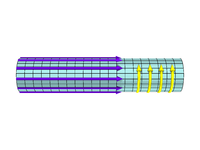
Skruven klämmer
Skruvnypet är ett försök att kombinera stabilitetsaspekterna av θ-nypen och inneslutningsaspekterna av Z-nypen. Återigen hänvisar vi till Ampères lag,
Men den här gången har B- fältet en θ-komponent och en z- komponent
Så den här gången har J en komponent i z -riktningen och en komponent i θ-riktningen.
Slutligen, jämviktsvillkoret ( ) för skruvnypan lyder:
Skruven klämmer via kolliderande optiska virvlar
Skruvnypet kan framställas i laserplasma genom att kollidera med optiska virvlar med ultrakort varaktighet . För detta ändamål bör optiska virvlar vara faskonjugerade. Magnetfältsfördelningen ges här igen via Ampères lag:
Två dimensioner
Ett vanligt problem med endimensionella nypor är ändförlusterna. Det mesta av partiklars rörelse sker längs magnetfältet. Med θ-nypen och skruvnypan leder detta mycket snabbt ut partiklar ur änden av maskinen, vilket leder till en förlust av massa och energi. Tillsammans med detta problem har Z-pinch stora stabilitetsproblem. Även om partiklar kan reflekteras i viss utsträckning med magnetiska speglar , tillåter även dessa många partiklar att passera. En vanlig metod för att övervinna dessa slutförluster är att böja cylindern runt till en torus. Tyvärr bryter detta θ-symmetri, eftersom banorna på den inre delen (inombordssidan) av torusen är kortare än liknande banor på den yttre delen (utombordssidan). Det behövs alltså en ny teori. Detta ger upphov till den berömda Grad–Shafranov-ekvationen . Numeriska lösningar på Grad–Shafranov-ekvationen har också gett en del jämvikter, framför allt den omvända fältnypan .
Tre dimensioner
Från och med 2015 finns det ingen sammanhängande analytisk teori för tredimensionella jämvikter. Det allmänna tillvägagångssättet för att hitta sådana jämvikter är att lösa de vakuumideala MHD-ekvationerna. Numeriska lösningar har gett konstruktioner för stellaratorer . Vissa maskiner drar fördel av förenklingstekniker som spiralsymmetri (till exempel University of Wisconsins Helically Symmetric eXperiment). Men för en godtycklig tredimensionell konfiguration existerar en jämviktsrelation, liknande den för 1-D-konfigurationerna:
Där κ är krökningsvektorn definierad som:
med b enhetsvektorn som tangerar B .
Formell behandling

Bennett-relationen
Betrakta en cylindrisk kolonn av helt joniserad kvasineutral plasma, med ett axiellt elektriskt fält, som producerar en axiell strömtäthet, j , och tillhörande azimutalt magnetfält, B . När strömmen flyter genom sitt eget magnetfält genereras en nypa med en inåtriktad radiell krafttäthet på jx B . I ett stabilt tillstånd med balanserande krafter:
där ∇ p är den magnetiska tryckgradienten, och p e och p i är elektron- respektive jontrycken. Använd sedan Maxwells ekvation och den ideala gaslagen , vi härleder:
- (Bennett-relationen)
där N är antalet elektroner per längdenhet längs axeln, T e och Ti . är elektron- och jontemperaturerna, I är den totala strålströmmen och k är Boltzmann-konstanten
Den generaliserade Bennett-relationen
Den generaliserade Bennett-relationen betraktar en strömförande magnetfältsinriktad cylindrisk plasmanypa som genomgår rotation vid vinkelfrekvensen ω. Längs plasmacylinderns axel flyter en strömtäthet jz, vilket resulterar i ett azimutiskt magnetfält Β φ . Ursprungligen härledd av Witalis, resulterar den generaliserade Bennett-relationen i:
- där ett strömförande, magnetfältsinriktat cylindriskt plasma har en radie a ,
- 0 J är det totala tröghetsmomentet med avseende på z-axeln,
- W ⊥kin är den kinetiska energin per längdenhet på grund av strålens rörelse tvärs strålens axel
- W B z är den självständiga Bz- energin per längdenhet
- W E z är den självständiga Ez- energin per längdenhet
- W k är termokinetisk energi per längdenhet
- I ( a ) är den axiella strömmen innanför radien a ( r i diagrammet)
- N ( a ) är det totala antalet partiklar per längdenhet
- E r är det radiella elektriska fältet
- E φ är det roterande elektriska fältet
De positiva termerna i ekvationen är expansionskrafter medan de negativa termerna representerar strålens kompressionskrafter.
Carlqvistrelationen
Carlqvist-relationen, publicerad av Per Carlqvist 1988, är en specialisering av den generaliserade Bennett-relationen (ovan), för det fall att det kinetiska trycket är mycket mindre vid gränsen av nypet än i de inre delarna. Det tar formen
och är tillämplig på många rymdplasma.

Carlqvist-relationen kan illustreras (se höger), som visar den totala strömmen ( I ) kontra antalet partiklar per längdenhet ( N ) i en Bennett-nypa. Diagrammet illustrerar fyra fysiskt distinkta regioner. Plasmatemperaturen är ganska kall ( T i = T e = T n = 20 K), innehåller huvudsakligen väte med en medelpartikelmassa på 3×10 −27 kg. Den termokinetiska energin W k >> πa 2 p k (a). Kurvorna, ΔW Bz visar olika mängder överskott av magnetisk energi per längdenhet på grund av det axiella magnetfältet Bz . Plasman antas vara icke-roterande, och det kinetiska trycket vid kanterna är mycket mindre än inuti.
Kartregioner: (a) I det övre vänstra området dominerar nypkraften. (b) Mot botten balanserar utåtriktade kinetiska tryck inåt magnetiskt tryck, och det totala trycket är konstant. (c) Till höger om den vertikala linjen Δ W B z = 0, balanserar de magnetiska trycken gravitationstrycket, och klämkraften är försumbar. (d) Till vänster om den lutande kurvan Δ W B z = 0 är gravitationskraften försumbar. Observera att diagrammet visar ett specialfall av Carlqvist-relationen, och om det ersätts av den mer allmänna Bennett-relationen, är de angivna regionerna i diagrammet inte giltiga.
Carlqvist noterar vidare att genom att använda relationerna ovan, och en derivata, är det möjligt att beskriva Bennett pinch, Jeans- kriteriet (för gravitationsinstabilitet, i en och två dimensioner), kraftfria magnetfält , gravitationsbalanserade magnetiska tryck, och kontinuerliga övergångar mellan dessa tillstånd.
Referenser inom kultur
En fiktiv nypgenererande enhet användes i Ocean's Eleven , där den användes för att störa Las Vegas elnät precis tillräckligt länge för att karaktärerna skulle börja sitt rån.
Se även
- Elektromagnetisk formning
- Explosivt pumpad flödeskompressionsgenerator
- Fusionskraft
- Lista över plasmafysikartiklar
- Madison Symmetric Torus (omvänd fältnypa)
externa länkar
- Exempel på elektromagnetiskt krympta mynt och krossade burkar
- Teorin om elektromagnetisk mynts krympning
- Den kända historien om "Quarter Shrinking"
- Kan krossa info med hjälp av bland annat elektromagnetism
- MAGPIE-projektet vid Imperial College London används för att studera wire array Z-pinch implosioner.
























![{\displaystyle {\begin{aligned}{\frac {1}{4}}{\frac {\partial ^{2}J_{0}}{\partial t^{2}}}={}&W_{\perp {\text{kin}}}+\Delta W_{E_{z}}+\Delta W_{B_{z}}+\Delta W_{k}-{\frac {\mu _{0}}{8\pi }}I^{2}(a)\\[8pt]&{}-{\frac {1}{2}}G{\overline {m}}^{2}N^{2}(a)+{\frac {1}{2}}\pi a^{2}\epsilon _{0}\left(E_{r}^{2}(a)-E_{\phi }^{2}(a)\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71e972f92a0d232a7244df3fa2ed04d57711196f)
