Partiell luxation

För den syntaktiska operationen, se Dislokation (syntax) . För den medicinska termen, se Ledluxation .

Inom materialvetenskap är en partiell dislokation en nedbruten form av dislokation som uppstår i ett kristallint material. En förlängd luxation är en luxation som har dissocierat till ett par partiella luxationer. Vektorsumman för Burgers-vektorerna för de partiella dislokationerna är Burgers-vektorn för den utökade dislokationen.

Reaktionsgynnsamhet

En dislokation kommer att sönderdelas till partiella dislokationer om energitillståndet för summan av partialerna är mindre än energitillståndet för den ursprungliga dislokationen. Detta sammanfattas av Franks energikriterium :

${\begin{aligned}|{\boldsymbol {b_{1}}}|^{2}>&|{\boldsymbol {b_{2}}}|^{2 }+|{\boldsymbol {b_{3}}}|^{2}{\text{ (gynnsam, kommer att bryta ner)}}\\|{\boldsymbol {b_{1}}}|^{2}<& |{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2}{\text{ (inte gynnsamt, bryts inte ned)}}\\| {\boldsymbol {b_{1}}}|^{2}=&|{\boldsymbol {b_{2}}}|^{2}+|{\boldsymbol {b_{3}}}|^{2} {\text{ (förblir i ursprungligt tillstånd)}}\end{aligned}}$

Shockley partiella dislokationer

Shockley partiella dislokationer hänvisar i allmänhet till ett par dislokationer som kan leda till närvaron av staplingsfel . Detta par av partiella dislokationer kan möjliggöra dislokationsrörelse genom att tillåta en alternativ väg för atomrörelse.

${\begin{aligned}{\boldsymbol {b_{1}}}\högerpil {\boldsymbol {b_{2}}}+{\boldsymbol {b_{3}}} \end{aligned}}$

I FCC-system är ett exempel på Shockley-nedbrytning:

${\begin{aligned}{\frac {a}{2}}[10{\overline { 1}}]\rightarrow {\frac {a}{6}}[2{\overline {1}}{\overline {1}}]+{\frac {a}{6}}[11{\overline { 2}}]\end{aligned}}$

Vilket är energetiskt fördelaktigt:

${\begin{aligned}|{\frac {a}{2}}{\sqrt {1^{2}+0^{2}+(- 1)^{2}}}|^{2}>&|{\frac {a}{6}}{\sqrt {2^{2}+(-1)^{2}+(-1)^ {2}}}|^{2}+|{\frac {a}{6}}{\sqrt {1^{2}+1^{2}+(-2)^{2}}}|^ {2}\\{\frac {a^{2}}{2}}>&{\frac {a^{2}}{6}}+{\frac {a^{2}}{6}} \end{aligned}}$

Komponenterna i Shockley-partialerna måste läggas till den ursprungliga vektorn som bryts ned:

${\begin{aligned}{\frac {a}{2}}(1)=&{\frac {a}{6}}(2)+{\frac {a}{6 }}(1)\\{\frac {a}{2}}(0)=&{\frac {a}{6}}(-1)+{\frac {a}{6}}(1) \\{\frac {a}{2}}(-1)=&{\frac {a}{6}}(-1)+{\frac {a}{6}}(-2)\end{ Justerat}}$

Frank partiella luxationer

Frank partiella dislokationer är fastsittande (orörliga), men kan röra sig genom diffusion av atomer. I FCC-system ges Frank-partialer av:

${\begin{aligned}{\boldsymbol {b}}_{\text{frank}}=&{\frac {a}{3}}[{\text {1 1 1}}]\end{aligned}}$

Thompson tetraeder

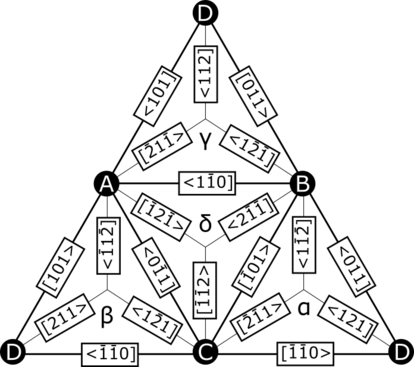
För FCC-kristaller är Thompson-tetraeder eller Thompson-notation en uppfunnen notation för att lättare beskriva partiella dislokationer. I en given enhetscell markerar du punkt A vid utgångspunkten, punkt B vid a/2 [110], punkt C vid a/2[011] och punkt D vid a/2[101] - dessa punkter bildar hörnen av en tetraeder. Markera sedan mitten av de motsatta ytorna för varje punkt som α, β, γ respektive δ. Med detta är den geometriska representationen av en Thompson-tetraeder komplett.

Thompson tetraeder dras in i en FCC-kristall och roteras sedan för att lättare se ansikten och hörn.

Vilken kombination av romerska bokstäver som helst beskriver en medlem av {111} glidplanen i en FCC-kristall. En vektor gjord av två romerska bokstäver beskriver Burgers vektor för en perfekt dislokation. Om vektorn är gjord av en romersk bokstav och en grekisk bokstav, så är det en Frank-partial om bokstäverna är motsvarande (Aα,Bβ,...) eller en Shockley-partial annars (Aβ, Aγ,...). Vektorer gjorda av två grekiska bokstäver beskriver trappstångsförskjutningar. Med hjälp av Thompson-notation kan Burgers-vektorer läggas till för att beskriva andra dislokationer och mekanismer. Till exempel kan två Shockley partiella dislokationer läggas till för att bilda en perfekt dislokation: Aβ + βC = AC. Det är nödvändigt att de inre bokstäverna i en given operation matchar, men många kan läggas till i sekvens för att beskriva mer komplexa mekanismer.

Det är användbart att sammanfatta denna information med en ovikt Thompson-tetraeder.

Ovikta Thompson-tetraedrar innehåller information för att snabbt se Burgers-vektorers relativa riktningar i en FCC-struktur.

Lomer–Cottrell lås

Huvudartikel: Lomer–Cottrell-korsningen

Lomer-Cottrell-dislokationen bildas via en mer komplex dislokationsreaktion. Tänk till exempel på två förlängda dislokationer: DB = Dγ + γB och BC = Bδ + δC. När de möts är det mer energimässigt fördelaktigt att bilda en enda dislokation, DC = DB + BC = Dγ + γB + Bδ + δC = Dγ + γδ + δC. De bakre partierna av varje förlängd dislokation bildar nu en trappstångspartial. Denna struktur leder till minskad rörlighet för dislokationerna eftersom kärnstrukturen är icke-plan (vilket betyder att den inte korsar längs tetraederns yta). Denna minskning av rörligheten förvandlar Lomer-Cottrell-dislokationen till ett hinder för andra dislokationer, vilket stärker materialet.

Mekaniska konsekvenser

Vid bildande av staplingsfel når de partiella dislokationerna en jämvikt när den repulsiva energin mellan partiella dislokationer matchar den attraktiva energin hos staplingsfelet. Detta innebär att material med högre staplingsfelenergi, dvs de med hög skjuvmodul och stora Burgers-vektorer, kommer att ha mindre avstånd mellan partiella dislokationer. Omvänt kommer lågstaplingsfelenergimaterial att ha stora avstånd mellan partiella dislokationer.

Partiella dislokationer rör sig fritt, men för att korshalka till ett annat plan måste de först dra ihop sig innan de glider på ett annat plan.

För att korsa glidning måste båda partiella dislokationerna byta glidplan. Den vanliga Friedel-Escaig-mekanismen kräver att de partiella dislokationerna rekombineras vid en punkt innan de korsar glider in på ett annat glidplan. Att sammanföra delarna innebär att man applicerar tillräcklig skjuvspänning för att minska avståndet mellan dem, så partiella dislokationer med låga staplingsförkastningsenergier blir i sig svårare att sammanföra och därmed svårare att korsglida. Omvänt kommer högstapling av felenergimaterial att vara lättare att korshalka.

Ju lättare en dislokation kan korsa glidning, desto friare kan dislokationen röra sig runt hinder – detta försvårar arbetshärdningen. Således kommer material som tillåter lätt korsglidning (hög staplingsfelenergi) att se mindre arbetshärdning och förstärkning från metoder som solid-lösningsförstärkning.