Orsaksdiagram

Inom statistik, ekonometri, epidemiologi, genetik och relaterade discipliner är kausala grafer (även kända som path diagrams , causal Bayesian networks eller DAGs ) probabilistiska grafiska modeller som används för att koda antaganden om datagenereringsprocessen.

Kausala grafer kan användas för kommunikation och för slutledning. De är komplementära till andra former av kausala resonemang, till exempel med kausal likhetsnotation. Som kommunikationsenheter ger graferna en formell och transparent representation av de orsaksantaganden som forskare kan vilja förmedla och försvara. Som inferensverktyg gör graferna det möjligt för forskare att uppskatta effektstorlekar från icke-experimentella data, härleda testbara implikationer av de kodade antagandena, testa för extern validitet och hantera saknade data och urvalsbias.

Kausala grafer användes först av genetikern Sewall Wright under rubriken "path diagrams". De antogs senare av samhällsvetare och, i mindre utsträckning, av ekonomer. Dessa modeller var initialt begränsade till linjära ekvationer med fasta parametrar. Modern utveckling har utvidgat grafiska modeller till icke-parametrisk analys, och därmed uppnått en generalitet och flexibilitet som har förändrat kausalanalys inom datavetenskap, epidemiologi och samhällsvetenskap.

Konstruktion och terminologi

Den kausala grafen kan ritas på följande sätt. Varje variabel i modellen har en motsvarande vertex eller nod och en pil dras från en variabel X till en variabel Y närhelst Y bedöms svara på förändringar i X när alla andra variabler hålls konstanta. Variabler kopplade till Y genom direkta pilar kallas föräldrar till Y , eller "direkta orsaker till Y ," och betecknas med Pa(Y) .

Orsaksmodeller inkluderar ofta "feltermer" eller "utelämnade faktorer" som representerar alla omätade faktorer som påverkar en variabel Y när Pa(Y) hålls konstant. I de flesta fall exkluderas feltermer från grafen. Men om grafförfattaren misstänker att feltermerna för två variabler är beroende (t.ex. de två variablerna har en oobserverad eller latent gemensam orsak) så dras en dubbelriktad båge mellan dem. Således beaktas närvaron av latenta variabler genom korrelationerna de inducerar mellan feltermerna, som representeras av dubbelriktade bågar.

Grundläggande verktyg

Ett grundläggande verktyg i grafisk analys är d-separation , som gör det möjligt för forskare att genom inspektion avgöra om orsaksstrukturen innebär att två uppsättningar av variabler är oberoende givet en tredje uppsättning. I rekursiva modeller utan korrelerade feltermer (ibland kallade Markovian ), representerar dessa villkorade oberoende modellens alla testbara implikationer.

Exempel

Anta att vi vill uppskatta effekten av att gå på ett elithögskola på framtida inkomster. Att helt enkelt sänka inkomsterna på collegebetyg ger inte en opartisk uppskattning av måleffekten eftersom elithögskolor är mycket selektiva och studenter som går på dem kommer sannolikt att ha kvalifikationer för höginkomstarbeten innan de går i skolan. Om man antar att orsakssambanden är linjära kan denna bakgrundskunskap uttryckas i följande för strukturekvationsmodeller ( SEM).

Modell 1

${\begin{aligned }Q_{1}&=U_{1}\\C&=a\cdot Q_{1}+U_{2}\\Q_{2}&=c\cdot C+d\cdot Q_{1}+U_{ 3}\\S&=b\cdot C+e\cdot Q_{2}+U_{4},\end{aligned}}$

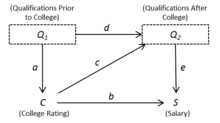
där $Q_{1}$ representerar individens kvalifikationer före college, $Q_{2}$ representerar kvalifikationer efter college, $C$ innehåller attribut som representerar kvaliteten på college som gått, och $S$ individens lön.

Figur 1: Oidentifierad modell med latenta variabler ( $Q_{1}$ och $Q_{2}$ ) visas explicit

Figur 2: Oidentifierad modell med latenta variabler sammanfattade

Figur 1 är en kausal graf som representerar denna modellspecifikation. Varje variabel i modellen har en motsvarande nod eller vertex i grafen. Dessutom, för varje ekvation, dras pilar från de oberoende variablerna till de beroende variablerna. Dessa pilar reflekterar riktningen för orsakssambandet. I vissa fall kan vi märka pilen med dess motsvarande strukturella koefficient som i figur 1.

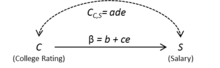
Om $Q_{1}$ och $Q_{2}$ är oobserverade eller latenta variabler kan deras inflytande på $C$ och $S$ tillskrivas deras feltermer . Genom att ta bort dem får vi följande modellspecifikation:

Modell 2

${\begin{aligned}C&=U_{C}\\S&=\beta C+U_{S}\end{aligned}}$

Bakgrundsinformationen som specificeras av modell 1 antyder att feltermen för $S$ , $U_{S}$ , är korrelerad med C :s felterm, $U_{C}$ . Som ett resultat lägger vi till en dubbelriktad båge mellan S och C , som i figur 2.

Figur 3: Identifierad modell med latenta variabler ( $Q_{1}$ och $Q_{2}$ ) visas explicit

Figur 4: Identifierad modell med latenta variabler sammanfattade

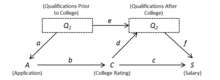
Eftersom $U_{S}$ är korrelerad med $U_{C}$ och därför ${\displaystyle C} ,$ är C $\displaystyle C}$ endogen och $\beta$ identifieras inte i modell 2. Men om vi inkluderar styrkan av en individs högskoleansökan, ${\displaystyle A} ,$ som visas i figur 3, får vi följande modell:

Modell 3

${\begin{aligned}Q_{1}&=U_{1}\\A&=a\cdot Q_{1}+U_{2}\\C&=b\cdot A+U_{3}\\ Q_{2}&=e\cdot Q_{1}+d\cdot C+U_{4}\\S&=c\cdot C+f\cdot Q_{2}+U_{5},\end{aligned} }$

Genom att ta bort de latenta variablerna från modellspecifikationen får vi:

Modell 4

${\begin{aligned}A&=a\cdot Q_{1}+U_{A}\ \C&=b\cdot A+U_{C}\\S&=\beta \cdot C+U_{S},\end{aligned}}$

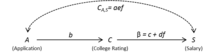
med $U_{A}$ korrelerad med $U_{S}$ .

Nu är $\beta$ identifierad och kan uppskattas med hjälp av regressionen av $S$ på $C$ och $A$ . Detta kan verifieras genom att använda endörrskriteriet , ett nödvändigt och tillräckligt grafiskt villkor för identifiering av en strukturell koefficient, som $\beta$ , med hjälp av regression.