Multitaper

Jämförelse av periodogram (svart) och multitaper-uppskattning (röd) av en lokal fältpotentialmätning för enstaka försök. Denna uppskattning använde 9 tapers.

Inom signalbehandling är multitaper en teknik för uppskattning av spektral densitet utvecklad av David J. Thomson . Den kan uppskatta effektspektrumet S _X för en stationär ergodisk ändlig varians slumpmässig process X , givet en ändlig sammanhängande realisering av X som data.

Motivering

Multitapermetoden övervinner några av begränsningarna med icke-parametrisk Fourier-analys . När man tillämpar Fouriertransformen för att extrahera spektral information från en signal, antar vi att varje Fourierkoefficient är en tillförlitlig representation av amplituden och den relativa fasen för motsvarande komponentfrekvens. Detta antagande är dock inte allmänt giltigt för empiriska data. Till exempel representerar ett enda försök endast en bullrig realisering av den underliggande processen av intresse. En jämförbar situation uppstår i statistiken vid skattning av mått på central tendens , dvs. det är dålig praxis att uppskatta kvaliteter hos en population med hjälp av individer eller mycket små urval. På samma sätt ger ett enda prov av en process inte nödvändigtvis en tillförlitlig uppskattning av dess spektrala egenskaper. Dessutom är den naiva effektspektrala tätheten som erhålls från signalens råa Fourier-transform en partisk uppskattning av det verkliga spektrala innehållet.

Dessa problem övervinns ofta genom att man tar ett medelvärde över många realiseringar av samma händelse efter att man tillämpat en avsmalning på varje försök. Denna metod är dock opålitlig med små datamängder och oönskad när man inte vill dämpa signalkomponenter som varierar mellan försök. Dessutom, även när många försök är tillgängliga, är det icke-avsmalnande periodogrammet generellt förspänt (med undantag för vitt brus) och förspänningen beror på längden av varje realisering, inte antalet registrerade realiseringar. Användning av en enda avsmalning minskar bias men till bekostnad av ökad estimatorvarians på grund av dämpning av aktivitet i början och slutet av varje registrerat segment av signalen. Multitapermetoden undanröjer delvis dessa problem genom att erhålla flera oberoende uppskattningar från samma urval. Varje dataavsmalning multipliceras elementvis med signalen för att tillhandahålla ett fönsterförsök från vilket man uppskattar effekten vid varje komponentfrekvens. Eftersom varje avsmalning är parvis ortogonal mot alla andra avsmalningar, är fönsterfunktionerna okorrelerade med varandra. Det slutliga spektrumet erhålls genom att medelvärdesbilda över alla de avsmalnande spektra och sålunda återvinna en del av informationen som går förlorad på grund av partiell dämpning av signalen som resulterar från applicering av individuella avsmalningar. Den här metoden är särskilt användbar när ett litet antal försök är tillgängligt eftersom den minskar estimatorvariansen utöver vad som är möjligt med metoder med enkel taper. Dessutom, även när många försök är tillgängliga, är multitaper-metoden användbar eftersom den tillåter mer rigorös kontroll av avvägningen mellan bias och varians än vad som är möjligt i fallet med enkel taper. Thomson valde Slepian eller diskreta prolate sfäroidala sekvenser som avsmalnande eftersom dessa vektorer är ömsesidigt ortogonala och besitter önskvärda spektrala koncentrationsegenskaper (se avsnittet om Slepian sekvenser). I praktiken används ofta ett vägt medelvärde för att kompensera för ökad energiförlust vid högre ordnings avsmalningar.

Formulering

Betrakta en p-dimensionell nollmedelvärde för stationär stokastisk process

$\mathbf {X} (t)={\lbrack X(1,t ),X(2,t),\dots ,X(p,t)\rbrack }^{T}$

Här betecknar T matristranspositionen. Inom neurofysiologi till exempel hänvisar p till det totala antalet kanaler och därför kan $\mathbf {X} (t)$ representera samtidig mätning av elektrisk aktivitet för dessa p- kanaler. Låt samplingsintervallet mellan observationer vara $\Delta t$ , så att Nyquist-frekvensen är $f_{N}=1/(2\Delta t)$ .

Multitaper spektral estimatorn använder flera olika data tapers som är ortogonala mot varandra. Multitaper-korsspektrala estimatorn mellan kanal l och m är medelvärdet av K direkta tvärspektrala estimatorer mellan samma par av kanaler ( l och m ) och tar därför formen

${\hat {S}}^{lm}(f)={\frac {1}{K}}\summa _{k=0}^{K-1}{\hat {S}}_ {k}^{lm}(f).$

Här, ${\hat {S}}_{k}^{lm}(f)$ (för $0\leq k\leq K -1$ ) är den k: ^te direkta tvärspektrala estimatorn mellan kanal l och m och ges av

${\hat {S}}_{k}^{lm}( f)={\frac {1}{N\Delta t}}{\lbrack J_{k}^{l}(f)\rbrack }^{*}{\lbrack J_{k}^{m}(f )\rbrack },$

var

$J_{k}^{l}(f)=\sum _{t=1}^{N}h_{t,k}X(l,t)e^{-i2\pi ft\Delta t }.$

De tre ledande Slepian-sekvenserna för T=1000 och 2WT=6. Observera att varje sekvens av högre ordning har en extra nollkorsning.

De slepiska sekvenserna

Sekvensen $\lbrace h_{t,k}\rbrace$ är dataavsmalningen för den k: ^te direkta tvärspektrala estimatorn ${\hat { S}}_{k}^{lm}(f)$ och väljs enligt följande:

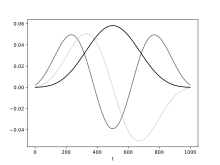
Vi väljer en uppsättning K ortogonala datakonar så att var och en ger ett bra skydd mot läckage. Dessa ges av Slepian-sekvenserna, efter David Slepian (även känd i litteraturen som diskreta prolate sfäroidala sekvenser eller DPSS för kort) med parametern W och order k = 0 till K − 1. Den maximala ordningen K väljs att vara mindre än Shannon nummer $2NW\Delta t$ . Kvantiteten 2 W definierar upplösningsbandbredden för spektralkoncentrationsproblemet och W $\displaystyle W\in (0,f_{N})}$ . När l = m får vi multitaper-estimatorn för autospektrumet för den l: ^te kanalen. På senare år föreslogs en ordbok baserad på modulerad DPSS som ett överkomplett alternativ till DPSS.

Se även Fönsterfunktion:DPSS eller Slepian-fönster

Ansökningar

Denna teknik används för närvarande i Chronux spektralanalysverktyg . En omfattande behandling om tillämpningen av denna metod för att analysera multi-trial, multi-channel data genererad i neurovetenskapliga experiment, biomedicinsk ingenjörskonst och andra kan hittas här . Inte begränsat till tidsserier, multitapermetoden kan omformuleras för spektral uppskattning av sfären med hjälp av Slepian-funktioner konstruerade från sfäriska övertoner för tillämpningar inom geofysik och kosmologi bland annat.

Se även

• Periodogram

•   Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Avsnitt 13.4.3. Multitaper Methods and Slepian Functions" , Numeriska recept: The Art of Scientific Computing (3:e upplagan), New York: Cambridge University Press, ISBN 978-0-521-88068- 8

externa länkar

• [1] C++/Octave-bibliotek för multitapermetoden, inklusive adaptiv viktning (värd på GitHub)
• [2] Dokumentation om multitapermetoden från implementeringen av SSA-MTM Toolkit
• [3] Fortran 90-bibliotek med ytterligare multivariatapplikationer
• [4] Python-modul
• [5] R (programmeringsspråk) multitaper-paket
• [6] S-Plus- skript för att generera Slepian-sekvenser (dpss)