Modulär nedbrytning

I grafteorin är den modulära nedbrytningen en nedbrytning av en graf i delmängder av hörn som kallas moduler. En modul är en generalisering av en sammankopplad komponent i en graf. Till skillnad från anslutna komponenter kan dock en modul vara en riktig delmängd av en annan. Moduler leder därför till en rekursiv (hierarkisk) nedbrytning av grafen, istället för bara en partition .

Det finns varianter av modulär nedbrytning för oriktade grafer och riktade grafer . För varje oriktad graf är denna nedbrytning unik.

Denna uppfattning kan generaliseras till andra strukturer (till exempel riktade grafer) och är användbar för att designa effektiva algoritmer för igenkänning av vissa grafklasser, för att hitta transitiva orienteringar av jämförbarhetsgrafer, för optimeringsproblem på grafer och för grafritning .

Moduler

Eftersom begreppet moduler har återupptäckts inom många områden har moduler också kallats autonoma uppsättningar , homogena uppsättningar , stabila uppsättningar , klumpar , kommittéer , externt relaterade uppsättningar , intervaller , oförenklade subnätverk och partitiva uppsättningar ( Brandstädt, Le & Spinrad 1999 ) . Den kanske tidigaste hänvisningen till dem, och den första beskrivningen av modulära kvoter och den grafnedbrytning de ger upphov till dök upp i ( Gallai 1967).

En modul av en graf är en generalisering av en ansluten komponent . En ansluten komponent har egenskapen att den är en uppsättning $X$ av hörn så att varje medlem av $X$ är en icke-granne till varje vertex inte i $X$ . (Det är en förening av anslutna komponenter om och endast om den har denna egenskap.) Mer generellt $X$ en modul om, för varje vertex $v\not \in X$ , antingen varje medlem av $X$ är en icke-granne till $v$ eller varje medlem av $X$ är en granne till $v$ .

På motsvarande sätt är $X$ en modul om alla medlemmar av $X$ har samma uppsättning grannar bland hörn som inte finns i $X$ .

Till skillnad från de anslutna komponenterna är modulerna i en graf desamma som modulerna i dess komplement , och moduler kan "kapslas": en modul kan vara en riktig delmängd av en annan. Observera att uppsättningen $V$ av hörn i en graf är en modul, liksom dess enelementsdelmängder och den tomma uppsättningen; dessa kallas triviala moduler . En graf kan ha andra moduler eller inte. En graf kallas primtal om alla dess moduler är triviala.

Trots dessa skillnader bevarar moduler en önskvärd egenskap hos anslutna komponenter, vilket är att många egenskaper hos subgrafen $G[X]$ inducerade av en ansluten komponent $X$ är oberoende av resten av grafen. Ett liknande fenomen gäller även subgraferna som induceras av moduler.

Modulerna i en graf är därför av stort algoritmiskt intresse. En uppsättning kapslade moduler, varav den modulära uppdelningen är ett exempel, kan användas för att vägleda den rekursiva lösningen av många kombinatoriska problem på grafer, såsom att känna igen och transitivt orientera jämförbarhetsgrafer , känna igen och hitta permutationsrepresentationer av permutationsgrafer , känna igen om en graf är en kograf och att hitta ett intyg på svaret på frågan, känna igen intervallgrafer och hitta intervallrepresentationer för dem, definiera avståndsärftliga grafer (Spinrad, 2003) och för grafritning (Papadopoulos, 2006). De spelar en viktig roll i Lovász berömda bevis på den perfekta grafsatsen (Golumbic, 1980).

För att känna igen avståndsärftliga grafer och cirkelgrafer är en ytterligare generalisering av modulär nedbrytning, som kallas delad uppdelning , särskilt användbar (Spinrad, 2003).

För att undvika risken för oklarheter i definitionerna ovan, ger vi följande formella definitioner av moduler. $G=(V,E)$ . $M\subseteq V$ är en modul av $G$ om:

hörnen för $M$ kan inte särskiljas av någon vertex i $V\backslash M$ , dvs $\forall u, v\in M,\forall x\in V\backslash M$ , antingen $x$ ligger intill både $u$ och $v$ eller $x$ är varken intill till $u$ eller till $v$ .
hörnen på $M$ har samma uppsättning av yttre grannar, dvs $\forall u,v\in M ,N(u)\setminus M=N(v)\setminus M$ .

$\emptyset$ , $V$ och alla singlar $\{v\}$ för $v\in V$ är moduler och kallas triviala moduler . En graf är primtal om alla dess moduler är triviala. Anslutna komponenter i en graf $G$ eller dess komplementgraf är också moduler av $G$ .

$M$ är en stark modul av en graf $G$ om den inte överlappar någon annan modul i $G$ : $\forall M'$ modul av $G$ , antingen $M\cap M'=\emptyset$ eller $M\subseteq M'$ eller $M'\subseteq M$ .

Modulära kvoter och faktorer

Om $X$ och $Y$ är disjunkta moduler, är det lätt att se att antingen varje medlem av $X$ är granne till varje element i $Y$ , eller ingen medlem av $X$ är intill någon medlem av $Y$ . Således är förhållandet mellan två disjunkta moduler antingen intilliggande eller icke-angränsande . Inget förhållande mellan dessa två ytterligheter kan existera.

På grund av detta är modulära partitioner av $V$ där varje partitionsklass är en modul av särskilt intresse. Antag att $P$ är en modulär partition. Eftersom partitionsklasserna är osammanhängande, utgör deras angränsningar en ny graf, en kvotgraf $G/P$ , vars hörn är medlemmarna av $P$ . Det vill säga, varje hörn av $G/P$ är en modul av G, och närliggande till dessa moduler är kanterna på $G/P$ .

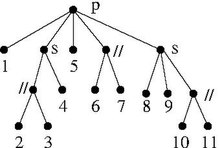
I figuren nedan är hörn 1, hörn 2 till 4, hörn 5, hörn 6 och 7 och hörn 8 till 11 en modulär partition. I det övre högra diagrammet visar kanterna mellan dessa uppsättningar kvoten som ges av denna partition, medan kanterna internt i uppsättningarna visar motsvarande faktorer.

Partitionerna $\{V\}$ och $\{\{x\}|x\in V\}$ är de triviala modulära partitionerna . $G/\{V\}$ är bara grafen med en vertex, medan $G/\{\{x\}|x\in V\}=G$ . Antag att $X$ är en icke-trivial modul. Då $X$ och enelementsundermängderna av $V\backslash X$ en icke-trivial modulär partition av $V$ . Sålunda innebär förekomsten av icke -triviala moduler existensen av icke-triviala modulära partitioner. I allmänhet kan många eller alla medlemmar av $P$ vara icke-triviala moduler.

Om $P$ är en icke-trivial modulär partition, så är $G/P$ en kompakt representation av alla kanter som har ändpunkter i olika partitionsklasser av $P$ . För varje partitionsklass $X$ i $P$ kallas subgrafen $G[X]$ inducerad av ${\displaystyle X} en$ faktor och ger en representation av alla kanter med båda ändpunkterna i $X$ . Därför kan kanterna på $G$ rekonstrueras med endast kvotgrafen $G/P$ och dess faktorer. Termen primtalsgraf kommer från det faktum att en primtalsgraf bara har triviala kvoter och faktorer.

När $G[X]$ är en faktor av en modulär kvot $G/P$ , är det möjligt att $G[X]$ kan vara rekursivt uppdelas i faktorer och kvoter. Varje nivå av rekursionen ger upphov till en kvot. Som basfall har grafen bara en vertex. Sammantaget $G$ rekonstrueras induktivt genom att rekonstruera faktorerna nerifrån och upp, invertera stegen i nedbrytningen genom att kombinera faktorer med kvoten på varje nivå.

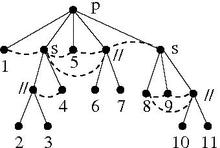
I figuren nedan representeras en sådan rekursiv sönderdelning av ett träd som visar ett sätt att rekursivt bryta ned faktorer för en initial modulär partition till mindre modulära partitioner.

Ett sätt att rekursivt dekomponera en graf i faktorer och kvoter kanske inte är unik. (Till exempel är alla delmängder av hörnen i en komplett graf moduler, vilket betyder att det finns många olika sätt att bryta ner det rekursivt.) Vissa sätt kan vara mer användbara än andra.

Den modulära nedbrytningen

Lyckligtvis finns det en sådan rekursiv sönderdelning av en graf som implicit representerar alla sätt att bryta ner den; detta är den modulära nedbrytningen. Det är i sig ett sätt att dekomponera en graf rekursivt i kvoter, men det subsumerar alla andra. Nedbrytningen som avbildas i figuren nedan är denna speciella nedbrytning för den givna grafen.

En graf, dess kvot där "påsar" med hörn i grafen motsvarar barnen till roten av det modulära nedbrytningsträdet, och dess fullständiga modulära nedbrytningsträd: serienoder är märkta "s", parallella noder "//" och primtal noder "p".

Följande är en viktig observation för att förstå den modulära nedbrytningen:

Om $X$ är en modul av $G$ och $Y$ är en delmängd av $X$ , då är $Y$ en modul av $G$ , om och endast om det är en modul av $G[X]$ .

I (Gallai, 1967) definierade Gallai den modulära nedbrytningen rekursivt på en graf med vertexuppsättningen $V$ , enligt följande:

Som basfall, om $G$ bara har en vertex, är dess modulära nedbrytning en enda trädnod.
Gallai visade att om $G$ är ansluten och dess komplement så är de maximala modulerna som är korrekta delmängder av $V$ en partition av $V$ . De är därför en modulär partition. Den kvot som de definierar är prime. Trädets rot är märkt som en primnod , och dessa moduler är tilldelade som barn till $V$ . Eftersom de är maximala, är varje modul som hittills inte har representerats i ett underordnat $X$ till $V$ . För varje underordnad $X$ av ${\displaystyle V},$ ersätter $X$ med det modulära nedbrytningsträdet för $G[X]$ en representation av alla moduler i $G$ , av nyckelobservationen ovan.
Om $G$ kopplas bort, kopplas dess komplement. Varje förening av anslutna komponenter är en modul av $G$ . Alla andra moduler är delmängder av en enda ansluten komponent. Detta representerar alla moduler, förutom delmängder av anslutna komponenter. För varje komponent $X$ , ersätter $X$ med det modulära nedbrytningsträdet för $G[X]$ ger en representation av alla moduler i $G$ , med nyckelobservationen ovan. Trädets rot är märkt som en parallell nod, och den är fäst i stället för $X$ som ett barn till roten. Den kvot som definieras av barnen är komplementet till en komplett graf.
Om komplementet till $G$ kopplas bort, kopplas ${\displaystyle G} .$ Underträden som är barn till $V$ är definierade på ett sätt som är symmetriskt med fallet där $G$ är frånkopplad, eftersom modulerna i en graf är desamma som modulerna i dess komplement. Trädets rot är märkt som en seriell nod, och kvoten som definieras av barnen är en komplett graf.

Det sista trädet har en-elements uppsättningar av hörn av $G$ som sina blad, på grund av grundfallet. En uppsättning $Y$ av hörn av $G$ är en modul om och endast om det är en nod i trädet eller en förening av barn i en serie eller parallell nod. Detta ger implicit alla modulära partitioner av $V$ . Det är i denna mening som det modulära nedbrytningsträdet "subsumerar" alla andra sätt att rekursivt dekomponera $G$ i kvoter.

Algoritmiska frågor

En datastruktur för att representera det modulära nedbrytningsträdet bör stödja operationen som matar in en nod och returnerar uppsättningen av hörn av $G$ som noden representerar. Ett uppenbart sätt att göra detta på är att tilldela varje nod en lista med $k$ hörn av $G$ som den representerar. Givet en pekare till en nod, skulle denna struktur kunna returnera uppsättningen av hörn av $G$ som den representerar i ${\mathcal {O}}(k)$ tid. Denna datastruktur skulle dock kräva $\Theta (n^{2})$ utrymme i värsta fall.

En

{\mathcal {O}}(n)

representation av den modulära nedbrytningen

Ett ${\mathcal {O}}(n)$ -mellanslagsalternativ som matchar denna prestanda erhålls genom att representera det modulära nedbrytningsträdet med valfri standard ${\mathcal {O} }(n)$ rotad träddatastruktur och märka varje blad med toppunkten på $G$ som det representerar. Mängden som representeras av en intern nod $v$ ges av uppsättningen etiketter för dess lövavkomlingar. Det är välkänt att alla rotade träd med $k$ -löv har högst $k-1$ interna noder. Man kan använda en djup-först-sökning som börjar vid $v$ för att rapportera etiketterna för bladavkomlingar till $v$ i ${\mathcal {O}}(k)$ tid.

Den modulära nedbrytningen, utökad med en kvot på barnen i varje intern nod, ger en fullständig representation av

G

.

Varje nod $X$ är en uppsättning hörn av $G$ och, om $X$ är en intern nod, uppsättningen $P$ av barn till $X$ är en partition av $X$ där varje partitionsklass är en modul. De inducerar därför kvoten $G[X]/P$ i $G[X]$ . Hörnen av denna kvot är elementen i $P$ , så $G[X]/P$ kan representeras genom att installera kanter bland barnen till $X$ . Om $Y$ och $Z$ är två medlemmar av $P$ och $u\in Y$ och $v\in Z$ , då $u$ och $v$ är intilliggande i $G$ om och endast om $Y$ och $Z$ ligger intill i denna kvot. För alla par $\{u,v\}$ av hörn av $G$ bestäms detta av kvoten vid barn till den minst gemensamma förfadern till $\ {u\}$ och $\{v\}$ i det modulära nedbrytningsträdet. Därför ger den modulära nedbrytningen, märkt på detta sätt med kvoter, en fullständig representation av $G$ .

Många kombinatoriska problem kan lösas på $G$ genom att lösa problemet separat på var och en av dessa kvoter. Till exempel $G$ en jämförbarhetsgraf om och endast om var och en av dessa kvoter är en jämförbarhetsgraf (Gallai, 67; Möhring, 85). För att ta reda på om en graf är en jämförbarhetsgraf behöver man därför bara ta reda på om var och en av kvoterna är det. I själva verket, för att hitta en transitiv orientering av en jämförbarhetsgraf, räcker det att transitivt orientera var och en av dessa kvoter av dess modulära upplösning (Gallai, 67; Möhring, 85). Ett liknande fenomen gäller för permutationsgrafer, (McConnell och Spinrad '94), intervallgrafer (Hsu och Ma '99), perfekta grafer och andra grafklasser. Vissa viktiga kombinatoriska optimeringsproblem på grafer kan lösas med en liknande strategi (Möhring, 85).

Kografer är de grafer som bara har parallella eller seriella noder i sitt modulära nedbrytningsträd.

Den första polynomalgoritmen för att beräkna det modulära nedbrytningsträdet för en graf publicerades 1972 (James, Stanton & Cowan 1972) och nu finns linjära algoritmer tillgängliga (McConnell & Spinrad 1999, Tedder et al. 2007, Cournier & Habib 1994).

Generaliseringar

Modulär nedbrytning av riktade grafer kan göras i linjär tid ( Mcconnell & de Montgolfier 2005) .

Med ett litet antal enkla undantag har varje graf med en icke-trivial moduluppdelning också en skev partition ( Reed 2008) .

Brandstädt, Andreas; Le, Van Bang; Spinrad, Jeremy P. (1999). Grafklasser: En undersökning . Föreningen för industriell och tillämpad matematik. doi : 10.1137/1.9780898719796 . ISBN 978-0-89871-432-6 .
Gallai, Tibor (1967). "Transitiv orientierbare Graphen" . Acta Mathematica Academiae Scientiarum Hungaricae . 18 (1–2): 25–66. doi : 10.1007/BF02020961 . MR 0221974 . S2CID 119485995 .
James, Lee O.; Stanton, Ralph G.; Cowan, Donald D. (1972). "Graftupplösning för oriktade grafer". Proc. 3rd Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Florida Atlantic Univ., Boca Raton, Fla., 1972) . Florida Atlantic University . s. 281–290. MR 0351909 .
Golumbic, Martin C. (1980). Algoritmisk grafteori och perfekta grafer . Akademisk press. ISBN 0-444-51530-5 .
Hsu, WL; Ma, T. (1999). "Snabba och enkla algoritmer för att känna igen ackordsjämförbarhetsgrafer och intervallgrafer". SIAM Journal on Computing . 28 (3): 1004–1020. CiteSeerX 10.1.1.104.4647 . doi : 10.1137/S0097539792224814 .
McConnell, Ross M.; de Montgolfier, Fabien (2005). "Modulär sönderdelning i linjär tid av riktade grafer" . Diskret tillämpad matematik . 145 (2): 198–209. doi : 10.1016/j.dam.2004.02.017 .
McConnell, Ross M.; Spinrad, Jeremy P. (1999). "Modulär nedbrytning och transitiv orientering" (PDF) . Diskret matematik . 201 (1–3): 189–241. doi : 10.1016/S0012-365X(98)00319-7 . MR 1687819 .
Möhring, Rolf H. (1985). I. Rival (red.). "Algoritmiska aspekter av jämförbarhetsgrafer och intervallgrafer". Grafer och ordning . D. Reidel: 41–101. doi : 10.1007/978-94-009-5315-4_2 . ISBN 978-94-010-8848-0 .
Möhring, Rolf H. (1985). "Algoritmiska aspekter av substitutionsnedbrytningen i optimering över relationer, uppsättningssystem och booleska funktioner". Annals of Operations Research . 4 : 195-225. doi : 10.1007/BF02022041 . S2CID 119982014 .
Papadopoulos, Charis; Voglis, Constantinos (2005). "Rita grafer med modulär nedbrytning" (PDF) . Proc. 13:e internationella symposium om grafritning (GD'05) . Föreläsningsanteckningar i datavetenskap. Vol. 3843. Springer-Verlag. s. 343–354. doi : 10.1007/11618058_31 . MR 2229205 .
Reed, Bruce (2008). "Skeva partitioner i perfekta grafer" (PDF) . Diskret tillämpad matematik . 156 (7): 1150–1156. doi : 10.1016/j.dam.2007.05.054 . MR 2404228 . Arkiverad från originalet (PDF) 2015-09-19 . Hämtad 2012-08-13 .
Spinrad, Jeremy P. (2003). Effektiva grafrepresentationer . Fields Institutes monografier. American Mathematical Society. ISBN 0-8218-2815-0 .
Tedder, Marc; Corneil, Derek ; Habib, Michel; Paul, Christophe (2008). "Enklare linjär-tidsmodulär nedbrytning via rekursiva faktoriserande permutationer". Proc. 35:e internationella kollokviet om automater, språk och programmering (ICALP 2008) . Föreläsningsanteckningar i datavetenskap. Vol. 5125. Springer-Verlag. s. 634–645. arXiv : 0710.3901 . doi : 10.1007/978-3-540-70575-8_52 .
Zahedi, Emad; Smith, Jason (31 juli 2019). "Modulär nedbrytning av grafer och den avståndsbevarande egenskapen" . Diskret tillämpad matematik . 265 (7): 192–198. arXiv : 1805.09853 . Bibcode : 2018arXiv180509853Z . doi : 10.1016/j.dam.2019.03.019 .

externa länkar