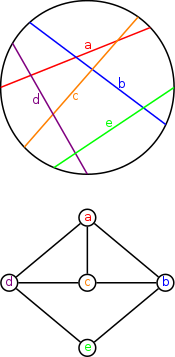
Cirkel graf

För diagrammet, se Cirkeldiagram .

En cirkel med fem ackord och motsvarande cirkeldiagram.

I grafteori är en cirkelgraf skärningsdiagrammet för ett korddiagram . Det vill säga, det är en oriktad graf vars hörn kan associeras med ett ändligt system av ackord i en cirkel så att två hörn ligger intill om och endast om motsvarande ackord korsar varandra.

Algoritmisk komplexitet

Spinrad (1994) ger en O( n ² )-tidsalgoritm som testar om en given n -vertex oriktad graf är en cirkelgraf och, om den är det, konstruerar en uppsättning ackord som representerar den.

Ett antal andra problem som är NP-kompletta på allmänna grafer har polynomiska tidsalgoritmer när de är begränsade till cirkelgrafer. Kloks (1996) visade till exempel att trädbredden för en cirkelgraf kan bestämmas och en optimal trädsönderdelning konstrueras, i O( n ³ ) tid. Dessutom kan en minimifyllning (det vill säga en kordalgraf med så få kanter som möjligt som innehåller den givna cirkelgrafen som en subgraf) hittas i O( n ³ ) tid. Tiskin (2010) har visat att en maximal klick av en cirkelgraf kan hittas i O( n log ² n ) tid, medan Nash & Gregg (2010) har visat att en maximal oberoende uppsättning av en oviktad cirkelgraf kan hittas i O( n min{ d , α }) tid, där d är en parameter i grafen känd som dess densitet, och α är cirkelgrafens oberoende nummer.

Men det finns också problem som förblir NP-kompletta när de begränsas till cirkeldiagram. Dessa inkluderar minsta dominerande uppsättning , minsta anslutna dominerande uppsättning och minsta totala dominerande uppsättning.

Kromatiskt nummer

Ackorden som bildar grafen med 220 vertex 5-kromatisk triangelfri cirkel av Ageev (1996), ritade som ett arrangemang av linjer i det hyperboliska planet .

Det kromatiska numret för en cirkelgraf är det minsta antalet färger som kan användas för att färga dess ackord så att inte två korsande ackord har samma färg. Eftersom det är möjligt att bilda cirkelgrafer där godtyckligt stora uppsättningar av ackord alla korsar varandra, kan det kromatiska numret för en cirkelgraf vara godtyckligt stort, och bestämning av det kromatiska numret för en cirkelgraf är NP-komplett. Det förblir NP-komplett att testa om en cirkelgraf kan färgas med fyra färger. Unger (1992) hävdade att hitta en färgning med tre färger kan göras i polynomtid men hans uppskrivning av detta resultat utelämnar många detaljer.

Flera författare har undersökt problem med att färga begränsade underklasser av cirkeldiagram med få färger. I synnerhet för cirkelgrafer där inga uppsättningar av k eller fler ackord korsar varandra, är det möjligt att färglägga grafen med så få som $7k^{2}$ färger. Ett sätt att påstå detta är att cirkelgraferna är $\chi$ -begränsade . I det speciella fallet när k = 3 (det vill säga för triangelfria cirkelgrafer) är det kromatiska talet högst fem, och detta är snävt: alla triangelfria cirkelgrafer kan färgas med fem färger, och det finns triangel- fria cirkeldiagram som kräver fem färger. Om en cirkelgraf har omkrets (det vill säga den är triangelfri och inte har några cykler med fyra vertex) kan den färgas med högst tre färger. Problemet med att färglägga triangelfria kvadratgrafer är ekvivalent med problemet med att representera kvadratgrafer som isometriska subgrafer av kartesiska produkter av träd ; i denna korrespondens motsvarar antalet färger i färgningen antalet träd i produktrepresentationen.

Ansökningar

Cirkeldiagram uppstår i VLSI fysisk design som en abstrakt representation för ett specialfall för ledningsdirigering , känd som "två-terminal switchbox routing". I det här fallet är ruttområdet en rektangel, alla nät är tvåterminala och terminalerna placeras på rektangelns omkrets. Det är lätt att se att skärningsgrafen för dessa nät är en cirkelgraf. Bland målen med tråddragningssteget är att säkerställa att olika nät förblir elektriskt bortkopplade, och att deras potentiella korsande delar måste läggas ut i olika ledande lager. Därför fångar cirkeldiagram olika aspekter av detta routingproblem.

Färger av cirkelgrafer kan också användas för att hitta bokinbäddningar av godtyckliga grafer: om hörnen på en given graf G är ordnade på en cirkel, där kanterna på G bildar ackord i cirkeln, så är skärningsgrafen för dessa ackord en cirkeldiagram och färger på denna cirkelgraf är likvärdiga med bokinbäddningar som respekterar den givna cirkulära layouten. I denna ekvivalens motsvarar antalet färger i färgläggningen antalet sidor i bokinbäddningen.

Relaterade grafklasser

Ett intervallsystem med fem intervall och motsvarande överlappningsgraf.

En graf är en cirkelgraf om och endast om det är överlappningsgrafen för en uppsättning intervall på en linje. Detta är en graf där hörnen motsvarar intervallen, och två hörn är sammankopplade med en kant om de två intervallen överlappar varandra, utan att det ena innehåller det andra.

Skärningsgrafen för en uppsättning intervall på en linje kallas intervallgrafen .

Stränggrafer , skärningsgraferna för kurvor i planet, inkluderar cirkeldiagram som ett specialfall.

Varje ärftlig avståndsgraf är en cirkelgraf, liksom varje permutationsgraf och varje indifferensgraf . Varje ytterplanär graf är också en cirkelgraf.

Cirkelgraferna är generaliserade av polygon-cirkelgraferna , skärningsdiagram för polygoner som alla är inskrivna i samma cirkel.

Anteckningar

• Ageev, AA (1996), "En triangelfri cirkelgraf med kromatiskt nummer 5", Diskret matematik , 152 (1–3): 295–298, doi : 10.1016/0012-365X(95)00349-2 .
• Ageev, AA (1999), "Every circle graph of girth at least 5 is 3-colourable", Discrete Mathematics , 195 (1–3): 229–233, doi : 10.1016/S0012-365X(98)00192-7 .
•   Bandelt, H.-J.; Chepoi, V.; Eppstein, D. (2010), "Combinatorics and geometry of finite and infinite squaregraphs", SIAM Journal on Discrete Mathematics , 24 (4): 1399–1440, arXiv : 0905.4537 , doi : 10.1167 /3010 S. 8C .
• Černý, Jakub (2007), "Coloring circle graphs", Electronic Notes in Discrete Mathematics , 29 : 357–361, doi : 10.1016/j.endm.2007.07.072 .
•    Davies, James; McCarty, Rose (2021), "Circle graphs are quadratically χ-bounded", Bulletin of the London Mathematical Society , 53 (3): 673–679, arXiv : 1905.11578 , doi : 10.1112/blms.124497 , SMR 2497, S124497 , SMR 124497 , S124497 7723 .
• Garey, MR ; Johnson, DS ; Miller, GL ; Papadimitriou, C. (1980), "The complexity of coloring circular arcs and chords", SIAM Journal on Algebraic and Discrete Methods , 1 (2): 216–227, doi : 10.1137/0601025 .
• Gyárfás, A. (1985), "On the chromatic number of multiple interval graphs and overlap graphs", Discrete Mathematics , 55 (2): 161–166, doi : 10.1016/0012-365X(85)90044-5 . Som citeras av Ageev (1996) .
• Gyárfás, A. ; Lehel, J. (1985), "Täcknings- och färgningsproblem för släktingar av intervall", Diskret matematik , 55 (2): 167–180, doi : 10.1016/0012-365X(85)90045-7 . Som citeras av Ageev (1996) .
• Karapetyan, A. (1984), On perfect arc and chord intersection graphs , Ph.D. avhandling (på ryska), Inst. i matematik, Novosibirsk . Som citeras av Ageev (1996) .
• Keil, J. Mark (1993), "The complexity of domination problems in circle graphs", Discrete Applied Mathematics , 42 (1): 51–63, doi : 10.1016/0166-218X(93)90178-Q .
• Kloks, Ton (1996), "Treewidth of Circle Graphs", Int. J. Funnet. Comput. Sci. , 7 (2): 111–120, doi : 10.1142/S0129054196000099 .
• Kloks, T.; Kratsch, D.; Wong, CK (1998), "Minimum fill-in on circle and circular-arc graphs", Journal of Algorithms , 28 (2): 272–289, doi : 10.1006/jagm.1998.0936 .
•   Kostochka, AV (1988), "Upper bounds on the chromatic number of graphs", Trudy Instituta Mathematiki (på ryska), 10 : 204–226, MR 0945704 . Som citeras av Ageev (1996) .
• Kostochka, AV; Kratochvíl, J. (1997), "Covering and coloring polygon-circle graphs", Discrete Mathematics , 163 (1–3): 299–305, doi : 10.1016/S0012-365X(96)00344-5 .
• Nash, Nicholas; Gregg, David (2010), "An output sensitive algorithm for computing a maximum independent set of a circle graph", Information Processing Letters , 116 (16): 630–634, doi : 10.1016/j.ipl.2010.05.016 , hdl : 10344/2228 .
• Spinrad, Jeremy (1994), "Recognition of circle graphs", Journal of Algorithms , 16 (2): 264–282, doi : 10.1006/jagm.1994.1012 .
• Tiskin, Alexander (2010), "Snabbdistansmultiplikation av enhet-Monge-matriser.", Proceedings of ACM-SIAM SODA 2010 , s. 1287–1296 .
• Unger, Walter (1988), "On the k -colouring of circle-graphs", STACS 88: 5th Annual Symposium on Theoretical Aspects of Computer Science, Bordeaux, Frankrike, 11–13 februari 1988, Proceedings , Lecture Notes in Computer Science vol. 294, Berlin: Springer, s. 61–72, doi : 10.1007/BFb0035832 .
• Unger, Walter (1992), "The complexity of coloring circle graphs", STACS 92: 9th Annual Symposium on Theoretical Aspects of Computer Science, Cachan, Frankrike, 13–15 februari 1992, Proceedings , Lecture Notes in Computer Science, vol. 577, Berlin: Springer, s. 389–400, doi : 10.1007/3-540-55210-3_199 .
• Wessel, W.; Pöschel, R. (1985), "On circle graphs", i Sachs, Horst (red.), Graphs, Hypergraphs and Applications: Proceedings of the Conference on Graph Theory som hölls i Eyba, 1 till 5 oktober 1984, Teubner-Texte zur Mathematik, vol. 73, BG Teubner, s. 207–210 . Som citeras av Unger (1988) .