Membranberäkning
Membrane computing (eller MC ) är ett område inom datavetenskap som försöker upptäcka nya beräkningsmodeller från studiet av biologiska celler , särskilt av cellmembranen . Det är en deluppgift att skapa en cellulär modell .
Membranberäkning handlar om distribuerade och parallella beräkningsmodeller, bearbetning av flera uppsättningar av symbolobjekt på ett lokaliserat sätt. Således tillåter evolutionsreglerna att utvecklande objekt kan kapslas in i fack som definieras av membran. Kommunikationerna mellan fack och med omgivningen spelar en väsentlig roll i processerna. De olika typerna av membransystem är kända som P-system efter Gheorghe Păun som först tänkte ut modellen 1998.
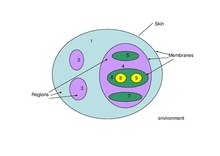
En väsentlig ingrediens i ett P-system är dess membranstruktur, som kan vara ett hierarkiskt arrangemang av membran, som i en cell, eller ett nät av membran (placerade i noderna i en graf), som i en vävnad eller ett neuralt nät. P-system avbildas ofta grafiskt med ritningar.
Intuitionen bakom föreställningen om ett membran är en tredimensionell vesikel från biologin. Men själva konceptet är mer generellt, och ett membran ses som en separator av två regioner. Membranet tillhandahåller selektiv kommunikation mellan de två regionerna. Enligt Gheorghe Păun är separationen av det euklidiska rummet i en ändlig "insida" och en oändlig "utsida". Den selektiva kommunikationen är där datorn kommer in.
Grafiska representationer kan ha många element, beroende på variationen av modellen som studeras. Till exempel kan en regel producera den speciella symbolen δ, i vilket fall membranet som innehåller den löses upp och allt dess innehåll flyttas upp i regionhierarkin.
Mångfalden av förslag från biologi och utbudet av möjligheter att definiera arkitekturen och funktionen hos en membranbaserad multiset-behandlingsenhet är praktiskt taget oändliga. Faktum är att membranberäkningslitteraturen innehåller ett mycket stort antal modeller. Således är MC inte bara en teori relaterad till en specifik modell, det är ett ramverk för att ta fram kompartmentiserade modeller.
Kemikalier modelleras av symboler, alternativt genom strängar av symboler. Området, som definieras av ett membran, kan innehålla andra symboler eller strängar (kollektivt kallade objekt) eller andra membran, så att ett P-system har exakt ett yttre membran, kallat hudmembranet, och ett hierarkiskt förhållande som styr alla dess hinnor under hudhinnan.
Om objekt är symboler, så spelar deras mångfald inom en region betydelse; men multi-set används också i vissa strängmodeller. Regioner har associerade regler som definierar hur objekt produceras, konsumeras, skickas till andra regioner och på annat sätt interagerar med varandra. Den icke-deterministiska maximalt parallella tillämpningen av regler genom hela systemet är en övergång mellan systemtillstånd, och en sekvens av övergångar kallas en beräkning. Särskilda mål kan definieras för att beteckna ett stopptillstånd, vid vilken punkt resultatet av beräkningen skulle vara de objekt som finns i en viss region. Alternativt kan resultatet bestå av föremål som skickas ut från hudmembranet till omgivningen.
Många variantmodeller har studerats, och intresset har fokuserat på att bevisa beräkningsuniversalitet för system med ett litet antal membran, i syfte att lösa NP-kompletta problem såsom Boolean satisfiability (SAT) problem och traveling salesman problem (TSP) . P -systemen kan byta rum- och tidskomplexitet och använder mindre ofta modeller för att förklara naturliga processer i levande celler. Studierna tar fram modeller som åtminstone teoretiskt kan implementeras på hårdvara. Hittills P-systemen nästan alla teoretiska modeller som aldrig har reducerats till praktik, även om ett praktiskt system ges in.