Matematik för trefas elektrisk kraft

En spänningscykel i ett trefassystem, märkt 0 till 360° (2π radianer) längs tidsaxeln. Den plottade linjen representerar variationen av momentan spänning (eller ström) med avseende på tiden. Denna cykel upprepas med en frekvens som beror på kraftsystemet.

Inom elektroteknik har trefasiga elkraftsystem minst tre ledare som bär växelspänningar som är förskjutna i tiden med en tredjedel av perioden. Ett trefassystem kan vara arrangerat i delta (∆) eller stjärna (Y) (även betecknat som wye i vissa områden, eftersom det symboliskt liknar bokstaven "Y"). Ett wye-system tillåter användning av två olika spänningar från alla tre faserna , till exempel ett 230/400 V-system som ger 230 V mellan nollan (mittnavet) och vilken som helst av faserna, och 400 V över alla två faser. Ett deltasystemarrangemang ger bara en spänning, men det har en större redundans eftersom det kan fortsätta att fungera normalt med en av de tre matningslindningarna offline, om än på 57,7 % av den totala kapaciteten. Övertonsströmmen i nollan kan bli mycket stor om olinjära laster ansluts.

Definitioner

I en stjärnkopplad (wye) topologi, med rotationssekvens L1 - L2 - L3, kan de tidsvarierande momentana spänningarna beräknas för varje fas A, C, B respektive genom:

$V_{L1-N}=V_{P}\sin \left(\theta \right)\,\!$

$V_{L2-N}=V_{P}\sin \left(\theta -{\frac {2}{ 3}}\pi \right)=V_{P}\sin \left(\theta +{\frac {4}{3}}\pi \right)$

$V_{L3-N}=V_{P}\sin \left(\theta -{\frac {4}{3}}\pi \right)=V_{P}\sin \left(\theta +{\frac {2}{3}}\pi \right)$

var:

$V_{P}$ är toppspänningen,

$\theta =2\pi ft\,\!$ är fasvinkeln i radianer

$t$ är tid i sekunder

$f$ är frekvensen i cykler per sekund och

spänningarna L1-N, L2-N och L3-N refereras till stjärnanslutningspunkten.

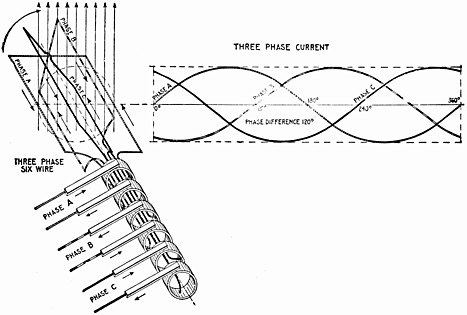
Diagram

Bilderna nedan visar hur ett system med sex ledningar som levererar tre faser från en generator kan ersättas med bara tre. En trefastransformator visas också.

• 

  Elementär sextråds trefasgenerator, där varje fas använder ett separat par överföringsledningar.

• 

  Elementär trefasgenerator med tre trådar, som visar hur faserna endast kan dela tre transmissionstrådar.

• 

  Varje fas i en trefastransformator har sina egna lindningar, med en delad kärna.

Balanserade laster

Generellt, i elektriska kraftsystem, är lasterna fördelade så jämnt som är praktiskt möjligt mellan faserna. Det är vanlig praxis att först diskutera ett balanserat system och sedan beskriva effekterna av obalanserade system som avvikelser från det elementära fallet.

Konstant kraftöverföring

En viktig egenskap hos trefaseffekt är att den momentana effekt som är tillgänglig för en resistiv belastning, $\scriptstyle P\,=\,VI\,=\,{\frac {V^ {2}}{R}}$ , är konstant hela tiden. Verkligen, låt

${\begin{aligned}P_{Li}&={\frac {V_{Li}^{2}}{R} }\\P_{TOT}&=\summa _{i}P_{Li}\end{aligned}}$

För att förenkla matematiken definierar vi en icke-dimensionaliserad potens för mellanliggande beräkningar, $\scriptstyle p\,=\,{\frac {1}{V_{P}^{2 }}}P_{TOT}R$

$p=\sin ^{2}\theta +\sin ^{2 }\left(\theta -{\frac {2}{3}}\pi \right)+\sin ^{2}\left(\theta -{\frac {4}{3}}\pi \right) ={\frac {3}{2}}$

Därför (ersätter tillbaka):

$P_{TOT}={\frac {3V_{P}^{2}}{2R}}.$

Eftersom vi har eliminerat $\theta$ kan vi se att den totala effekten inte varierar med tiden. Detta är viktigt för att hålla stora generatorer och motorer igång smidigt.

Lägg också märke till att med hjälp av rotmedelvärdespänningen ${\displaystyle V={\frac {V_{p}}{\sqrt {2}}}} ,$ uttrycket för $P_{ TOT}$ ovan har följande mer klassiska form:

$P_{TOT}={\frac {3V^{2}}{R}}$ .

Belastningen behöver inte vara resistiv för att uppnå en konstant momentan effekt eftersom, så länge den är balanserad eller lika för alla faser, kan den skrivas som

$Z=|Z|e^{j\varphi }$

så att toppströmmen är

$I_{P}={\frac {V_{P}}{|Z|}}$

för alla faser och de momentana strömmarna är

$I_{L1}=I_{P}\sin \left(\theta -\varphi \right)$

$I_{L2}=I_{P}\sin \left(\theta -{\frac {2}{3}}\pi -\varphi \right)$

$I_{L3}=I_{P}\sin \left(\theta -{\frac {4}{3}}\pi -\varphi \right)$

Nu är de momentana krafterna i faserna

$P_{L1}=V_{L1}I_{L1}=V_{P}I_{ P}\sin \left(\theta \right)\sin \left(\theta -\varphi \right)$

$P_{L2}=V_{L2}I_{L2}=V_{P}I_{P}\sin \left(\theta -{\frac {2} {3}}\pi \right)\sin \left(\theta -{\frac {2}{3}}\pi -\varphi \right)$

$P_{L3}=V_{L3}I_{L3}=V_{P}I_{P}\sin \left (\theta -{\frac {4}{3}}\pi \right)\sin \left(\theta -{\frac {4}{3}}\pi -\varphi \right)$

Använda vinkelsubtraktionsformler :

$P_{L1}={\frac {V_{P}I_{P}}{2}} \left[\cos \left(\varphi \right)-\cos \left(2\theta -\varphi \right)\right]$

$P_{L2}={\frac {V_{P}I_{P}}{2}}\left[\cos \left(\varphi \right)- \cos \left(2\theta -{\frac {4}{3}}\pi -\varphi \right)\right]$

$P_{L3}={\frac {V_{P}I_{P}}{2}}\left[\cos \left(\varphi \right)-\ cos \left(2\theta -{\frac {8}{3}}\pi -\varphi \right)\right]$

som summerar till en total momentan kraft

$P_{TOT}={\frac {V_{P}I_{P}}{2}}\left\{3\cos \varphi -\left[\cos \left(2\theta - \varphi \right)+\cos \left(2\theta -{\frac {4}{3}}\pi -\varphi \right)+\cos \left(2\theta -{\frac {8}{ 3}}\pi -\varphi \right)\right]\right\}$

Eftersom de tre termerna inom hakparenteser är ett trefassystem, summeras de till noll och den totala effekten blir

$P_{TOT}={\frac {3V_{P}I_{P}}{2}}\cos \varphi$

eller

$P_{TOT}={\frac {3V_{P}^{2}}{2|Z|}}\cos \varphi$

visar påståendet ovan.

Återigen, med hjälp av rotmedelvärdespänningen ${\displaystyle V={\frac {V_{p}}{\sqrt {2}}}} ,$ P $\displaystyle P_{TOT}}$ kan skrivs i vanlig form

$P_{TOT}={\frac {3V^{2}}{Z}}\cos \varphi$ .

Ingen nollström

För fallet med lika belastningar på var och en av tre faser flyter ingen nettoström i nollan. Neutralströmmen är den inverterade vektorsumman av linjeströmmarna. Se Kirchhoffs kretslagar .

${\begin{aligned}I_{L1}&={\frac {V_{L1-N}}{R}},\;I_{L2}={\frac {V_{L2-N}}{R}} ,\;I_{L3}={\frac {V_{L3-N}}{R}}\\-I_{N}&=I_{L1}+I_{L2}+I_{L3}\end{aligned }}$

Vi definierar en icke-dimensionaliserad ström, $i={\frac {I_{N}R}{V_{P}}}$ :

${\begin{aligned}i&=\sin \left(\theta \right)+\sin \left(\theta -{\frac {2\pi }{3 }}\right)+\sin \left(\theta +{\frac {2\pi }{3}}\right)\\&=\sin \left(\theta \right)+2\sin \left( \theta \right)\cos \left({\frac {2\pi }{3}}\right)\\&=\sin \left(\theta \right)-\sin \left(\theta \right) \\&=0\end{aligned}}$

Eftersom vi har visat att nollströmmen är noll kan vi se att borttagning av nollkärnan inte har någon effekt på kretsen, förutsatt att systemet är balanserat. Sådana anslutningar används i allmänhet endast när belastningen på de tre faserna är en del av samma utrustning (till exempel en trefasmotor), eftersom omkoppling av laster och små obalanser annars skulle orsaka stora spänningsfluktuationer.

Obalanserade system

I praktiken har system sällan perfekt balanserade belastningar, strömmar, spänningar och impedanser i alla tre faserna. Analysen av obalanserade fall förenklas avsevärt genom användningen av teknikerna för symmetriska komponenter . Ett obalanserat system analyseras som överlagringen av tre balanserade system, vart och ett med positiv, negativ eller noll sekvens av balanserade spänningar.

När vi anger ledningsstorlekar i ett trefassystem behöver vi bara veta storleken på fas- och neutralströmmarna. Neutralströmmen kan bestämmas genom att addera de tre fasströmmarna tillsammans som komplexa tal och sedan omvandla från rektangulära till polära koordinater. Om de trefasiga rotmedelkvadratströmmarna (RMS) är $I_{L1}$ , $I_{L2}$ och $I_{L3}$ , den neutrala RMS-strömmen är:

${ \displaystyle I_{L1}+I_{L2}\cos \left({\frac {2}{3}}\pi \right)+jI_{L2}\sin \left({\frac {2}{3} }\pi \right)+I_{L3}\cos \left({\frac {4}{3}}\pi \right)+jI_{L3}\sin \left({\frac {4}{3} }\pi \right)}$

som löser sig till

$I_{L1}-I_{L2}{\frac {1}{2}} -I_{L3}{\frac {1}{2}}+j{\frac {\sqrt {3}}{2}}\left(I_{L2}-I_{L3}\right)$

Den polära magnituden av detta är kvadratroten av summan av kvadraterna av de reella och imaginära delarna, vilket reducerar till

${\sqrt {I_{L1}^{2} +I_{L2}^{2}+I_{L3}^{2}-I_{L1}I_{L2}-I_{L1}I_{L3}-I_{L2}I_{L3}}}$

Icke-linjära belastningar

Vid linjära belastningar bär nollan endast strömmen på grund av obalans mellan faserna. Enheter som använder likriktare-kondensatorfrontar (såsom switch-mode strömförsörjning för datorer, kontorsutrustning och liknande) introducerar tredje ordningens övertoner. Tredje övertonsströmmar är i fas på var och en av matningsfaserna och kommer därför att läggas samman i nollan, vilket kan göra att nollströmmen i ett wye-system överstiger fasströmmarna.

Roterande magnetfält

Vilket flerfassystem som helst, i kraft av tidsförskjutningen av strömmarna i faserna, gör det möjligt att enkelt generera ett magnetfält som roterar med linjefrekvensen. Ett sådant roterande magnetfält gör flerfasiga induktionsmotorer möjliga. Faktum är att där induktionsmotorer måste köras på enfaseffekt (såsom vanligtvis distribueras i hem), måste motorn innehålla någon mekanism för att producera ett roterande fält, annars kan motorn inte generera något stillastående vridmoment och kommer inte att starta . Fältet som produceras av en enfaslindning kan ge energi till en motor som redan roterar, men utan hjälpmekanismer kommer motorn inte att accelerera från ett stopp.

Ett roterande magnetfält med stadig amplitud kräver att alla tre fasströmmarna är lika stora och exakt förskjutna en tredjedel av en cykel i fas. Obalanserad drift resulterar i oönskade effekter på motorer och generatorer.

Konvertering till andra fassystem

Förutsatt att två spänningsvågformer har åtminstone en viss relativ förskjutning på tidsaxeln, annat än en multipel av en halvcykel, kan vilken annan flerfasig uppsättning spänningar som helst erhållas av en grupp passiva transformatorer . Sådana arrayer kommer att jämnt balansera flerfasbelastningen mellan faserna i källsystemet. Till exempel kan balanserad tvåfaseffekt erhållas från ett trefasnät genom att använda två specialkonstruerade transformatorer, med uttag på 50 % och 86,6 % av primärspänningen. Denna Scott T- anslutning producerar ett äkta tvåfassystem med 90° tidsskillnad mellan faserna. Ett annat exempel är genereringen av system med högre fasordning för stora likriktarsystem , för att producera en jämnare DC- utgång och för att minska de övertonsströmmar i matningen.

När trefas behövs men endast enfas är lättillgängligt från elleverantören, kan en fasomvandlare användas för att generera trefaseffekt från enfasförsörjningen. En motorgenerator används ofta i industriella fabriksapplikationer.

Systemmått

I ett trefassystem krävs minst två givare för att mäta effekt när det inte finns någon neutral, eller tre givare när det finns en neutral. Blondels teorem säger att antalet mätelement som krävs är en mindre än antalet strömförande ledare.

Se även

• Charles Proteus Steinmetz
• Galileo Ferraris
• John Hopkinson
• Mikhail Dolivo-Dobrovolsky
• Nikola Tesla
• Flerfassystem
• Trefas elkraft
• Y-A transformation

•   Stevenson, William D. Jr. (1975). Element i kraftsystemanalys . McGraw-Hill Electrical and Electronic Engineering Series (3:e upplagan). New York: McGraw-Hill. ISBN 0-07-061285-4 .