MLAB
 | |
| Utvecklare | Civilized Software Inc. |
|---|---|
| Initial release | 1985 |
| Skrivet i | C , Assembler , MLAB |
| Operativ system | Cross-platform : Microsoft Windows , Linux och Mac OS X |
| Plattform | IA-32 , x86-64 |
| Typ | Numerisk beräkning |
| Licens | Proprietär kommersiell programvara |
| Hemsida | |
| Paradigm | multi-paradigm : funktionell , imperativ , processuell , array |
|---|---|
| Designad av | Gary D. Knott, Daniel R. Kerner och Barry Bunow |
| Utvecklare | Civiliserad programvara |
| Dök först upp | sent 1970-tal |
| Maskinskrivningsdisciplin | dynamisk , svag |
| OS | Cross-plattform |
| Hemsida | |
| |
MLAB ( M odeling LAB oratory) är en multiparadigm numerisk datormiljö och fjärde generationens programmeringsspråk utvecklades ursprungligen vid National Institutes of Health .
Ett proprietärt programmeringsspråk utvecklat av Civilized Software, Inc., MLAB tillåter matrismanipulationer , plottning av funktioner och data och implementering av algoritmer och ger stöd för kurvanpassning, differentialekvationer, statistik och grafik.
MLAB är avsedd för numerisk beräkning, med speciella faciliteter för vanlig differentialekvationslösning (ODE-lösning) och kurvanpassning (icke-linjär regression.) Den ger mer än trettio kommandotyper och mer än 450 inbyggda funktioner från områdena av elementär matematik, transcendentala funktioner, sannolikhet och statistik, linjär algebra, optimering, klusteranalys, kombinatorik, numerisk input/output och grafik.
De vanliga lågnivåfunktionerna, t.ex. sinus, cosinus, log, etc., finns, liksom funktioner som utför mer komplexa analyser, såsom singularvärdesuppdelning, diskreta Fourier-transformer, lösning av differentialekvationssystem, icke-parametrisk modellering och begränsad icke-linjär optimering, bland många andra. En betydande samling statistiskt orienterade funktioner, såsom de vanligaste fördelningsfunktionerna och deras inverser, ingår, liksom robusta grafskapande funktioner som stödjer grafer för exceptionellt komplexa funktioner.
Många mjukvarupaket kan integrera vanliga differentialekvationer numeriskt, men MLAB är ett av de få som också kan justera parametrar och initiala villkor. MLAB är lika lätt att hantera kurvanpassning, där justeringarna är linjära eller, som är fallet med de flesta differentialekvationsmodeller, olinjära.
MLAB används i stor utsträckning inom akademiska institutioner och forskningsinstitutioner samt industriföretag.
Historia
MLAB utvecklades ursprungligen vid National Institute of Health i slutet av 1970-talet med hjälp av Stanfords SAIL som kördes på Digital Equipment Corporation (DEC) PDP-10- datorer . Skaparna av MLAB grundade Civilized Software, Inc. 1985 och utökade MLAB i slutet av 1980-talet och början av 1990-talet genom tillämpning av småföretagsinnovationsforskningsbidrag .
MLAB antogs först av forskare och praktiker inom biokemi, men spreds snabbt till många andra områden. Det används nu också i utbildning, i synnerhet undervisningen av linjär algebra , numerisk analys , och är populärt bland forskare som är involverade i kemisk kinetikanalys och modellering och kompartmentmodellering inom farmakologisk (inklusive farmakokinetik ) och fysiologisk forskning.
Syntax
MLAB-applikationen är uppbyggd kring MLAB-skriptspråket. Vanlig användning av MLAB-applikationen innebär att man använder kommandofönstret som interaktiva matematiska eller exekverande textfiler (skript) som innehåller MLAB-kod.
Det finns dussintals MLAB-kommandon och hundratals MLAB-funktioner. I huvudsak är MLAB en tolk för ett matematiskt språk på hög nivå med förmågan att bearbeta återkörbara skriptfiler som kallas do-filer.
Exempel
I MLAB kan man definiera en funktion och rita den enligt följande.
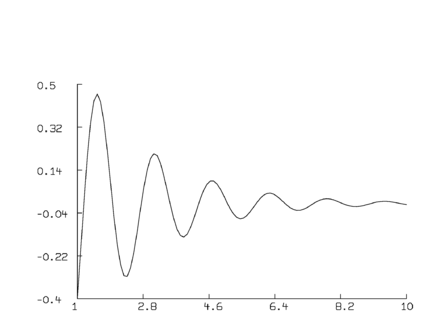
funktion f(x) = a*cos(b*x)*exp(-k*x) a = 1; b=4; k =.5 v=1:10!100 m= points(f,v) draw m view
Resultatet är en enkel plot:
Observera att 1:10!100 = 1:10:0.0909090909, vilket betyder att vi har att göra med en kolumnvektor med värden från 1 till 10 i steg med storleken 0,0909090909
Observera också att points(f,v) = v&'(f på v) , och att v$'(f på v) betyder kolumnvis sammanlänkning av matrisen v med kolumnvektorn av samma storlek som består av värdena av f beräknat på värdena i v .
Man kan läsa in 110 datavärden från en fil till en matris med två kolumner enligt följande (resultatet är en matris med 55 rader för två kolumner.)
d = read("filnamn",55,2)
Om man tar raderna i matrisen d som (x,y) datapunkter - med fel i y-värdena - där dessa datapunkter är "modellerade" av funktionen f , definierad ovan, kan man uppskatta de okända parametrarna a , b , k enligt följande.
passa(a,b,k), f till d
Man kan använda uppskattade vikter för de olika datapunkterna i d baserat på en rörelsevariansuppskattningsfunktion ewt enligt följande.
passa(a,b,k), f till d med wt ewt(d)
Man kan rita upp data och "passformen" enligt följande.
radera w /* för att kassera tidigare bild */ rita d linjetyp ingen, punkttyp cirkel rita punkter(f,d kol 1) färg grön vy
Man kan titta på den symboliska derivatan av f och rita upp den på följande sätt.
typ f'x ritpunkter (f'x, d kol 1) färg röd vy
Observera att MLAB kan använda symboliska derivator när derivatvärden behövs under kurvanpassning eller vid lösning av ODE. Observera också att man kan passa in (eller bara lösa) differentialekvationsdefinierade modeller i MLAB, så att kemisk kinetik och fysiologiska och kompartmentella modeller kan hanteras.