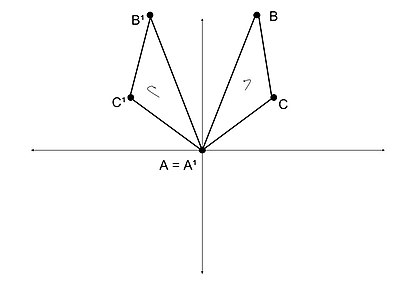
Likhetssystem av trianglar

Ett likhetssystem av trianglar är en specifik konfiguration som involverar en uppsättning trianglar. En uppsättning trianglar anses vara en konfiguration när alla trianglar delar minst en infallsrelation med en av de andra trianglarna som finns i uppsättningen. En incidensrelation mellan trianglar hänvisar till när två trianglar delar en punkt. Till exempel är de två trianglarna till höger, $AHC$ och ${\displaystyle BHC} ,$ en konfiguration som består av två incidentrelationer, eftersom punkterna $C$ och ${\ displaystyle H}$ delas. Trianglarna som utgör konfigurationer kallas komponenttrianglar. Trianglar måste inte bara vara en del av en konfigurationsuppsättning för att vara i ett likhetssystem, utan måste också vara direkt lika. Direkt likhet innebär att alla vinklar är lika mellan två givna trianglar och att de delar samma rotationskänsla. Som framgår av de intilliggande bilderna, i de direkt likartade trianglarna, rotationen av $B$ till $C$ och $B^{1}$ till $C^ {1}$ inträffar i samma riktning. I de motsatta liknande trianglarna sker rotationen av $B$ till $C$ och $B^{1}$ till $C^{1}$ i motsatt riktning. Sammanfattningsvis är en konfiguration ett likhetssystem när alla trianglar i mängden ligger i samma plan och följande gäller: om det finns n trianglar i mängden och n − 1 trianglar är direkt lika, då är n trianglar direkt lika .

Bakgrund

JG Mauldon introducerade idén om likhetssystem för trianglar i sin artikel i Mathematics Magazine "Liknande trianglar". Mauldon började sina analyser med att undersöka givna trianglar $ABC,XYZ$ för direkt likhet genom komplexa tal, närmare bestämt ekvationen ${\begin{vmatrix}a&b&c\\x&y&z\\1&1&1\end{vmatrix}}=0$ . Han fortsatte sedan sina analyser till liksidiga trianglar och visade att om en triangel $ABC$ uppfyllde ekvationen $a+wb+w^{2}c=0$ när $w={\frac {-1+i\surd 3}{2}}$ var det liksidigt. Som bevis på detta arbete tillämpade han sina gissningar om direkt likhet och liksidiga trianglar för att bevisa Napoleons teorem . Han byggde sedan av Napoleon genom att bevisa att om en liksidig triangel konstruerades med liksidiga trianglar som infaller på varje vertex, skapar mittpunkterna på de förbindande linjerna mellan de icke-infallande hörnen av de yttre tre liksidiga trianglarna en liksidig triangel. Annat liknande arbete gjordes av den franske geometern Thébault i hans bevis på att givet ett parallellogram och kvadrater som ligger på vardera sidan av parallellogrammet, skapar kvadraternas mittpunkter en kvadrat. Mauldon analyserade sedan koplanära uppsättningar av trianglar, och bestämde om de var likhetssystem baserat på kriteriet, om alla utom en av trianglarna var direkt lika, då är alla trianglar direkt lika.

Exempel

Trianglar bifogade till en rektangel

Direkt likhet

Om vi konstruerar en rektangel $ABCD$ med direkt likartade trianglar $PAB,QBC,RCD,SDA$ på varje sida av rektangeln som liknar $PQS$ , då är $RQS$ direkt lika och uppsättningen trianglar $\{PAB,QBC,RCD,SDA,PQS,RQS\}$ är ett likhetssystem.

Indirekt likhet

Men om vi erkänner att trianglarna kan vara degenererade och tar punkterna $B$ och $P$ att ligga på varandra och $Q,R,D$ och $S$ att ligga på varandra, då är uppsättningen trianglar inte längre ett direkt likhetssystem eftersom den andra triangeln har area och de andra inte.

Rektangulär parallellepiped

Givet en figur där tre uppsättningar linjer är parallella, men inte likvärdiga i längd (formellt känd som en rektangulär parallellepiped ) med alla ordningspunkter två märkta enligt följande:

\{A_{1}B_{1}C_{1},A_{2}B_{2}C_{2},A_{3}B_{3}C_{3} ,A_{4}B_{4}C_{4},A_{1}B_{4}C_{3},A_{2}B_{3}C_{4},A_{3}B_{2}C_{ 1},A_{4}B_{1}C_{2}\}

Sedan kan vi ta punkterna ovan, analysera dem som trianglar och vi kan visa att de bildar ett likhetssystem.

Bevis:

För att en given triangel, $KLM$ , ska vara direkt lik $A_{1},B_{1},C_{1}$ följande ekvation ska vara nöjd:

(\ell -m)a_{1}+(mk)b_{1}+(k) -1)c_{1}=0.

där ℓ , m , k , a ₁ , b ₁ och c ₁ är sidor av trianglar.

Om samma mönster följs för resten av trianglarna kommer man att märka att summeringen av ekvationerna för de fyra första trianglarna och summeringen av ekvationerna för de fyra sista trianglarna ger samma resultat. Därför, genom definitionen av ett likhetssystem av trianglar, oavsett vilka sju liknande trianglar som väljs, kommer den åttonde att uppfylla systemet, vilket gör dem alla direkt lika.