Kvadratisk obegränsad binär optimering

Quadratic unconstrained binary optimization ( QUBO ), även känd som unconstrained binary quadratic programmering ( UBQP ), är ett kombinatoriskt optimeringsproblem med ett brett utbud av applikationer från finans och ekonomi till maskininlärning . QUBO är ett NP-hårt problem, och för många klassiska problem från teoretisk datavetenskap , som maximal skärning , graffärgning och partitionsproblemet , har inbäddningar i QUBO formulerats. Inbäddningar för maskininlärningsmodeller inkluderar stödvektormaskiner, klustring och probabilistiska grafiska modeller . Dessutom, på grund av sin nära koppling till Ising-modeller , utgör QUBO en central problemklass för adiabatisk kvantberäkning, där den löses genom en fysisk process som kallas kvantglödgning .

Definition

Mängden binära vektorer med en fast längd $n>0$ betecknas med $\mathbb {B} ^{n}$ , där $\mathbb { B} =\lbrace 0,1\rbrace$ är uppsättningen av binära värden (eller bitar ). Vi får en övre triangulär matris med verkligt värde ${\displaystyle Q\in \mathbb {R} ^{n\times n}} ,$ vars poster $Q_{ij}$ definierar en vikt för varje par av index $i,j\in \lbrace 1,\dots ,n\rbrace$ inom den binära vektorn. Vi kan definiera en funktion $f_{Q}:\mathbb {B} ^{n}\rightarrow \mathbb {R}$ som tilldelar ett värde till varje binär vektor genom

f_{Q}(x)=x^{\top }Qx=\summa _ {i=1}^{n}\summa _{j=i}^{n}Q_{ij}x_{i}x_{j}

läggs vikten ${\displaystyle Q_{ij}} till om både$ $x_{i}$ och $x_{j}$ har värde 1. När $i=j}$ ${\$ $x_{ i}x_{i}=x_{i}$ , värdena $Q_{ii}$ läggs till om $x_{i}=1$ , som för alla $x_{i}\in \mathbb {B}$ .

QUBO-problemet består i att hitta en binär vektor $x^{*}$ som är minimal med avseende på $f_{Q}$ , nämligen

x^{*}={\underset {x\in \mathbb {B} ^{n}}{\arg \min }}~f_ {Q}(x)

I allmänhet är $x^{*}$ inte unik, vilket betyder att det kan finnas en uppsättning minimeringsvektorer med lika värde wrt $f_{Q}$ . Komplexiteten hos QUBO uppstår från antalet binära kandidatvektorer som ska utvärderas, som $|\mathbb {B} ^{n}|=2^{n}$ växer exponentiellt i $n$ .

Ibland definieras QUBO som problemet med att maximera $f_{Q}$ , vilket motsvarar att minimera $f_{-Q}=-f_{Q}$ .

Egenskaper

Genom att multiplicera koefficienterna $Q_{ij}$ med en positiv faktor $\alpha >0$ skalas utdata från $f$ i enlighet därmed, vilket lämnar det optimala $x^ {*}$ oförändrad:

f_{\alpha Q}(x)=\sum _{i\leq j}(\alpha Q_{ij})x_{i}x_{j}=\alpha \sum _{i\leq j}Q_{ij }x_{i}x_{j}=\alpha f_{Q}(x)

Om du vänder tecknet för alla koefficienter vänds tecknet för $f$ s utdata, vilket gör $x^{* }$ den binära vektorn som maximerar $f_{-Q}$ :

f_{-Q}(x)=\summa _{i\leq j}(-Q_{ij})x_{i}x_{j}=-\ summa _{i\leq j}Q_{ij}x_{i}x_{j}=-f_{Q}(x)

Om alla koefficienter är positiva är optimum trivialt $x^{*}=(0,\dots ,0)$ . På liknande sätt, om alla koefficienter är negativa, är optimum $x^{*}=(1,\dots ,1)$ .
Om ${\displaystyle \forall i\neq j:~Q_{ij}=0} ,$ dvs. bitarna kan optimeras oberoende, då är motsvarande QUBO-problem lösbart i ${\mathcal {O}}(n)$ , de optimala variabeltilldelningarna $x_{i}^{*}$ är helt enkelt 1 om $Q_{ii}< 0$ och 0 annars.

Ansökningar

QUBO är ett strukturellt enkelt men ändå beräkningssvårt optimeringsproblem. Den kan användas för att koda ett brett utbud av optimeringsproblem från olika vetenskapliga områden.

Klusteranalys

Binär klustring med QUBO

20 points with random cluster assignment

En dålig klusteruppgift.

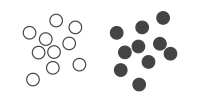
20 points with sensible cluster assignment

Ett bra klusteruppdrag.

Visuell representation av ett klusterproblem med 20 punkter: Cirklar av samma färg tillhör samma kluster. Varje cirkel kan förstås som en binär variabel i motsvarande QUBO-problem.

Som ett illustrativt exempel på hur QUBO kan användas för att koda ett optimeringsproblem, betraktar vi problemet med klusteranalys . Här ges vi en uppsättning av 20 punkter i 2D-rymden, beskrivna av en matris ${\displaystyle D\in \mathbb {R} ^{20\times 2}} ,$ där varje rad innehåller två kartesiska koordinater . Vi vill tilldela varje punkt till en av två klasser eller kluster , så att punkter i samma kluster liknar varandra. För två kluster kan vi tilldela en binär variabel $x_{i}\in \mathbb {B}$ till den punkt som motsvarar den $i$ -th raden i $D$ , som anger om det tillhör det första ( $x_{i}=0$ ) eller det andra klustret ( $x_{i}=1$ ). Följaktligen har vi 20 binära variabler, som bildar en binär vektor $x\in \mathbb {B} ^{20}$ som motsvarar en klustertilldelning av alla punkter (se figur).

Ett sätt att härleda en klustring är att beakta de parvisa avstånden mellan punkter. Givet en klustertilldelning $x$ , värdena $x_{i}x_{j}$ eller $(1-x_{ i})(1-x_{j})$ utvärderas till 1 om punkterna $i$ och $j$ är i samma kluster. På liknande sätt, $x_{i}(1-x_{j})$ eller $(1-x_{i})x_{j}$ indikerar att de finns i olika kluster. Låt $d_{ij}\geq 0$ beteckna det euklidiska avståndet mellan punkterna $i$ och $j$ . För att definiera en kostnadsfunktion att minimera, när punkterna $i$ och $j$ är i samma kluster adderar vi deras positiva avstånd ${\displaystyle d_{ij}} ,$ och subtraherar det när de är i olika kluster. På så sätt tenderar en optimal lösning att placera punkter som är långt ifrån varandra i olika kluster och punkter som ligger nära samma kluster. Kostnadsfunktionen kommer alltså ner på

{\begin{aligned}f(x) &=\summa _{i<j}d_{ij}(x_{i}x_{j}+(1-x_{i})(1-x_{j}))-d_{ij}(x_{i }(1-x_{j})+(1-x_{i})x_{j})\\&=\summa _{i<j}\left[4d_{ij}x_{i}x_{j} -2d_{ij}x_{i}-2d_{ij}x_{j}+d_{ij}\right]\end{aligned}}

Från den andra raden kan QUBO-parametrarna lätt hittas genom att omarrangera till att vara:

{\begin{aligned}Q_{ij }&={\begin{cases}4d_{ij}&{\text{if }}i\neq j\\\sum _{k=1}^{i-1}d_{ki}+\summa _{ \ell =i+1}^{n}d_{i\ell }&{\text{if }}i=j\end{cases}}\end{aligned}}

Genom att använda dessa parametrar kommer den optimala QUBO-lösningen att motsvara en optimal klusterfunktion över kostnaden.

Anslutning till Ising-modeller

QUBO är mycket nära besläktad och beräkningsmässigt ekvivalent med Ising-modellen , vars Hamiltonska funktion definieras som

H(\sigma )=-\summa _{\langle i~j\rangle }J_{ ij}\sigma _{i}\sigma _{j}-\mu \sum _{j}h_{j}\sigma _{j}

med realvärderade parametrar $h_{j},J_{ij},\mu$ för alla $i,j$ . Spinvariablerna $\sigma _{j}$ är binära med värden från $\lbrace -1,+1\rbrace$ istället för $\mathbb {B }$ . Dessutom, i Ising-modellen är variablerna vanligtvis arrangerade i ett gitter där endast angränsande par av variabler $\langle i~j\rangle$ kan ha koefficienter som inte är noll. Att tillämpa identiteten $\sigma \mapsto 2x-1$ ger ett motsvarande QUBO-problem:

{\begin{aligned}f(x)&=\summa _{\langle i~j\rangle }-J_{ij}(2x_{ i}-1)(2x_{j}-1)+\sum _{j}\mu h_{j}(2x_{j}-1)\\&=\summa _{\langle i~j\rangle } -4J_{ij}x_{i}x_{j}+2J_{ij}x_{i}+2J_{ij}x_{j}-J_{ij}+\summa _{j}2\mu h_{j} x_{j}-\mu h_{j}&&{\text{med }}x_{j}=x_{j}x_{j}\\&=\summa _{i=1}^{n}\summa _{j=1}^{i}q_{ij}x_{i}x_{j}+C\end{aligned}}

var

{\begin{aligned}Q_{ij}&={\begin{cases}-4J_{ij}&{\text{if }}i\neq j\\\ summa _{\langle k~i\rangle }2J_{ki}+\sum _{\langle i~\ell \rangle }2J_{i\ell }+2\mu h_{i}&{\text{if } }i=j\end{cases}}\\C&=-\sum _{\langle i~j\rangle }J_{ij}-\sum _{j}\mu h_{j}\end{aligned}}

Eftersom konstanten $C$ inte ändrar positionen för det optimala ${\displaystyle x^{*}} ,$ kan den försummas under optimering och är endast viktig för att återställa det ursprungliga Hamiltonska funktionsvärdet.

externa länkar

QUBO Benchmark (riktmärke av mjukvarupaket för den exakta lösningen av QUBOs; del av den välkända Mittelmann benchmark-samlingen)

Endre Boros, Peter L Hammer & Gabriel Tavares (april 2007). "Lokal sökheuristik för Quadratic Unconstrained Binary Optimization (QUBO)" . Journal of Heuristics . Föreningen för Datormaskiner. 13 (2): 99–132. doi : 10.1007/s10732-007-9009-3 . S2CID 32887708 . Hämtad 12 maj 2013 .
Di Wang & Robert Kleinberg (november 2009). "Analysera kvadratiska obegränsade binära optimeringsproblem via multivaruflöden" . Diskret tillämpad matematik . Elsevier. 157 (18): 3746–3753. doi : 10.1016/j.dam.2009.07.009 . PMC 2808708 . PMID 20161596 .