Kotzigs sats
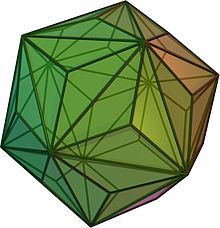
Inom grafteori och polyedrisk kombinatorik , områden inom matematiken, är Kotzigs teorem påståendet att varje polyedrisk graf har en kant vars två ändpunkter har totalgraden högst 13. Ett extremfall är triakis icosahedron , där ingen kant har mindre totalgrad. Resultatet är uppkallat efter Anton Kotzig , som publicerade det 1955 i den dubbla formen att varje konvex polyeder har två intilliggande ytor med totalt högst 13 sidor. Det namngavs och populariserades i väster på 1970-talet av Branko Grünbaum .
Mer generellt har varje plan graf med minsta grad minst tre antingen en kant på total grad som högst 12, eller minst 60 kanter som (liksom kanterna i triakis icosahedron) förbinder hörn av grader 3 och 10. Om alla triangulära ytor av en polyeder är hörn-disjunkta, det finns en kant med mindre total grad, högst åtta. Generaliseringar av satsen är också kända för grafinbäddningar på ytor med högre genus .
Satsen kan inte generaliseras till alla plana grafer , eftersom de kompletta tvådelade graferna och har kanter med obegränsad total grad. Men för plana grafer med hörn av grad lägre än tre, har varianter av satsen bevisats, vilket visar att antingen finns det en kant av begränsad totalgrad eller någon annan speciell typ av subgraf.

