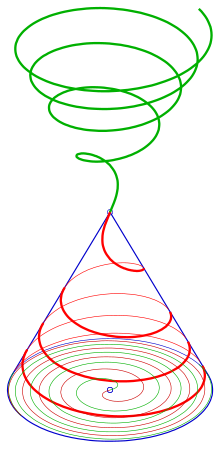
Konisk spiral

Konisk spiral med arkimedisk spiral som planlösning

planlösning: Fermats spiral

planlösning: logaritmisk spiral

planlösning: hyperbolisk spiral

I matematik är en konisk spiral , även känd som en konisk spiral , en rymdkurva på en rät cirkulär kon , vars planlösning är en plan spiral . Om planlösningen är en logaritmisk spiral kallas den conchospiral (av conch ).

Parametrisk representation

I $x$ - $y$ -planet en spiral med parametrisk representation

$x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi$

en tredje koordinat ${ \displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ m>0\;}$$\displaystyle z(\varphi )}$ kan läggas till så att rymdkurvan ligger på konen med ekvation :

• $x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .$

Sådana kurvor kallas koniska spiraler. De var kända för Pappos .

Parameter $m$ är lutningen av konens linjer i förhållande till $x$ - $y$ -planet.

En konisk spiral kan istället ses som den ortogonala projektionen av planritningsspiralen på konen.

Exempel

1) Börjar med en arkimedisk spiral $\;r(\varphi )=a\varphi \;$ ger den koniska spiralen (se diagram)

$x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .$

I detta fall kan den koniska spiralen ses som skärningskurvan för konen med en skruvlinje .

2) Det andra diagrammet visar en konisk spiral med en Fermats spiral $\;r(\varphi )=\pm a{\sqrt {\varphi }}\;$ som planritning.

3) Det tredje exemplet har en logaritmisk spiral $\;r(\varphi )=ae^{k\varphi }\;$ som planlösning. Dess speciella egenskap är dess konstanta lutning (se nedan).

Att introducera förkortningen $K=e^{k}$ ger beskrivningen: $r(\varphi )=aK^{\varphi }$ .

4) Exempel 4 är baserat på en hyperbolisk spiral $\;r(\varphi )=a/\varphi \;$ . En sådan spiral har en asymptot (svart linje), vilket är planlösningen för en hyperbel (lila). Den koniska spiralen närmar sig hyperbeln för $\varphi \to 0$ .

Egenskaper

Följande undersökning behandlar koniska spiraler av formen $r=a\varphi ^{n}$ respektive $r=ae^{k\varphi }$ . .

Backe

Lutningsvinkel vid en punkt i en konisk spiral

Lutningen vid en punkt i en konisk spiral är lutningen för denna punkts tangent med avseende på $x$ - $\displaystyle y}$ { -planet. Motsvarande vinkel är dess lutningsvinkel (se diagram):

$\tan \beta ={\frac {z'}{\sqrt {(x')^{2}+(y')^{2}}}}={\frac {mr'}{\sqrt {(r')^{2}+r^{2}}}}\ .$

En spiral med $r=a\varphi ^{n}$ ger:

• $\tan \beta ={\frac {mn}{\sqrt {n^{2}+\varphi ^{2}}}}\ .$

För en arkimedisk spiral är $n=1$ och därför är dess lutning $\ \tan \beta ={\tfrac {m}{\sqrt {1+\varphi ^{2}}}}\ .$

• För en logaritmisk spiral med $r=ae^{k\varphi }$ är lutningen $\ \tan \beta ={\tfrac { mk}{\sqrt {1+k^{2}}}}\$ ( $\color {röd}{\text{ konstant!}}$ ).

På grund av denna egenskap kallas en conchospiral en likvinklig konisk spiral.

Båglängd

Längden på en båge av en konisk spiral kan bestämmas av

$L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(x')^{2}+(y')^{2}+(z' )^{2}}}\,\mathrm {d} \varphi =\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {(1+m^{2}) (r')^{2}+r^{2}}}\,\mathrm {d} \varphi \ .$

För en arkimedisk spiral kan integralen lösas med hjälp av en tabell med integraler , analogt med det plana fallet:

$L={\frac {a}{2}}{\big [}\varphi {\sqrt {(1+m^{2})+\varphi ^{2}}}+(1+m^ {2})\ln {\big (}\varphi +{\sqrt {(1+m^{2})+\varphi ^{2}}}{\big )}{\big ]}_{\varphi _{1}}^{\varphi _{2}}\ .$

För en logaritmisk spiral kan integralen enkelt lösas:

$L={\frac {\sqrt {(1+m^{2})k^{2}+1}}{k}}(r{\big (}\varphi _{2})-r (\varphi _{1}){\big )}\ .$

I andra fall förekommer elliptiska integraler .

Utveckling

Utveckling (grön) av en konisk spiral (röd), höger: en sidovy. Planet som innehåller utvecklingen är designat av $\pi$ . Inledningsvis rör konen och planet vid den lila linjen.

För utveckling av en konisk spiral avståndet $\rho (\varphi )$ för en kurvpunkt $(x,y,z)$ till konens spets $(0,0,z_{0})$ och förhållandet mellan vinkeln $\varphi$ och motsvarande vinkel $\psi$ för utvecklingen måste bestämmas:

$\rho ={\sqrt {x^{2}+y^{2}+(z-z_{0} )^{2}}}={\sqrt {1+m^{2}}}\;r\ ,$

$\varphi ={\sqrt {1+m^{2}}}\psi \ .$

Därför är den polära representationen av den utvecklade koniska spiralen:

• $\rho (\psi )={\sqrt {1+m^{2}}}\;r({\sqrt {1+ m^{2}}}\psi )$

I fallet med $r=a\varphi ^{n}$ är den polära representationen av den utvecklade kurvan

$\rho =a{\sqrt {1+m^{2}}}^{\,n+1}\psi ^{n},$

som beskriver en spiral av samma typ.

• Om planlösningen för en konisk spiral är en arkimedisk spiral är dess utveckling en arkimedisk spiral.

I fallet med en hyperbolisk spiral ( $n=-1$ ) är utvecklingen kongruent med planritningsspiralen.

I fallet med en logaritmisk spiral $r=ae^{k\varphi }$ är utvecklingen en logaritmisk spiral:

$\rho =a{\sqrt {1+m^{2}}}\;e^{k{\sqrt {1+m^{2}}}\psi }\ .$

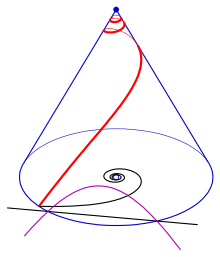
Tangent spår

Spåret (lila) av tangenterna i en konisk spiral med en hyperbolisk spiral som planritning. Den svarta linjen är asymptoten för den hyperboliska spiralen.

Samlingen av skärningspunkter för tangenterna i en konisk spiral med $x$ - $y$ -planet (planet genom konens spets) kallas dess tangentspår .

För den koniska spiralen

$(r\cos \varphi ,r\sin \varphi ,mr)$

tangentvektorn är

$(r'\cos \varphi -r\sin \varphi ,r'\sin \ varphi +r\cos \varphi ,mr')^{T}$

och tangenten:

$x(t)=r\cos \varphi +t(r'\cos \varphi -r\sin \varphi )\ ,$

$y(t)=r\sin \varphi +t(r'\sin \varphi +r\cos \varphi )\ ,$

$z(t)=mr+tmr'\ .$

Skärningspunkten med $x$ - $y$ -planet har parametern $t=-r/r'$ och skärningspunkten är

• $\left({\frac {r^{2}}{r'}}\sin \varphi ,-{\frac {r^{2}}{r'}}\cos \varphi ,0\right )\ .$

$r=a\varphi ^{n}$ ger $\ {\tfrac {r^{2}}{r'}}= {\tfrac {a}{n}}\varphi ^{n+1}\$ och tangentspåret är en spiral. I fallet $n=-1$ (hyperbolisk spiral) degenererar tangentspåret till en cirkel med radien $a$ (se diagram). För $r=ae^{k\varphi }$ har man $\ {\tfrac {r^{2}}{r'}}={ \tfrac {r}{k}}\$ och tangentspåret är en logaritmisk spiral, som är kongruent med planritningen, på grund av självlikheten hos en logaritmisk spiral.

Snigelskal ( Neptunea angulata vänster, höger: Neptunea despecta

externa länkar

• Jamnitzer -Galerie: 3D-Spiralen. .
• Weisstein, Eric W. "Konisk spiral" . MathWorld .