Katalanska triangeln

I kombinatorisk matematik är den katalanska triangeln en taltriangel vars poster $C(n,k)$ ger antalet strängar som består av n X och k Y så att inget initialt segment av strängen har fler Y än X. Det är en generalisering av de katalanska siffrorna och är uppkallad efter Eugène Charles Catalan . Bailey visar att $C(n,k)$ uppfyller följande egenskaper:

1. $C(n,0)=1{\text{ för }}n\geq 0$ .
2. $C(n,1)=n{\text{ för }}n\geq 1$ .
3. $C(n+1,k)=C(n+ 1,k-1)+C(n,k){\text{ för }}1<k<n+1$
4. $C(n+1,n+1)=C(n+1,n){\text{ för }}n\geq 1$ .

Formel 3 visar att inmatningen i triangeln erhålls rekursivt genom att lägga till tal till vänster och ovanför triangeln. Det tidigaste utseendet på den katalanska triangeln tillsammans med rekursionsformeln finns på sidan 214 i avhandlingen om kalkyl som publicerades 1800 av Louis François Antoine Arbogast .

Shapiro introducerar en annan triangel som han kallar den katalanska triangeln som är skild från den triangel som diskuteras här.

Allmän formel

Den allmänna formeln för $C(n,k)$ ges av

$C(n,k)={\binom {n+k}{k}}-{\binom {n +k}{k-1}}$

Så

$C(n,k)={\frac {n-k+1}{n+1}}{\binom {n+k}{k}}$

När ${\displaystyle k=n} är$ diagonalen C ( n , n ) det n :e katalanska talet .

Radsumman för den n :e raden är det ( n + 1) -: e katalanska numret , med hjälp av hockeyklubbans identitet och ett alternativt uttryck för katalanska tal.

Vissa värden ges av

k n	0	1	2	3	4	5	6	7	8
0	1
1	1	1
2	1	2	2
3	1	3	5	5
4	1	4	9	14	14
5	1	5	14	28	42	42
6	1	6	20	48	90	132	132
7	1	7	27	75	165	297	429	429
8	1	8	35	110	275	572	1001	1430	1430

En kombinatorisk tolkning av $(n,k-1)$ -th värdet är antalet icke-minskande partitioner med exakt n delar med maximal del k så att varje del är mindre än eller lika med dess index. Så, till exempel, $(4,2)=9$ räkningar

${\displaystyle 1111,1112,1113,1122,1123,12233,13213,11232,13213,1123,12323,1123,1123,12323,1123,1123,12323,12323,12323$

Generalisering

Katalanska trapetser är en räknebar uppsättning antal trapetser som generaliserar den katalanska triangeln. Katalanska trapets av ordningen m = 1, 2, 3, ... är en taltrapets vars poster $C_{m}(n,k)$ ger antalet strängar som består av n Xs och k Ys så att i varje initial segment av strängen antalet Ys inte överstiger antalet X med m eller mer. Per definition är katalanska trapets av ordningen m = 1 katalanska triangeln, dvs $C_{1}(n,k)=C(n,k)$ .

Vissa värden på katalanska trapets av ordningen m = 2 ges av

k n	0	1	2	3	4	5	6	7	8
0	1	1
1	1	2	2
2	1	3	5	5
3	1	4	9	14	14
4	1	5	14	28	42	42
5	1	6	20	48	90	132	132
6	1	7	27	75	165	297	429	429
7	1	8	35	110	275	572	1001	1430	1430

Vissa värden på katalanska trapets av ordningen m = 3 ges av

k n	0	1	2	3	4	5	6	7	8	9
0	1	1	1
1	1	2	3	3
2	1	3	6	9	9
3	1	4	10	19	28	28
4	1	5	15	34	62	90	90
5	1	6	21	55	117	207	297	297
6	1	7	28	83	200	407	704	1001	1001
7	1	8	36	119	319	726	1430	2431	3432	3432

Återigen är varje element summan av det ovanför och det till vänster.

En allmän formel för $C_{m}(n,k)$ ges av

$C_{m}(n,k)={\begin{cases}\left({\begin{array}{c}n+k\\k\end{array}}\right)&\,\ ,\,0\leq k<m\\\\\left({\begin{array}{c}n+k\\k\end{array}}\right)-\left({\begin{array} {c}n+k\\km\end{array}}\right)&\,\,\,m\leq k\leq n+m-1\\\\0&\,\,\,k>n +m-1\end{cases}}$

( n = 0, 1, 2, ... , k = 0, 1, 2, ... , m = 1, 2, 3, ... ).

Bevis för den allmänna formeln för $C_{m}(n,k)$

Bevis 1

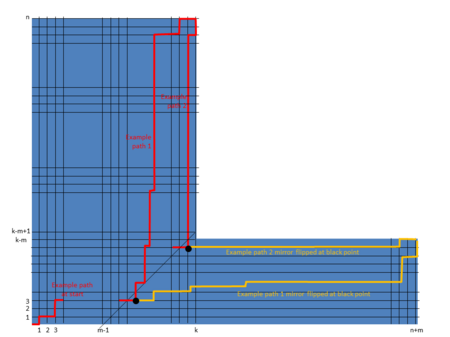
Detta bevis innebär en utvidgning av Andres Reflection-metoden som används i det andra beviset för det katalanska talet till olika diagonaler. Följande visar hur varje väg från det nedre vänstra $(0,0)$ till det övre högra $(k,n)$ i diagrammet som korsar begränsningen $n-k+m-1=0$ kan också reflekteras till slutpunkten $(n+m,km)$ .

Vi överväger tre fall för att bestämma antalet vägar från $(0,0)$ till $(k,n)$ som inte korsar begränsningen:

(1) när $m>k$ kan begränsningen inte korsas, så alla vägar från $(0,0)$ till $(k,n)$ är giltiga, dvs $C_{m}(n,k)=\left({\begin{array}{c}n+k\\k \end{array}}\right)$ .

(2) när $k-m+1>n$ är det omöjligt att bilda en väg som inte korsar begränsningen, dvs. $C_{ m}(n,k)=0$ .

(3) när $m\leq k\leq n+m-1$ , då $C_{m}(n,k)$ är antalet 'röda' banor $\left({\begin{array}{c}n+k\\k\end{array}}\right)$ minus antalet ' gula' banor som korsar begränsningen, dvs $\left({\begin{array}{c}( n+m)+(km)\\km\end{array}}\right)=\left({\begin{array}{c}n+k\\km\end{array}}\right)$ .

Därför antalet sökvägar från $(0,0)$ till $(k,n)$ som inte korsar begränsningen $n-k+m-1=0$ är som anges i formeln i föregående avsnitt " Generalisering ".

Bevis 2

Först bekräftar vi giltigheten av återfallsrelationen $C_{m}(n,k)= C_{m}(n-1,k)+C_{m}(n,k-1)$ genom att bryta ner $C_{m}(n,k)$ i två delar , den första för XY-kombinationer som slutar på X och den andra för de som slutar på Y. Den första gruppen har därför $C_{m}(n-1,k)$ giltiga kombinationer och den andra har $C_{m}(n,k-1)$ . Bevis 2 slutförs genom att verifiera att lösningen uppfyller återfallsrelationen och följer initiala villkor för $C_{m}(n,0)$ och $\displaystyle C_{m} (0,k)}$ .