Isoperimetrisk punkt
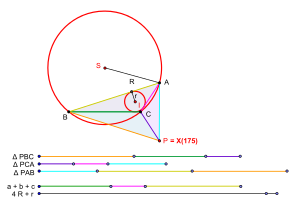
I geometri är den isoperimetriska punkten en speciell punkt som är associerad med en plan triangel . Termen introducerades ursprungligen av GR Veldkamp i en artikel publicerad i American Mathematical Monthly 1985 för att beteckna en punkt P i planet för en triangel ABC som har egenskapen att trianglarna PBC , PCA och PAB har isoperimetrar, dvs. egendom som
- PB + BC + CP = PC + CA + AP = PA + AB + BP .
Isoperimetriska punkter i betydelsen Veldkamp existerar endast för trianglar som uppfyller vissa villkor. Den isoperimetriska punkten för triangeln ABC i betydelsen Veldkamp, om den finns, har följande trilinjära koordinater .
- ( sek ( A /2 ) cos ( B /2 ) cos ( C /2 ) − 1 , sek ( B / 2 ) cos ( C / 2 ) cos ( A / 2 ) - 1 , sek ( C / 2 ) cos ( A /2 ) cos ( B /2 ) − 1 )
Givet vilken triangel ABC som helst kan man associera med den en punkt P som har trilinjära koordinater enligt ovan. Denna punkt är ett triangelcentrum och i Clark Kimberlings Encyclopedia of Triangle Centers ( ETC) kallas det den isoperimetriska punkten för triangeln ABC . Den betecknas som triangelcentrum X(175). Punkten X(175) behöver inte vara en isoperimetrisk punkt i triangeln ABC i betydelsen Veldkamp. Men om isoperimetrisk punkt i triangeln ABC i betydelsen Veldkamp existerar, så skulle den vara identisk med punkten X(175).
Punkten P med egenskapen att trianglarna PBC , PCA och PAB har lika omkrets har studerats redan 1890 i en artikel av Emile Lemoine .
Existens av isoperimetrisk punkt i betydelsen Veldkamp
Låt ABC vara vilken triangel som helst. Låt sidlängderna för denna triangel vara a , b , och c . Låt dess cirkumradius vara R och inradius vara r . Det nödvändiga och tillräckliga villkoret för existensen av en isoperimetrisk punkt i betydelsen Veldkamp kan anges enligt följande.
- Triangeln ABC har en isoperimetrisk punkt i betydelsen Veldkamp om och endast om a + b + c > 4 R + r .
För alla spetsvinklade trianglar ABC har vi a + b + c > 4 R + r , och därför har alla spetsvinklade trianglar isoperimetriska punkter i betydelsen Veldkamp.
Egenskaper
Låt P beteckna triangelns centrum X(175) i triangeln ABC .
- P ligger på linjen som förenar centrum och Gergonne-punkten i triangeln ABC .
- Om P är en isoperimetrisk punkt i triangeln ABC i betydelsen Veldkamp, så är trianglarnas excirklar PBC , PCA , PAB parvis tangenter till varandra och P är deras radikala centrum.
- Om P är en isoperimetrisk punkt i triangeln ABC i betydelsen Veldkamp, så är omkretsen av trianglarna PBC , PCA , PAB lika med 2 Δ / |( 4 R + r - ( a + b + c ) )| där Δ är arean, R är cirkumradien, r är inradius och a , b , c är sidolängderna av triangeln ABC .
Soddy cirklar
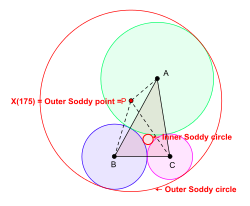
Givet en triangel ABC kan man rita cirklar i triangelns ABC- plan med centrum vid A , B och C så att de tangerar varandra externt. I allmänhet kan man rita två nya cirklar så att var och en av dem är tangentiell till de tre cirklarna med A , B , C som centrum. (En av cirklarna kan urarta till en rak linje.) Dessa cirklar är Soddy-cirklarna i triangeln ABC . Cirkeln med den mindre radien är den inre Soddy-cirkeln och dess centrum kallas den inre Soddy-punkten eller inre Soddy-centrum i triangeln ABC . Cirkeln med den större radien är den yttre Soddy-cirkeln och dess centrum kallas den yttre Soddy-punkten eller yttre Soddy-centrum i triangeln ABC .
Triangelns centrum X(175), den isoperimetriska punkten i betydelsen Kimberling, är den yttre Soddy-punkten i triangeln ABC .
externa länkar
- isoperimetriska och lika omvägspunkter - interaktiv illustration på Geogebratube