Intransitiv tärning
En uppsättning tärningar är intransitiv (eller icke-transitiv) om den innehåller tre tärningar, A , B , och C , med egenskapen att A slår högre än B mer än halva tiden och B slår högre än C mer än halva tiden, men det är inte sant att A rullar högre än C mer än halva tiden. Med andra ord, en uppsättning tärningar är intransitiv om den binära relationen – X kastar ett högre tal än Y mer än halva tiden – på dess element inte är transitiv . Enklare, A slår normalt B , B slår normalt C , men A slår normalt inte C .
Det är möjligt att hitta tärningssatser med den ännu starkare egenskapen att det för varje tärning i setet finns en annan tärning som slår ett högre antal än den mer än halva tiden. Detta är annorlunda genom att istället för att bara " A slår normalt inte C " är det nu " C slår normalt A" Genom att använda en sådan uppsättning tärningar kan man uppfinna spel som är partiska på ett sätt som människor som inte är vana vid intransitiva tärningar kanske inte förväntar sig (se exempel ).
Exempel
Tänk på följande uppsättning tärningar.
- Matris A har sidorna 2, 2, 4, 4, 9, 9.
- Die B har sidorna 1, 1, 6, 6, 8, 8.
- Die C har sidorna 3, 3, 5, 5, 7, 7.
Sannolikheten att A slår 5/9 ett B högre tal än B , sannolikheten att slår högre än C och sannolikheten att C slår högre än A är alla , så denna uppsättning tärningar är intransitiv. Faktum är att det har den ännu starkare egenskapen att det för varje tärning i setet finns en annan tärning som slår ett högre antal än den mer än halva tiden.
Tänk nu på följande spel, som spelas med en uppsättning tärningar.
- Den första spelaren väljer en tärning från setet.
- Den andra spelaren väljer en tärning från de återstående tärningarna.
- Båda spelarna slår sin tärning; spelaren som kastar det högre numret vinner.
Om detta spel spelas med en transitiv uppsättning tärningar är det antingen rättvist eller partiskt till förmån för den första spelaren, eftersom den första spelaren alltid kan hitta en tärning som inte kommer att slås av någon annan tärning mer än halva tiden. Om det spelas med den uppsättning tärningar som 5/9 beskrivs ovan är spelet dock partiskt till förmån för den andra spelaren, eftersom den andra spelaren alltid kan hitta en tärning som kommer att slå den första spelarens tärning med sannolikhet . Följande tabeller visar alla möjliga utfall för alla tre tärningspar.
|
Spelare 1 väljer tärning A Spelare 2 väljer tärning C |
Spelare 1 väljer tärning B Spelare 2 väljer tärning A |
Spelare 1 väljer tärning C Spelare 2 väljer tärning B |
|||||||||||
|
A
C
|
2 | 4 | 9 |
B
A
|
1 | 6 | 8 |
C
B
|
3 | 5 | 7 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | C | A | A | 2 | A | B | B | 1 | C | C | C | ||
| 5 | C | C | A | 4 | A | B | B | 6 | B | B | C | ||
| 7 | C | C | A | 9 | A | A | A | 8 | B | B | B | ||
Kommentar angående likvärdigheten av intransitiv tärning
Även om de tre intransitiva tärningarna A, B, C (första uppsättningen tärningar)
- A: 2, 2, 6, 6, 7, 7
- B: 1, 1, 5, 5, 9, 9
- C: 3, 3, 4, 4, 8, 8
5/9 A > B) = P(B > C) = P ( C > A) =
och de tre intransitiva tärningarna A′, B′, C′ (andra uppsättningen tärningar)
- A′: 2, 2, 4, 4, 9, 9
- B′: 1, 1, 6, 6, 8, 8
- C′: 3, 3, 5, 5, 7, 7
5/9 ) = P ( B′ > C′) = P(C′ > A′) =
vinna mot varandra med lika stor sannolikhet att de inte är likvärdiga. Medan den första uppsättningen tärningar (A, B, C) har en "högsta" tärning, har den andra uppsättningen tärningar en "lägsta" tärning. Att kasta de tre tärningarna i ett set och alltid använda den högsta poängen för utvärdering kommer att visa ett annat vinnande mönster för de två tärningarna. tärningarna den första uppsättningen tärningar kommer tärning B att vinna med högst sannolikhet (11/27 . Med den andra uppsättningen tärningar kommer tärningen C′ 8/27 ) A och och C vinner vardera med en sannolikhet på ) och tärningarna A att på vinna med lägst sannolikhet ( 10/27 7/27 ′ och B′ vinner vardera med en sannolikhet .
Variationer
Efrons tärningar
Efrons tärningar är en uppsättning av fyra intransitiva tärningar som uppfanns av Bradley Efron .
De fyra tärningarna A, B, C, D har följande siffror på sina sex ytor:
- A: 4, 4, 4, 4, 0, 0
- B: 3, 3, 3, 3, 3, 3
- C: 6, 6, 2, 2, 2, 2
- D: 5, 5, 5, 1, 1, 1
Sannolikheter
Varje tärning slås av den föregående tärningen i listan, med en 2/3 : sannolikhet på

B:s värde är konstant; A slår den på . 2/3 kast eftersom fyra av dess sex sidor är högre
På samma sätt slår B C med 2 / 3 sannolikhet eftersom endast två av C:s ansikten är högre.
P(C>D) kan beräknas genom att summera betingade sannolikheter för två händelser:
- C rullar 6 ( sannolikhet 1/3 ) ; vinner oavsett D (sannolikhet 1)
- 2 (sannolikhet 2/3 ) ; vinner bara om D slår 1 ( sannolikhet 1/2 )
Den totala sannolikheten för vinst för C är därför
Med en liknande beräkning är sannolikheten att D vinner över A
Bästa total die
De fyra tärningarna har olika sannolikheter att slå en tärning vald slumpmässigt bland de återstående tre:
Som bevisats ovan, slår tärning A B två tredjedelar av tiden men slår D bara en tredjedel av tiden. Sannolikheten att tärning A slår C är 4/9 ) . (A måste slå 4 och C måste slå 2 Så sannolikheten för att A slår någon annan slumpmässigt utvald tärning är:
På samma sätt slår tärning B C två tredjedelar av tiden men slår A bara en tredjedel av tiden. Sannolikheten att tärning B slår D är 1/2 ) . ( endast när D slår 1 Så sannolikheten för att B slår någon annan slumpmässigt utvald tärning är:
Die C slår D två tredjedelar av tiden men slår B bara en tredjedel av tiden. Sannolikheten att tärning C slår 5/9 . A är Så sannolikheten för att C slår någon annan slumpmässigt utvald tärning är:
Slutligen slår tärning D A två tredjedelar av tiden men slår C bara en tredjedel av tiden. Sannolikheten att tärning D slår B är 1/2 ) . ( endast när D slår 5 Så sannolikheten för att D slår någon annan slumpmässigt utvald tärning är:
Därför är den bästa totala tärningen C med en vinstsannolikhet på 0,5185. C rullar också det högsta medeltalet i absoluta tal, 3 + 1 / 3 . 2 + 2/3 ( ) A:s medelvärde är , medan B och D båda är 3.
Varianter med lika medelvärden
Observera att Efrons tärningar har olika 8/3 medelslag . , : genomsnittliga det genomsnitt 10/3 kast av A är , medan B och D vardera i genomsnitt är 9/3 och C är i Den intransitiva egenskapen beror på vilka ytor som är större eller mindre, men beror inte på ytornas absoluta storlek. Därför kan man hitta varianter av Efrons tärningar där oddsen att vinna är oförändrade, men alla tärningar har samma genomsnittliga kast. Till exempel,
- A: 7, 7, 7, 7, 1, 1
- B: 5, 5, 5, 5, 5, 5
- C: 9, 9, 3, 3, 3, 3
- D: 8, 8, 8, 2, 2, 2
Dessa varianttärningar är användbara, t.ex. för att introducera eleverna till olika sätt att jämföra slumpvariabler (och hur man jämför endast medelvärden kan förbise väsentliga detaljer).
Numrerade 1 till 24 tärningar
En uppsättning av fyra tärningar som använder alla siffrorna 1 till 24 kan göras för att vara intransitiv. Med intilliggande par är sannolikheten för en tärning att vinna 2/3.
För rullande högt tal slår B A, C slår B, D slår C, A slår D.
- A: 1, 2, 16, 17, 18, 19
- B: 3, 4, 5, 20, 21, 22
- C: 6, 7, 8, 9, 23, 24
- D: 10, 11, 12, 13, 14, 15
Relation till Efrons tärningar
Dessa tärningar är i grunden desamma som Efrons tärningar, eftersom varje nummer i en serie av på varandra följande nummer på en enda tärning alla kan ersättas med det lägsta numret i serien och sedan omnumrera dem.
- A: 1, 2, 16, 17, 18, 19 → 1, 1, 16, 16, 16, 16 → 0, 0, 4, 4, 4, 4
- B: 3, 4, 5, 20, 21, 22 → 3, 3 , 3, 20, 20, 20 → 1, 1, 1, 5, 5, 5
- C: 6, 7, 8, 9, 23, 24 → 6, 6, 6, 6, 23, 23 → 2, 2, 2, 2, 6, 6
- D: 10, 11, 12, 13, 14, 15 → 10, 10, 10, 10, 10, 10 → 3, 3, 3, 3, 3, 3
Miwins tärningar
Miwins tärning uppfanns 1975 av fysikern Michael Winkelmann.
Betrakta en uppsättning av tre tärningar, III, IV och V så att
- die III har sidorna 1, 2, 5, 6, 7, 9
- tärningen IV har sidorna 1, 3, 4, 5, 8, 9
- matrisen V har sidorna 2, 3, 4, 6, 7, 8
Sedan:
- sannolikheten att III kastar är 17/36 ett högre nummer än IV
- sannolikheten att IV kastar ett högre nummer än V är 17/36
- sannolikheten att V slår ett högre tal än III är 17/36
Set med tre tärningar med minimala ändringar av standardtärningar
Följande intransitiva tärningar har bara ett fåtal skillnader jämfört med 1 till 6 standardtärningar:
- som med standardtärningar är det totala antalet kärnor alltid 21
- som med standardtärningar har sidorna bara pipnummer mellan 1 och 6
- ansikten med samma antal kärnor förekommer max två gånger per tärning
- endast två sidor på varje tärning har nummer som skiljer sig från standardtärningar:
- A: 1, 1 , 3, 5 , 5, 6
- B: 2, 3, 3 , 4, 4 , 5
- C: 1, 2, 2 , 4, 6, 6
Liksom Miwins set är sannolikheten att A vinner mot B (eller B mot C, C mot A ) 17/36 . Sannolikheten för oavgjort är dock . 4/36 , så att endast 15 av 36 kast förlorar Så den totala vinstförväntningen är högre.
Warren Buffett
Warren Buffett är känd för att vara ett fan av intransitiva tärningar. I boken Fortune's Formula: The Untold Story of the Scientific Betting System that Beat the Casinos and Wall Street beskrivs en diskussion mellan honom och Edward Thorp . Buffett och Thorp diskuterade sitt gemensamma intresse för intransitiv tärning. "Detta är en matematisk nyfikenhet, en typ av "trick"-tärningar som förvirrar de flesta människors idéer om sannolikhet."
Buffett försökte en gång vinna ett tärningsspel med Bill Gates med intransitiv tärning. "Buffett föreslog att var och en av dem skulle välja en av tärningarna och sedan kasta de andra två. De skulle satsa på vem som skulle kasta det högsta numret oftast. Buffett erbjöd sig att låta Gates välja sin tärning först. Detta förslag väckte omedelbart Gates nyfikenhet. Han bad att undersöka tärningarna, varefter han krävde att Buffett skulle välja först."
2010 citerade tidningen Wall Street Journal Sharon Osberg, Buffetts bridgepartner, och sa att när hon först besökte hans kontor 20 år tidigare, lurade han henne att spela ett spel med intransitiva tärningar som inte gick att vinna och "tyckte att det var lustigt".
Intransitiv tärning för mer än två spelare
Ett antal personer har introducerat varianter av intransitiva tärningar där man kan tävla mot mer än en motståndare.
Tre spelare
Oskar tärningar
Oskar van Deventer introducerade en uppsättning med sju tärningar (alla ansikten med sannolikhet 1/6 ) : enligt följande
- A: 2, 2, 14, 14, 17, 17
- B: 7, 7, 10, 10, 16, 16
- C: 5, 5, 13, 13, 15, 15
- D: 3, 3, 9, 9, 21, 21
- E: 1, 1, 12, 12, 20, 20
- F: 6, 6, 8, 8, 19, 19
- G: 4, 4, 11, 11, 18, 18
Man kan verifiera att A slår {B,C,E}; B slår {C,D,F}; C slår {D,E,G}; D slår {A,E,F}; E slår {B,F,G}; F slår {A,C,G}; G slår {A,B,D}. Följaktligen, för godtyckligt valda två tärningar finns det en tredje som slår dem båda. Nämligen,
- G slår {A,B}; F slår {A,C}; G slår {A,D}; D slår {A,E}; D slår {A,F}; F slår {A,G};
- A slår {B,C}; G slår {B,D}; A slår {B,E}; E slår {B,F}; E slår {B,G};
- B slår {C,D}; A slår {C,E}; B slår {C,F}; F slår {C,G};
- C slår {D,E}; B slår {D,F}; C slår {D,G};
- D slår {E,F}; C slår {E,G};
- E slår {F,G}.
Oavsett vad de två motståndarna väljer, kommer den tredje spelaren att hitta en av de återstående tärningarna som slår båda motståndarnas tärningar.
Grime tärningar
Dr James Grime upptäckte en uppsättning med fem tärningar enligt följande:
- A: 2, 2, 2, 7, 7, 7
- B: 1, 1, 6, 6, 6, 6
- C: 0, 5, 5, 5, 5, 5
- D: 4, 4, 4, 4, 4, 9
- E: 3, 3, 3, 3, 8, 8
Man kan verifiera att när spelet spelas med en uppsättning Grime-tärningar:
- A slår B slår C slår D slår E slår A (första kedjan);
- A slår C slår E slår B slår D slår A (andra kedjan).
Men när spelet spelas med två sådana set, förblir den första kedjan densamma (med ett undantag som diskuteras senare) men den andra kedjan är omvänd (dvs. A slår D slår B slår E slår C slår A). Följaktligen, vilken tärning de två motståndarna än väljer, kan den tredje spelaren alltid hitta en av de återstående tärningarna som slår dem båda (så länge som spelaren sedan får välja mellan alternativet med en tärning och alternativet med två tärningar):
Uppsättningar som väljs av motståndarnaVinnande uppsättning tärningar Typ siffra A B E 1 A C E 2 A D C 2 A E D 1 B C A 1 B D A 2 B E D 2 C D B 1 C E B 2 D E C 1
Det finns dock två stora problem med denna uppsättning. Den första är att i två-die-alternativet i spelet, bör den första kedjan förbli exakt densamma för att göra spelet intransitivt. I praktiken slår D faktiskt C. Det andra problemet är att den tredje spelaren måste få välja mellan alternativet med en tärning och alternativet med två tärningar – vilket kan ses som orättvist mot andra spelare.
Korrigerade Grime-tärningar
Ovanstående fråga om att D besegrar C uppstår eftersom tärningarna har 6 sidor istället för 5. Genom att ersätta den lägsta (eller högsta) ytan på varje tärning med "reroll" (R), kommer alla fem tärningarna att fungera exakt som Dr. James Grime tänkt sig. :
- A: R, 2, 2, 7, 7, 7
- B: R, 1, 6, 6, 6, 6
- C: R, 5, 5, 5, 5, 5
- D: R, 4, 4, 4, 4, 9
- E: R, 3, 3, 3, 8, 8
Alternativt kan dessa ytor mappas till en uppsättning femkantiga-trapesoedriska (10-sidiga) tärningar, där varje nummer visas exakt två gånger, eller till en uppsättning icosaedriska (20-sidiga) tärningar, där varje nummer visas fyra gånger. Detta eliminerar behovet av ett "reroll" ansikte.
Denna lösning upptäcktes av Jon Chambers, en australiensisk matematiklärare. [ citat behövs ]
Fyra spelare
Ett set med fyra spelare har ännu inte upptäckts, men det bevisades att ett sådant set skulle kräva minst 19 tärningar.
Intransitiv 4-sidig tärning
Tetraedrar kan användas som tärningar med fyra möjliga resultat .
- Set 1
- A: 1, 4, 7, 7
- B: 2, 6, 6, 6
- C: 3, 5, 5, 8
9/16 ) = P ( B > C) = P(C > A) =
Följande tabeller visar alla möjliga resultat:
|
B
A
|
2 | 6 | 6 | 6 |
|---|---|---|---|---|
| 1 | B | B | B | B |
| 4 | A | B | B | B |
| 7 | A | A | A | A |
| 7 | A | A | A | A |
I "A mot B" vinner A i 9 av 16 fall.
|
C
B
|
3 | 5 | 5 | 8 |
|---|---|---|---|---|
| 2 | C | C | C | C |
| 6 | B | B | B | C |
| 6 | B | B | B | C |
| 6 | B | B | B | C |
I "B mot C" vinner B i 9 av 16 fall.
|
A
C
|
1 | 4 | 7 | 7 |
|---|---|---|---|---|
| 3 | C | A | A | A |
| 5 | C | C | A | A |
| 5 | C | C | A | A |
| 8 | C | C | C | C |
I "C mot A" vinner C i 9 av 16 fall.
- Set 2
- A: 3, 3, 3, 6
- B: 2, 2, 5, 5
- C: 1, 4, 4, 4
P 10/16 , (A > B) = P(B > C) = P(C > A) = 9/16
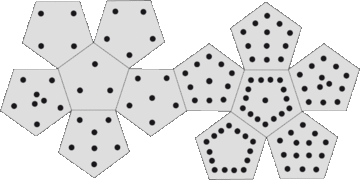
Intransitiv 12-sidig tärning
I analogi med de intransitiva sexsidiga tärningarna finns det också dodekaedrar som fungerar som intransitiva tolvsidiga tärningar . Poängen på var och en av tärningarna resulterar i summan av 114. Det finns inga upprepade tal på var och en av dodekaedrarna.
Miwins dodekaedrar (set 1) vinner cykliskt mot varandra i förhållandet 35:34.
Miwins dodekaedrar (set 2) vinner cykliskt mot varandra i förhållandet 71:67.
Set 1:
| D III | lila | 1 | 2 | 5 | 6 | 7 | 9 | 10 | 11 | 14 | 15 | 16 | 18 | ||||||
| D IV | röd | 1 | 3 | 4 | 5 | 8 | 9 | 10 | 12 | 13 | 14 | 17 | 18 | ||||||
| DV | mörkgrå | 2 | 3 | 4 | 6 | 7 | 8 | 11 | 12 | 13 | 15 | 16 | 17 |
Set 2:
| D VI | cyan | 1 | 2 | 3 | 4 | 9 | 10 | 11 | 12 | 13 | 14 | 17 | 18 | ||||||
| D VII | pärongrön | 1 | 2 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 16 | 17 | 18 | ||||||
| D VIII | ljusgrå | 3 | 4 | 5 | 6 | 7 | 8 | 11 | 12 | 13 | 14 | 15 | 16 |
Intransitiv primnummer med 12-sidiga tärningar
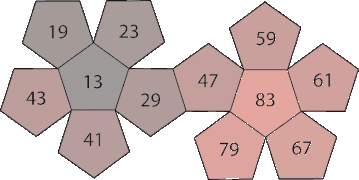
Det är också möjligt att konstruera uppsättningar av intransitiva dodekaedrar så att det inte finns några upprepade tal och alla tal är primtal. Miwins intransitiva primnummerade dodekaedrar vinner cykliskt mot varandra i förhållandet 35:34.
Set 1: Siffrorna summerar till 564.
| PD 11 | grå till blå | 13 | 17 | 29 | 31 | 37 | 43 | 47 | 53 | 67 | 71 | 73 | 83 |
| PD 12 | grått till rött | 13 | 19 | 23 | 29 | 41 | 43 | 47 | 59 | 61 | 67 | 79 | 83 |
| PD 13 | grå till grön | 17 | 19 | 23 | 31 | 37 | 41 | 53 | 59 | 61 | 71 | 73 | 79 |
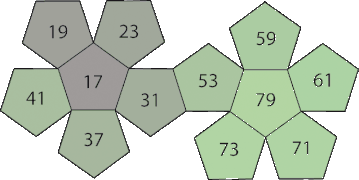
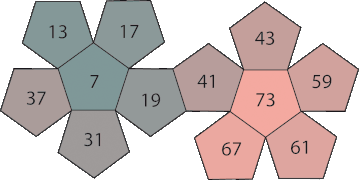
Set 2: Siffrorna summerar till 468.
| PD 1 | oliv till blå | 7 | 11 | 19 | 23 | 29 | 37 | 43 | 47 | 53 | 61 | 67 | 71 |
| PD 2 | kricka till rött | 7 | 13 | 17 | 19 | 31 | 37 | 41 | 43 | 59 | 61 | 67 | 73 |
| PD 3 | lila till grönt | 11 | 13 | 17 | 23 | 29 | 31 | 41 | 47 | 53 | 59 | 71 | 73 |
Se även
Källor
- Gardner, Martin (2001). The Colossal Book of Mathematics: Klassiska pussel, paradoxer och problem: talteori, algebra, geometri, sannolikhet, topologi, spelteori, oändlighet och andra ämnen inom rekreationsmatematiken (första upplagan) . New York: WW Norton & Company. sid. 286 –311. [ ISBN saknas ]
- Spielerische Mathematik mit Miwin'schen Würfeln (på tyska). Bildungsverlag Lemberger. ISBN 978-3-85221-531-0 .
externa länkar
- MathWorld-sidan
- Ivars Petersons MathTrek - Tricky Dice Revisited (15 april 2002)
- Jim Loys pusselsida
- Miwin officiella webbplats (tyska)
- Open Source icke-transitiv tärningssökare
- Non-transitive Dice av James Grime
- mgf.winkelmann Miwins intransitive Dodekaeder
- Matematikutrustning
- Conrey, B., Gabbard, J., Grant, K., Liu, A., & Morrison, K. (2016). Intransitiv tärning. Mathematics Magazine, 89(2), 133-143. Tilldelas av Mathematical Association of America
- Timothy Gowers projekt om intransitiv tärning
- Klarreich, Erica (2023-01-19). "Matematiker slår tärning och skaffar sten-pappersax" . Quanta Magazine .