Integrerande sfär

Stor integrerad sfär för mätning på glödlampor och små lampor

En integrerande sfär (även känd som en Ulbricht-sfär ) är en optisk komponent som består av en ihålig sfärisk hålighet med dess inre täckt med en diffus vit reflekterande beläggning, med små hål för ingångs- och utgångsportar. Dess relevanta egenskap är en enhetlig spridnings- eller spridningseffekt. Ljusstrålar som faller in på någon punkt på den inre ytan fördelas, genom multipla spridningsreflektioner, lika till alla andra punkter. Effekterna av den ursprungliga ljusriktningen minimeras. En integrerande sfär kan ses som en spridare som bevarar kraft men förstör rumslig information. Den används vanligtvis med någon ljuskälla och en detektor för optisk effektmätning. En liknande anordning är fokuseringssfären eller Coblentz-sfären, som skiljer sig genom att den har en spegelliknande (spekulär) inre yta snarare än en diffus inre yta.

1892 publicerade WE Sumpner ett uttryck för genomströmningen av ett sfäriskt hölje med diffust reflekterande väggar. Ř. Ulbricht utvecklade en praktisk realisering av den integrerande sfären, ämnet för en publikation år 1900. Det har blivit ett standardinstrument inom fotometri och radiometri och har fördelen jämfört med en goniofotometer att den totala effekten som produceras av en källa kan erhållas i en enda mätning . Andra former, som en kubisk låda, har också analyserats teoretiskt.

Även små kommersiella integrerande sfärer kostar många tusen dollar, som ett resultat av att deras användning ofta är begränsad till industrin och stora akademiska institutioner. Men 3D-utskrift och hemgjorda beläggningar har sett produktionen av experimentellt exakta DIY-sfärer till mycket låg kostnad.

Teori

Teorin om att integrera sfärer bygger på dessa antaganden:

• Ljus som träffar sfärens sidor sprids på ett diffust sätt, dvs Lambertsreflektans
• Endast ljus som har spridits i sfären träffar portarna eller detektorerna som används för att sondera ljuset

Med dessa antaganden kan sfärmultiplikatorn beräknas. Detta antal är det genomsnittliga antalet gånger en foton sprids i sfären, innan den absorberas i beläggningen eller flyr genom en port. Detta antal ökar med reflektiviteten hos sfärbeläggningen och minskar med förhållandet mellan den totala arean av portar och andra absorberande föremål och sfärens inre area. För att få en hög homogenitet är en rekommenderad sfärmultiplikator 10-25.

Teorin säger vidare att om ovanstående kriterier är uppfyllda så kommer irradiansen på något områdeselement på sfären att vara proportionell mot det totala strålningsflödet som matas in till sfären. Absoluta mätningar av exempelvis ljusflöde kan sedan göras genom att mäta en känd ljuskälla och bestämma överföringsfunktionen eller kalibreringskurvan .

Total utgångsbestrålning

För en sfär med radie r, reflektionskoefficient ρ och källflöde Φ är den initiala reflekterade irradiansen lika med:

$E=\rho {\frac {\Phi }{4\pi r^{2}}}\,$

Varje gång irradiansen reflekteras växer reflektionskoefficienten exponentiellt. Den resulterande ekvationen är

$E={\frac {\Phi }{4\pi r^{2}}}\,\rho (1+ \rho +\rho ^{2}+...)$

Eftersom ρ ≤ 1, konvergerar den geometriska serien och den totala utgående irradiansen är:

$E={\frac {\Phi }{4\pi r^{2}}}\,{\frac {\rho }{1-\rho }} \,$

Ansökningar

Förenklad princip för användningen av en integrerande sfär för att mäta transmittansen och reflektansen hos ett testprov

Integrerande sfärer används för en mängd olika optiska, fotometriska eller radiometriska mätningar. De används för att mäta det totala ljuset som utstrålas i alla riktningar från en lampa. En integrerande sfär kan användas för att skapa en ljuskälla med skenbar intensitet enhetlig över alla positioner inom dess cirkulära öppning, och oberoende av riktning förutom cosinusfunktionen som är inneboende i idealiskt diffusa strålningsytor ( Lambertianska ytor ). En integrerande sfär kan användas för att mäta den diffusa reflektansen av ytor, vilket ger ett medelvärde över alla belysnings- och observationsvinklar.

Det finns ett antal metoder för att mäta den absoluta reflektansen hos ett testobjekt monterat på en integrerande sfär. År 1916 publicerade EB Rosa och AH Taylor den första sådana metoden. Efterföljande arbete av AH Taylor, Frank A. Benford, CH Sharpe & WF Little, Enoch Karrer och Leonard Hanssen & Simon Kaplan utökade antalet unika metoder som mäter portmonterade testobjekt. Edwards et al., Korte & Schmidt och Van den Akker et al. utvecklat metoder som mäter centermonterade testobjekt.

Ljus som sprids av det inre av den integrerande sfären är jämnt fördelat över alla vinklar. Den integrerande sfären används vid optiska mätningar. Den totala effekten (flödet) för en ljuskälla kan mätas utan att felaktigheter orsakas av källans eller mätanordningens riktningsegenskaper. Reflektion och absorption av prover kan studeras. Sfären skapar en referensstrålningskälla som kan användas för att tillhandahålla en fotometrisk standard.

Eftersom allt ljus som faller in på ingångsporten samlas in, kan en detektor som är ansluten till en integrerande sfär noggrant mäta summan av allt omgivande ljus som faller in på en liten cirkulär öppning. Den totala effekten av en laserstråle kan mätas, fri från effekterna av strålform, infallsriktning och infallsposition, såväl som polarisation .

Kommersiell integrerande sfär . Denna speciella modell från Electro Optical Industries använder fyra separata lampor som kan specificeras för att uppnå den erforderliga spektraleffekten från ultraviolett till infrarött .

Material

De optiska egenskaperna hos sfärens foder påverkar i hög grad dess noggrannhet. Olika beläggningar måste användas vid synliga, infraröda och ultravioletta våglängder. Kraftfulla belysningskällor kan värma eller skada beläggningen, så en integrerande sfär kommer att klassas för en maximal nivå av infallande effekt. Olika beläggningsmaterial används. För ljus med synligt spektrum använde tidiga experimentörer en avlagring av magnesiumoxid , och bariumsulfat har också en användbar platt reflektans över det synliga spektrumet. Olika patenterade PTFE- föreningar används också för mätningar av synligt ljus. Findeponerat guld används för infraröda mätningar.

Ett viktigt krav på beläggningsmaterialet är frånvaron av fluorescens. Fluorescerande material absorberar kortvågigt ljus och återutsänder ljus vid längre våglängder. På grund av de många spridningarna är denna effekt mycket mer uttalad i en integrerande sfär än för material som normalt bestrålas.

Strukturera

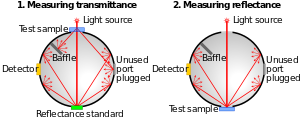
Teorin om den integrerande sfären antar en enhetlig inre yta med diffus reflektivitet som närmar sig 100 %. Öppningar där ljus kan komma ut eller komma in, som används för detektorer och källor, kallas normalt portar. Den totala arean för alla portar måste vara liten, mindre än cirka 5 % av sfärens yta, för att de teoretiska antagandena ska vara giltiga. Oanvända portar bör därför ha matchande pluggar, med insidan av pluggen belagd med samma material som resten av sfären.

Integrerande sfärer varierar i storlek från några centimeter i diameter upp till några meter i diameter. Mindre sfärer används vanligtvis för att sprida inkommande strålning, medan större sfärer används för att mäta integrerande egenskaper som ljusflödet från en lampa eller armaturer som sedan placeras inuti sfären.

Om det inkommande ljuset är inkoherent (snarare än en laserstråle), så fyller det vanligtvis källporten, och förhållandet mellan källportarea och detektorportarea är relevant.

Bafflar sätts normalt in i sfären för att blockera ljusets direkta väg från en källport till en detektorport, eftersom detta ljus kommer att ha ojämn fördelning.

Se även

Skulptur av en integrerande sfär. Beläget på campus vid Dresdens tekniska universitet

• Lamberts cosinus lag

externa länkar

• RP Photonics, Encyclopedia of Laser Physics and Technology , Integrering av sfärer
• Pike Technologies, Integrating Spheres – Introduktion och teori , Pike Technologies Application Note
• Newport, flänsmonterade integrerande sfärer
• Whitehead, Lorne A.; Mossman, Michele A. (2006). "Jack O'Lanterns och integrerande sfärer: Halloween Physics" . American Journal of Physics . 74 (6): 537–541. Bibcode : 2006AmJPh..74..537W . doi : 10.1119/1.2190687 .
•   Ducharme, Alfred; Daniels, Arnold; Grann, Eric; Boreman, Glenn (1997). "Design av en integrerande sfär som en enhetlig belysningskälla" . IEEE-transaktioner på utbildning . 40 (2): 131–134. Bibcode : 1997ITEdu..40..131D . doi : 10.1109/13.572326 . S2CID 61946451 .
• Peter Hiscocks, Integrating Sphere for Luminance Calibration , Rev 6, maj 2016
• Ci Systems, Integrating sfärintroduktion, mekanisk struktur, kalibrering och källor
• Elektro-optiska industrier, integrerande sfärer
• Statusen för den integrerande sfären i Kina