Informationsflaskhalsmetod

Informationsflaskhalsmetoden är en teknik inom informationsteori introducerad av Naftali Tishby , Fernando C. Pereira och William Bialek . Den är utformad för att hitta den bästa avvägningen mellan noggrannhet och komplexitet ( komprimering ) när man summerar (t.ex. klustring ) en slumpvariabel X , givet en gemensam sannolikhetsfördelning p(X,Y) mellan X och en observerad relevant variabel Y - och självbeskriven som att tillhandahålla "ett förvånansvärt rikt ramverk för att diskutera en mängd olika problem inom signalbehandling och inlärning" .

Tillämpningar inkluderar distributionskluster och dimensionsreduktion , och på senare tid har det föreslagits som en teoretisk grund för djupt lärande . Den generaliserade den klassiska uppfattningen om minimal tillräcklig statistik från parametrisk statistik till godtyckliga fördelningar, inte nödvändigtvis av exponentiell form. Den gör det genom att slappna av villkoret för att fånga en del av den ömsesidiga informationen med den relevanta variabeln Y .

Informationsflaskhalsen kan också ses som ett hastighetsförvrängningsproblem , med en distorsionsfunktion som mäter hur väl Y förutsägs från en komprimerad representation T jämfört med dess direkta förutsägelse från X . Denna tolkning tillhandahåller en allmän iterativ algoritm för att lösa informationsflaskhalsavvägningen och beräkna informationskurvan från fördelningen p(X,Y) .

Låt den komprimerade representationen ges av slumpvariabeln $T$ . Algoritmen minimerar följande funktionalitet med avseende på villkorlig fördelning $p(t|x)$ :

$\min _{p(t|x)}\,\,I(X;T)-\beta I (TACK),$

där $I(X;T)$ och $I(T;Y)$ är den ömsesidiga informationen för $X$ och $T$ , och av $T$ respektive $Y$ , och $\beta$ är en Lagrange-multiplikator .

Informationsteori om djupinlärning

Theory of Information Bottleneck används nyligen för att studera Deep Neural Networks (DNN). Betrakta $X$ respektive $Y$ som ingångs- och utgångsskikt för en DNN, och låt $T$ vara vilket dolt lager i nätverket som helst. Shwartz-Ziv och $I(T,Y)$ föreslog informationsflaskhalsen som uttrycker avvägningen mellan de ömsesidiga informationsmåtten $I(X,T)$ och . I detta fall kvantifierar $I(X,T)$ respektive $I(T,Y)$ mängden information som det dolda lagret innehåller om input och output. De förmodade att utbildningsprocessen för en DNN består av två separata faser; 1) en initial passningsfas i vilken $I(T,Y)$ ökar, och 2) en efterföljande kompressionsfas i vilken $I(X,T)$ minskar. Saxe et al. i motsatte sig påståendet från Shwartz-Ziv och Tishby, och angav att detta komprimeringsfenomen i DNN inte är heltäckande, och det beror på den särskilda aktiveringsfunktionen. I synnerhet hävdade de att komprimeringen inte sker med ReLu-aktiveringsfunktioner. Shwartz-Ziv och Tishby bestred dessa påståenden och hävdade att Saxe et al inte hade observerat komprimering på grund av svaga uppskattningar av den ömsesidiga informationen. Nyligen har Noshad et al. använde en hastighetsoptimal estimator av ömsesidig information för att utforska denna kontrovers, och observerade att den optimala hash-baserade estimatorn avslöjar komprimeringsfenomenet i ett bredare utbud av nätverk med ReLu- och maxpooling-aktiveringar. Å andra sidan har nyligen Goldfeld et al. har hävdat att den observerade kompressionen är ett resultat av geometriska, och inte av informationsteoretiska fenomen, en syn som har delats även i.

Gaussisk flaskhals

Den Gaussiska flaskhalsen, nämligen att tillämpa informationsflaskhalsmetoden på Gaussiska variabler, leder till lösningar relaterade till kanonisk korrelationsanalys . Antag att $X,Y\,$ tillsammans är multivariata nollmedelnormalvektorer med kovarianser $\Sigma _{XX},\,\,\Sigma _{YY}$ och $T\,$ är en komprimerad version av $X\,$ som måste bibehålla ett givet värde för ömsesidig information med $Y\,$ . Det kan visas att den optimala $T\,$ är en normalvektor som består av linjära kombinationer av elementen i $X,\,\,T=AX\,$ där matris $A\,$ har ortogonala rader.

Projektionsmatrisen $A\,$ innehåller faktiskt $M\,$ rader valda från de viktade vänstra egenvektorerna för singularvärdesuppdelningen av matrisen (vanligen asymmetrisk)

$\Omega =\Sigma _{X|Y}\Sigma _{XX}^{-1}=I-\Sigma _{XY}\Sigma _{YY}^{-1}\Sigma _{XY }^{T}\Sigma _{XX}^{-1}.\,$

Definiera singularvärdesuppdelningen

$\Omega =U\Lambda V^{T}{\text{ med }}\Lambda =\operatörsnamn {Diag} {\big (}\lambda _{1}\leq \lambda _{2}\cdots \lambda _{N}{\big )}\,$

och de kritiska värdena

$\beta _{i}^{C}{\underset {\lambda _{i}<1}{=}}(1-\lambda _{i})^{-1}.\,$

då ges antalet $M\,$ för aktiva egenvektorer i projektionen, eller approximationsordningen, av

$\beta _{M-1}^{C}<\beta \leq \beta _{M}^{C}$

Och vi får äntligen

$A=[w_{1}U_{1},\dots ,w_{M}U_{M}]^{T}$

I vilken vikterna ges av

$w_{i}={\sqrt {(\beta (1-\lambda _{i})/\lambda _{i}r_{ i}}}$

där $r_{i}=U_{i}^{T}\Sigma _{XX}U_{i}.\,$

Att tillämpa den Gaussiska informationsflaskhalsen på tidsserier (processer), ger lösningar relaterade till optimal prediktiv kodning. Denna procedur är formellt likvärdig med linjär Slow Feature Analysis.

Optimala tidsstrukturer i linjära dynamiska system kan avslöjas i den så kallade tidigare-framtidsinformationsflaskhalsen, en tillämpning av flaskhalsmetoden på icke-Gaussisk samplade data. Konceptet, som behandlats av Creutzig, Tishby et al., är inte utan komplikationer eftersom två oberoende faser utgörs av övningen: för det första uppskattning av de okända modersannolikhetstätheterna från vilka datasamplen är dragna och för det andra användningen av dessa tätheter inom den informationsteoretiska ramen för flaskhalsen.

Densitetsuppskattning

Huvudartikel: Densitetsuppskattning

Eftersom flaskhalsmetoden är inramad i probabilistiska snarare än statistiska termer, måste den underliggande sannolikhetstätheten vid provpunkterna $X={x_{i}}\,$ uppskattas. Detta är ett välkänt problem med flera lösningar som beskrivs av Silverman . I den föreliggande metoden hittas sannolikheter för gemensamma prov genom användning av en Markov-övergångsmatrismetod och detta har viss matematisk synergi med själva flaskhalsmetoden.

Det godtyckligt ökande avståndsmåttet $f\,$ mellan alla sampelpar och avståndsmatrisen är $d_{i,j}=f{\Big (}{\Big |}x_{i}-x_{j}{\Big |}{\Big )}$ . Övergångssannolikheter mellan sampelparen $P_{i,j}=\exp(-\lambda d_{i,j})\,$ för vissa $\lambda >0\,$ måste beräknas. Behandling av sampel som tillstånd och en normaliserad version av $P\,$ som en Markov-tillståndsövergångssannolikhetsmatris, vektorn av sannolikheter för 'tillstånden' efter $t\,$ steg, betingad av den initiala tillstånd $p(0)\,$ , är $p(t)=P^{t}p(0)\,$ . Jämviktssannolikhetsvektorn $p(\infty )\,$ given, på vanligt sätt, av den dominanta egenvektorn för matrisen $P\,$ som är oberoende av den initialiserande vektorn $p(0)\,$ . Denna Markov-övergångsmetod fastställer en sannolikhet vid provpunkterna som påstås vara proportionell mot sannolikheternas densiteter där.

Andra tolkningar av användningen av egenvärdena för avståndsmatris $d\,$ diskuteras i Silverman's Density Estimation for Statistics and Data Analysis .

Kluster

I följande mjuka klustringsexempel innehåller referensvektorn $Y\,$ exempelkategorier och den gemensamma sannolikheten $p(X,Y)\,$ antas vara känd. Ett mjukt kluster $c_{k}\,$ definieras av dess sannolikhetsfördelning över datasamplen $x_{i}:\,\,\, p(c_{k}|x_{i})$ . Tishby et al. presenterade följande iterativa uppsättning ekvationer för att bestämma klustren som i slutändan är en generalisering av Blahut-Arimoto-algoritmen, utvecklad inom hastighetsförvrängningsteorin . Tillämpningen av denna typ av algoritm i neurala nätverk verkar ha sitt ursprung i entropiargument som uppstår vid tillämpningen av Gibbs-distributioner vid deterministisk glödgning.

${\begin{cases}p(c|x) =Kp(c)\exp {\Big (}-\beta \,D^{KL}{\Big [}p(y|x)\,||\,p(y|c){\Big ]} {\Big )}\\p(y|c)=\textstil \sum _{x}p(y|x)p(c|x)p(x){\big /}p(c)\\p (c)=\textstil \sum _{x}p(c|x)p(x)\\\end{case}}$

Funktionen för varje rad i iterationen expanderar som

Rad 1: Detta är en matrisvärderad uppsättning villkorliga sannolikheter

${\ displaystyle A_{i,j}=p(c_{i}|x_{j})=Kp(c_{i})\exp {\Big (}-\beta \,D^{KL}{\Big [}p (y|x_{j})\,||\,p(y|c_{i}){\Big ]}{\Big )}}$

Kullback –Leibler-divergensen $D^{KL}\,$ mellan ${\displaystyle Y\,}-$ vektorerna som genereras av exempeldatan $x\,$ och de som genereras av dess reducerade information proxy $c\,$ används för att bedöma den komprimerade vektorns trohet med avseende på referensdata (eller kategoriska) data $Y\,$ i enlighet med den grundläggande flaskhalsekvationen. $D^{KL}(a||b)\,$ är Kullback–Leibler-divergensen mellan distributionerna $a,b\,$

$D^{KL}(a||b)=\summa _{ i}p(a_{i})\log {\Big (}{\frac {p(a_{i})}{p(b_{i})}}{\Big )}$

och $K\,$ är en skalär normalisering. Viktningen av avståndets negativa exponent innebär att tidigare klustersannolikheter nedviktas i rad 1 när Kullback–Leibler-divergensen är stor, så framgångsrika kluster växer i sannolikhet medan misslyckade sönderfaller.

Rad 2: Andra matrisvärderade uppsättningen villkorade sannolikheter. Per definition

${\begin{aligned}p(y_{i}|c_{ k})&=\summa _{j}p(y_{i}|x_{j})p(x_{j}|c_{k})\\&=\summa _{j}p(y_{i }|x_{j})p(x_{j},c_{k}){\big /}p(c_{k})\\&=\summa _{j}p(y_{i}|x_{ j})p(c_{k}|x_{j})p(x_{j}){\big /}p(c_{k})\\\end{aligned}}$

där Bayes-identiteterna $p(a,b)=p(a|b)p( b)=p(b|a)p(a)\,$ används.

Rad 3: denna linje hittar marginalfördelningen av klustren $c\,$

${\begin{aligned}p(c_{i})&= \sum _{j}p(c_{i},x_{j})&=\summa _{j}p(c_{i}|x_{j})p(x_{j})\end{aligned} }$

Detta är ett standardresultat.

Ytterligare indata till algoritmen är marginalsampelfördelningen $p(x)\,$ som redan har bestämts av den dominanta egenvektorn för $P\,$ och den matrisvärderade Kullback–Leibler-divergensen fungera

$D_{i,j}^{KL}=D^{KL}{\Big [}p(y|x_{j})\,||\,p( y|c_{i}){\Big ]}{\Big )}$

härledd från urvalsavstånden och övergångssannolikheter.

Matrisen $p(y_{i}|c_{j})\,$ kan initieras slumpmässigt eller med en rimlig gissning, medan matrisen ${\ displaystyle p(c_{i}|x_{j})\,}$ behöver inga tidigare värden. Även om algoritmen konvergerar kan det finnas flera minima som skulle behöva lösas.

Definiera beslutskonturer

För att kategorisera ett nytt prov $x'\,$ utanför träningsuppsättningen $X\,$ , hittar det föregående distansmåttet övergångssannolikheterna mellan $x'\,$ och alla sampel i $X:\,\,$ , ${\ displaystyle {\tilde {p}}(x_{i})=p(x_{i}|x')=\mathrm {K} \exp {\Big (}-\lambda f{\big (}{\Big) |}x_{i}-x'{\Big |}{\big )}{\Big )}}$ med $\mathrm {K} \,$ en normalisering. För det andra tillämpa de två sista raderna i 3-radsalgoritmen för att få kluster- och villkorskategorisannolikheter.

${\begin{aligned}&{\tilde {p}}(c_{i}) =p(c_{i}|x')=\summa _{j}p(c_{i}|x_{j})p(x_{j}|x')=\summa _{j}p(c_ {i}|x_{j}){\tilde {p}}(x_{j})\\&p(y_{i}|c_{j})=\summa _{k}p(y_{i}| x_{k})p(c_{j}|x_{k})p(x_{k}|x')/p(c_{j}|x')=\summa _{k}p(y_{i }|x_{k})p(c_{j}|x_{k}){\tilde {p}}(x_{k})/{\tilde {p}}(c_{j})\\\end {Justerat}}$

Till sist

$p( y_{i}|x')=\summa _{j}p(y_{i}|c_{j})p(c_{j}|x'))=\summa _{j}p(y_{i }|c_{j}){\tilde {p}}(c_{j})\,$

Parametern $\beta \,$ måste hållas under noggrann övervakning eftersom, när den ökas från noll, ökar antalet funktioner, i kategorins sannolikhetsutrymme, i fokus vid vissa kritiska trösklar.

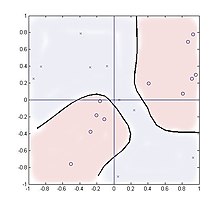
Ett exempel

Följande fall undersöker klustring i en multiplikator med fyra kvadranter med slumpmässiga ingångar $u,v\,$ och två kategorier av utdata, $\pm 1\,$ , genererad av $y=\operatörsnamn {tecken} (uv)\,$ . Denna funktion har två rumsligt separerade kluster för varje kategori och visar på så sätt att metoden kan hantera sådana distributioner.

20 prover tas, jämnt fördelade på kvadraten $[-1,1]^{2}\,$ . Antalet kluster som används utöver antalet kategorier, två i detta fall, har liten effekt på prestandan och resultaten visas för två kluster med parametrarna $\lambda =3,\,\beta =2,5$ .

Avståndsfunktionen ${\displaystyle d_{i,j}={\Big |}x_{i}-x_{j}{\Big |}^{2}} där$ x $\displaystyle x_{i}=(u_{i},v_{i})^{T}\,}$ medan den villkorliga fördelningen $p(y|x)\,$ är en 2 × 20 matris

${\begin {aligned}&Pr(y_{i}=1)=1{\text{ if }}\operatörsnamn {tecken} (u_{i}v_{i})=1\,\\&Pr(y_{i}=- 1)=1{\text{ if }}\operatörsnamn {tecken} (u_{i}v_{i})=-1\,\end{aligned}}$

och noll någon annanstans.

Summeringen i rad 2 innehåller endast två värden som representerar träningsvärdena +1 eller −1, men fungerar ändå bra. Figuren visar placeringen av de tjugo proverna där '0' representerar Y = 1 och 'x' representerar Y = −1. Konturen vid enhetssannolikhetsförhållandet visas,

$L={\frac {\Pr(1)}{\Pr(-1)}}=1$

som ett nytt exempel skannas ${\displaystyle x'\,} över kvadraten.$ Teoretiskt sett bör konturen vara i linje med koordinaterna $u=0\,$ och ${\displaystyle v=0\,},$ men för så små provnummer har de istället följt sampelpunkternas falska klustringar.

Beslutskonturer

Analogier av neurala nätverk/suddig logik

Denna algoritm är något analog med ett neuralt nätverk med ett enda dolt lager. De interna noderna representeras av klustren $c_{j}\,$ och det första och andra lagret av nätverksvikter är de villkorliga sannolikheterna $p(c_{j} |x_{i})\,$ respektive $p(y_{k}|c_{j})\,$ . Men till skillnad från ett standardneuralt nätverk, bygger algoritmen helt på sannolikheter som indata snarare än själva provvärdena, medan interna och utgående värden alla är villkorade sannolikhetstäthetsfördelningar. Icke-linjära funktioner är inkapslade i avståndsmetriska $f(.)\,$ (eller influensfunktioner/radialbasfunktioner ) och övergångssannolikheter istället för sigmoidfunktioner.

Blahut-Arimoto treradiga algoritm konvergerar snabbt, ofta i tiotals iterationer, och genom att variera ${\displaystyle \beta \,} ,$ λ $\displaystyle \lambda \,}$ och $f\,$ och kardinalitet av klustren, kan olika nivåer av fokus på funktioner uppnås.

Den statistiska mjuka klustringsdefinitionen ${\displaystyle p(c_{i}|x_{j})\,} har viss överlappning med$ verbala fuzzy medlemskapskonceptet för fuzzy logic .

Tillägg

En intressant förlängning är fallet med informationsflaskhals med sidoinformation. Här maximeras information om en målvariabel och minimeras om en annan, och lär sig en representation som är informativ om utvalda aspekter av data. Formellt

$\min _{p(t|x)}\,\ ,I(X;T)-\beta ^{+}I(T;Y^{+})+\beta ^{-}I(T;Y^{-})$

Bibliografi

• Weiss, Y. (1999), "Segmentation using eigenvectors: a unifying view", Proceedings IEEE International Conference on Computer Vision (PDF) , s. 975–982
• P. Harremoës och N. Tishby "The Information Bottleneck Revisited or How to Choose a Good Distortion Measure". I handlingar från International Symposium on Information Theory (ISIT) 2007