Influenslinje

Figur 1: (a) Denna enkla stödda balk visas med en enhetslast placerad ett avstånd x från den vänstra änden. Dess influenslinjer för fyra olika funktioner: (b) reaktionen vid det vänstra stödet (betecknat A), (c) reaktionen vid det högra stödet (betecknat C), (d) en för skjuvning vid en punkt B längs balken, och (e) en för ögonblicket också vid punkt B.

Figur 2: Förändringen i böjmoment i en statiskt bestämd stråle när en enhetskraft rör sig från ena änden till den andra. Böjmomentdiagrammet och påverkanslinjen för böjmoment i mitten av det vänstra spannet, B, visas.

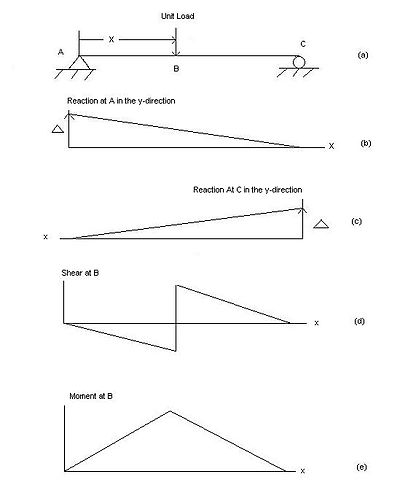
Inom tekniken visar en influenslinje en graf över variationen av en funktion (såsom skjuvningen, momentet etc. som känns i en konstruktionsdel) vid en specifik punkt på en balk eller fackverk orsakad av en enhetslast placerad vid någon punkt längs strukturen. Vanliga funktioner som studeras med influenslinjer inkluderar reaktioner (krafter som strukturens stöd måste anbringa för att strukturen ska förbli statisk), skjuvning , moment och deformation (Deformation). Influenslinjer är viktiga vid utformning av balkar och takstolar som används i broar , kranskenor, transportband , golvbalkar och andra strukturer där laster kommer att röra sig längs deras spännvidd. Influenslinjerna visar var en belastning kommer att skapa maximal effekt för någon av de studerade funktionerna.

Influenslinjer är både skalära och additiva . Detta innebär att de kan användas även när belastningen som kommer att appliceras inte är en enhetsbelastning eller om det finns flera belastningar. För att hitta effekten av en icke-enhetsbelastning på en konstruktion multipliceras ordinatresultaten som erhålls av påverkanslinjen med storleken på den faktiska belastningen som ska appliceras. Hela påverkanslinjen kan skalas, eller bara de maximala och minimala effekterna som upplevs längs linjen. Det skalade maximum och minimum är de kritiska magnituder som måste utformas för i balken eller fackverket.

I de fall där flera belastningar kan förekomma, kan påverkanslinjer för de enskilda belastningarna läggas samman för att erhålla den totala effekt som konstruktionen upplever vid en given punkt. När man lägger ihop påverkanslinjerna är det nödvändigt att inkludera lämpliga förskjutningar på grund av lastavståndet över strukturen. Till exempel appliceras en lastbilslast på strukturen. Bakaxel, B, är tre fot bakom framaxeln, A, då måste effekten av A vid x fot längs strukturen läggas till effekten av B vid ( x – 3) fot längs strukturen – inte effekten av B vid x fot längs strukturen.

Många laster är fördelade snarare än koncentrerade. Influenslinjer kan användas med antingen koncentrerade eller fördelade belastningar. För en koncentrerad (eller punkt) last flyttas en enhetspunktlast längs strukturen. För en fördelad last med en given bredd flyttas en enhetsfördelad last med samma bredd längs strukturen, varvid man noterar att när lasten närmar sig ändarna och flyttar sig från strukturen bärs endast en del av den totala lasten av strukturen. Effekten av den fördelade enhetslasten kan också erhållas genom att integrera punktlastens påverkanslinje över motsvarande längd av konstruktionerna.

Påverkanslinjerna för bestämda strukturer blir en mekanism medan påverkanslinjerna för obestämda strukturer bara blir bestämda.

Demonstration från Bettis teorem

Influenslinjer är baserade på Bettis sats . Därifrån, betrakta två externa kraftsystem, $F_{i}^{P}$ och $F_{i}^{Q}$ , vart och ett associerat med ett förskjutningsfält vars förskjutningar mätt i kraftens appliceringspunkt representeras av $d_{i}^{P}$ och $d_{i}^{Q}$ .

Tänk på att ${\displaystyle F_{i}^{P}}-$ systemet representerar faktiska krafter som appliceras på strukturen, som är i jämvikt. Tänk på att ${\displaystyle F_{i}^{Q}}-$ systemet bildas av en enda kraft, $F^{Q}$ . Förskjutningsfältet $d_{i}^{Q}$ som är associerat med denna forcerade definieras genom att släppa de strukturella begränsningarna som verkar på den punkt där $F^{Q}$ tillämpas och införa en relativ enhetsförskjutning som är kinematiskt tillåten i negativ riktning, representerad som $d_{1}^{Q}=-1$ . Från Bettis teorem får vi följande resultat:

$-F_{1}^{P}+\ summa _{i=2}^{n}F_{i}^{P}d_{i}^{Q}=F^{Q}\ gånger 0\iff F_{1}^{P}=\summa _ {i=2}^{n}F_{i}^{P}d_{i}^{Q}$

Begrepp

Vid utformning av en balk eller fackverk är det nödvändigt att designa för de scenarier som orsakar maximala förväntade reaktioner, skjuvningar och moment i strukturelementen för att säkerställa att ingen del går sönder under strukturens livslängd. När man hanterar döda laster (laster som aldrig rör sig, såsom vikten av själva strukturen) är detta relativt enkelt eftersom lasterna är lätta att förutse och planera för. För levande laster (alla laster som rör sig under strukturens livslängd, såsom möbler och människor), blir det mycket svårare att förutsäga var lasterna kommer att vara eller hur koncentrerade eller fördelade de kommer att vara under hela strukturens livslängd.

Influenslinjer visar en balks eller fackverks respons när en enhetslast rör sig över den. Influenslinjen hjälper designers att hitta var de ska placera en levande last för att beräkna det maximala resultatet för var och en av följande funktioner: reaktion, skjuvning eller moment. Konstruktören kan sedan skala påverkanslinjen med den största förväntade belastningen för att beräkna den maximala responsen för varje funktion för vilken balken eller fackverket måste konstrueras. Influenslinjer kan också användas för att hitta svaren för andra funktioner (som avböjning eller axiell kraft) på den applicerade enhetsbelastningen, men dessa användningar av influenslinjer är mindre vanliga.

Metoder för att konstruera påverkanslinjer

Det finns tre metoder som används för att konstruera påverkanslinjen. Den första är att tabulera påverkansvärdena för flera punkter längs strukturen och sedan använda dessa punkter för att skapa påverkanslinjen. Den andra är att bestämma influenslinjeekvationerna som gäller för strukturen, och därigenom lösa för alla punkter längs påverkanslinjen i termer av x , där x är antalet fot från strukturens början till den punkt där enhetsbelastningen tillämpas. Den tredje metoden kallas Müller-Breslaus princip . Det skapar en kvalitativ påverkanslinje. Denna influenslinje kommer fortfarande att ge konstruktören en korrekt uppfattning om var enhetsbelastningen kommer att producera det största svaret av en funktion vid den punkt som studeras, men den kan inte användas direkt för att beräkna vilken storlek det kommer att vara, medan påverkan linjer som produceras av de två första metoderna kan.

Tabulera värden

För att tabellera påverkansvärdena med avseende på någon punkt A på konstruktionen måste en enhetslast placeras på olika punkter längs konstruktionen. Statik används för att beräkna vad värdet på funktionen (reaktion, skjuvning eller moment) är vid punkt A. Typiskt ses en reaktion uppåt som positiv. Skjuvning och moment ges positiva eller negativa värden enligt samma konventioner som används för skjuvnings- och momentdiagram .

RC Hibbeler säger, i sin bok Structural Analysis , "Alla statiskt bestämda strålar kommer att ha inverkanslinjer som består av raka linjesegment." Därför är det möjligt att minimera antalet beräkningar genom att känna igen de punkter som kommer att orsaka en förändring i lutningen på påverkanslinjen och endast beräkna värdena vid dessa punkter. Böjningslinjens lutning kan ändras vid stöd, mittspann och leder.

En påverkanslinje för en given funktion, såsom en reaktion, axiell kraft, skjuvkraft eller böjmoment, är en graf som visar variationen av den funktionen vid en given punkt på en struktur på grund av appliceringen av en enhetslast vid någon punkt på strukturen.

En influenslinje för en funktion skiljer sig från ett skjuv-, axial- eller böjmomentdiagram. Influenslinjer kan genereras genom att oberoende applicera en enhetslast på flera punkter på en struktur och bestämma värdet på funktionen på grund av denna last, dvs skjuvning, axiell och moment på önskad plats. De beräknade värdena för varje funktion plottas sedan där belastningen applicerades och kopplas sedan samman för att generera påverkanslinjen för funktionen.

När påverkansvärdena har tabellerats kan påverkanslinjen för funktionen i punkt A ritas i termer av x . Först måste de tabellerade värdena lokaliseras. För sektionerna mellan de tabellerade punkterna krävs interpolering. Därför kan raka linjer dras för att koppla ihop punkterna. När detta är gjort är inflytandelinjen klar.

Influenslinjeekvationer

Det är möjligt att skapa ekvationer som definierar påverkanslinjen över hela spännvidden av en struktur. Detta görs genom att lösa reaktionen, skjuvningen eller momentet i punkten A som orsakas av en enhetslast placerad på x fot längs strukturen istället för ett specifikt avstånd. Denna metod liknar metoden med tabellerade värden, men istället för att erhålla en numerisk lösning är resultatet en ekvation i termer av x .

Det är viktigt att förstå var påverkanslinjens lutning ändras för denna metod eftersom influenslinjeekvationen kommer att ändras för varje linjär sektion av påverkanslinjen. Därför är den fullständiga ekvationen en bitvis linjär funktion med en separat influenslinjeekvation för varje linjär sektion av påverkanslinjen.

Müller-Breslaus princip

Enligt www.public.iastate.edu, " Müller-Breslau-principen kan användas för att rita kvalitativa inflytandelinjer, som är direkt proportionella mot den faktiska påverkanslinjen." Istället för att flytta en enhetslast längs en balk, hittar Müller-Breslau-principen den avböjda formen på strålen som orsakas av att man först släpper strålen vid den punkt som studeras och sedan tillämpar funktionen (reaktion, skjuvning eller moment) som studeras på den punkten. Principen säger att influenslinjen för en funktion kommer att ha en skalad form som är densamma som strålens avböjda form när strålen påverkas av funktionen.

För att förstå hur strålen avböjs under funktionen är det nödvändigt att ta bort strålens förmåga att motstå funktionen. Nedan finns förklaringar av hur man hittar påverkanslinjerna för en enkelt stödd, stel balk (som den som visas i figur 1).

• Vid bestämning av reaktionen som orsakas vid ett stöd, ersätts stödet med en rulle, som inte kan motstå en vertikal reaktion. Sedan appliceras en uppåtgående (positiv) reaktion till den punkt där stödet var. Eftersom stödet har tagits bort kommer balken att rotera uppåt, och eftersom balken är stel kommer den att skapa en triangel med spetsen vid det andra stödet. Om balken sträcker sig bortom det andra stödet som en konsol, kommer en liknande triangel att bildas under konsolens position. Detta innebär att reaktionens påverkanslinje kommer att vara en rak, lutande linje med värdet noll vid platsen för det andra stödet.

• Vid bestämning av skjuvningen som orsakas vid någon punkt B längs balken, måste balken skäras och en rullstyrning (som kan motstå moment men inte skjuvning) måste sättas in i punkt B. Sedan, genom att applicera en positiv skjuvning på den punkt, kan det ses att den vänstra sidan kommer att rotera nedåt, men den högra sidan kommer att rotera uppåt. Detta skapar en diskontinuerlig påverkanslinje som når noll vid stöden och vars lutning är lika stor på båda sidor om diskontinuiteten. Om punkt B är vid ett stöd, kommer avböjningen mellan punkt B och eventuella andra stöd fortfarande att skapa en triangel, men om balken är fribärande kommer hela den fribärande sidan att röra sig uppåt eller nedåt och skapa en rektangel.

• När man bestämmer det moment som orsakas av någon punkt B längs balken, kommer ett gångjärn att placeras vid punkt B, vilket släpper det till moment men motstår skjuvning. När sedan ett positivt moment placeras vid punkt B, kommer båda sidor av strålen att rotera uppåt. Detta kommer att skapa en kontinuerlig påverkanslinje, men lutningarna kommer att vara lika och motsatta på vardera sidan av gångjärnet vid punkt B. Eftersom balken helt enkelt stöds kan dess ändstöd (stift) inte motstå moment; därför kan det observeras att stöden aldrig kommer att uppleva moment i en statisk situation oavsett var lasten placeras.

Müller-Breslau-principen kan bara producera kvalitativa påverkanslinjer. Detta innebär att ingenjörer kan använda den för att bestämma var en belastning ska placeras för att få maximalt av en funktion, men storleken på detta maximum kan inte beräknas från påverkanslinjen. Istället måste ingenjören använda statik för att lösa funktionsvärdet i det belastningsfallet.

Alternativa lastfall

Flera laster

Det enklaste belastningsfallet är en enda punktbelastning, men påverkanslinjer kan också användas för att bestämma svar på grund av flera belastningar och fördelade belastningar. Ibland är det känt att flera belastningar kommer att inträffa på ett fast avstånd från varandra. Till exempel, på en bro skapar hjulen på bilar eller lastbilar punktlaster som verkar på relativt standardavstånd.

För att beräkna responsen av en funktion på alla dessa punktbelastningar med hjälp av en influenslinje kan resultaten som hittas med påverkanslinjen skalas för varje last, och sedan kan de skalade magnituderna summeras för att hitta den totala responsen som strukturen måste tåla. Punktlasterna kan själva ha olika storlek, men även om de anbringar samma kraft på strukturen kommer det att vara nödvändigt att skala dem separat eftersom de verkar på olika avstånd längs strukturen. Till exempel, om en bils hjul är 10 fot från varandra, då när den första uppsättningen är 13 fot på bron, kommer den andra uppsättningen bara att vara 3 fot på bron. Om den första uppsättningen hjul är 7 fot på bron, har den andra uppsättningen ännu inte nått bron, och därför är det bara den första uppsättningen som belastar bron.

Dessutom, om, mellan två laster, en av lasterna är tyngre, måste lasterna undersökas i båda lastordningarna (den större lasten till höger och den större lasten till vänster) för att säkerställa att den maximala lasten hittas. Om det finns tre eller fler belastningar ökar antalet fall som ska undersökas.

Fördelade belastningar

Många laster fungerar inte som punktlaster utan fungerar över en längre längd eller area som fördelade laster. Till exempel kommer en traktor med kontinuerliga spår att applicera en belastning fördelad över längden av varje spår.

För att hitta effekten av en fördelad last kan konstruktören integrera en influenslinje, hittad med hjälp av en punktlast, över det påverkade avståndet av strukturen. Till exempel, om ett tre fot långt spår verkar mellan 5 fot och 8 fot längs en balk, måste influenslinjen för den strålen integreras mellan 5 och 8 fot. Integreringen av influenslinjen ger den effekt som skulle märkas om den fördelade lasten hade en enhetsstorlek. Därför måste konstruktören efter integrering fortfarande skala resultaten för att få den faktiska effekten av den fördelade lasten.

Obestämda strukturer

Medan påverkanslinjerna för statiskt bestämda strukturer (som nämnts ovan) är uppbyggda av raka linjesegment, är detsamma inte sant för obestämda strukturer. Obestämda strukturer anses inte vara stela; därför kommer påverkanslinjerna som ritas för dem inte att vara raka linjer utan snarare kurvor. Metoderna ovan kan fortfarande användas för att bestämma inverkanslinjerna för strukturen, men arbetet blir mycket mer komplext då själva balkens egenskaper måste beaktas.

Se även

• Stråle
• Skjuvning och momentdiagram
• Döda och levande laster
• Müller-Breslaus princip