Hypotrochoid

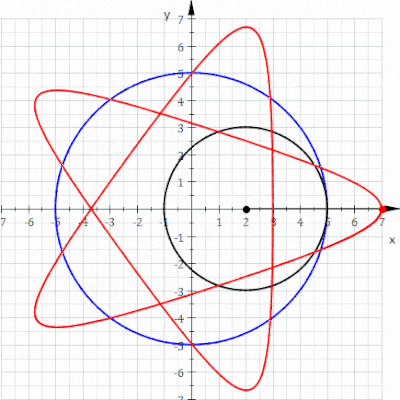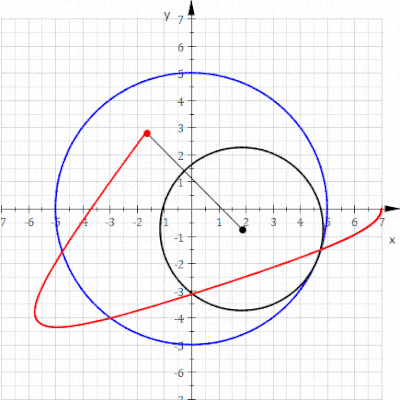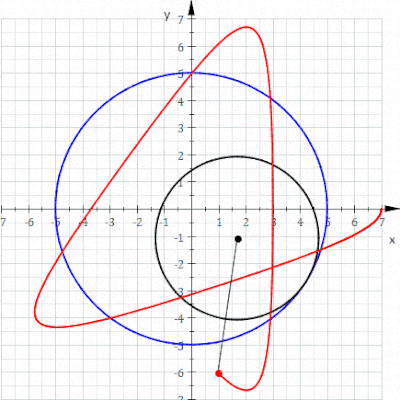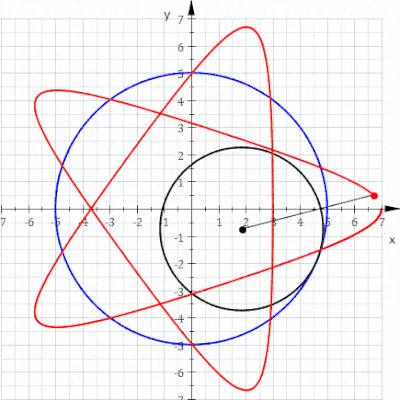
Den röda kurvan är en hypotrochoid ritad när den mindre svarta cirkeln rullar runt inuti den större blå cirkeln (parametrarna är

R = 5, r = 3, d = 5

).

I geometri är en hypotrochoid en roulette spårad av en punkt fäst vid en cirkel med radie $r$ som rullar runt insidan av en fast cirkel med radie $R$ , där punkten är ett avstånd $d$ från centrum av den inre cirkeln.

De parametriska ekvationerna för en hypotrokoid är:

{\ displaystyle {\begin{aligned}&x(\theta )=(Rr)\cos \theta +d\cos \left({Rr \over r}\theta \right)\\&y(\theta )=(Rr)\ sin \theta -d\sin \left({Rr \over r}\theta \right)\end{aligned}}}

där $θ$ är vinkeln som bildas av den rullande cirkelns horisontella och mittpunkt (detta är inte polära ekvationer eftersom $θ$ inte är den polära vinkeln). När den mäts i radian $θ$ värden från 0 till $2\pi \times {\tfrac {\operatörsnamn {LCM} (r,R)}{R}}$ (där $LCM$ är minsta gemensamma multipel ).

Specialfall inkluderar hypocykloiden med d $= r och$ ellipsen med R $= 2 r$ och $d \neq r$ . Ellipsens excentricitet är

e={\frac {2{\sqrt {d/r}}}{1+(d/r)}}

blir 1 när $d=r$ (se Tusi-paret ).

Ellipsen ( ritad i rött) kan uttryckas som ett specialfall av hypotrochoiden, med

R = 2 r

( Tusi couple ); här är

R = 10, r = 5, d = 1

.

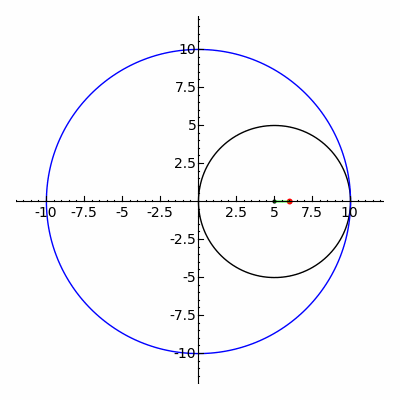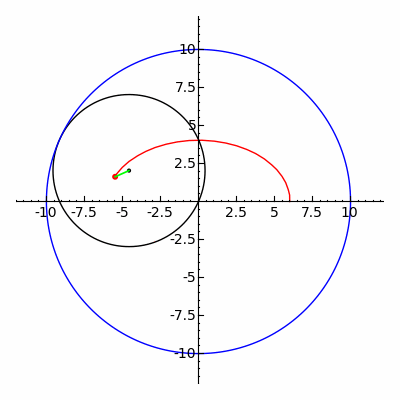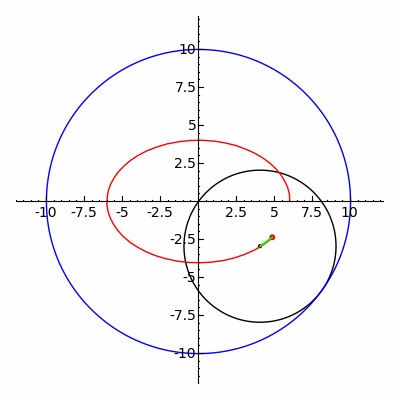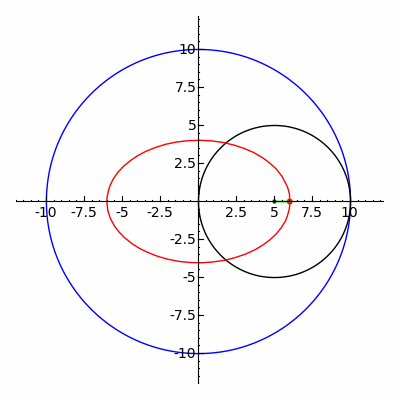
Den klassiska Spirograph -leksaken spårar ut hypotrochoid- och epitrochoidkurvor .

Hypotrochoider beskriver stödet för egenvärdena för vissa slumpmässiga matriser med cykliska korrelationer

Se även

^ J. Dennis Lawrence (1972). En katalog med speciella plankurvor . Dover Publikationer. s. 165–168 . ISBN 0-486-60288-5 .
^ Grå, Alfred . Modern differentialgeometri av kurvor och ytor med Mathematica ( andra upplagan). CRC Tryck. sid. 906. ISBN 9780849371646 .
^ Aceituno, Pau Vilimelis; Rogers, Tim; Schomerus, Henning (2019-07-16). "Universell hypotrochoid lag för slumpmässiga matriser med cykliska korrelationer" . Fysisk granskning E . 100 (1): 010302. doi : 10.1103/PhysRevE.100.010302 .

externa länkar

Weisstein, Eric W. "Hypotrochoid" . MathWorld .
Flash-animering av Hypocycloid
Hypotrochoid från Visual Dictionary of Special Plane Curves, Xah Lee
Interaktiv hypotrochoid-animation
O'Connor, John J.; Robertson, Edmund F. , "Hypotrochoid" , MacTutor History of Mathematics arkiv , University of St Andrews

[1] J. Dennis Lawrence (1972). En katalog med speciella plankurvor . Dover Publikationer. s. 165–168 . ISBN 0-486-60288-5 .

[2] Grå, Alfred . Modern differentialgeometri av kurvor och ytor med Mathematica ( andra upplagan). CRC Tryck. sid. 906. ISBN 9780849371646 .

[3] Aceituno, Pau Vilimelis; Rogers, Tim; Schomerus, Henning (2019-07-16). "Universell hypotrochoid lag för slumpmässiga matriser med cykliska korrelationer" . Fysisk granskning E . 100 (1): 010302. doi : 10.1103/PhysRevE.100.010302 .