Cyklogon

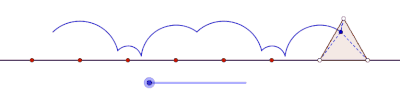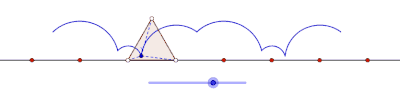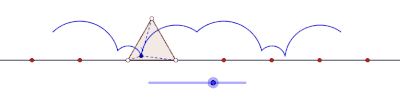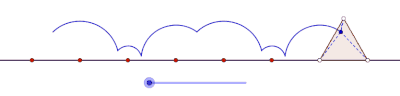
Inom geometrin är en cyklogon kurvan som spåras av en spets av en polygon som rullar utan att glida längs en rät linje . Det finns inga begränsningar för polygonens natur. Det kan vara en vanlig polygon som en liksidig triangel eller en kvadrat . Polygonen behöver inte ens vara konvex : den kan till och med vara en stjärnformad polygon . Mer generellt har kurvorna som spåras av andra punkter än hörn också beaktats. I sådana fall skulle det antas att spårningspunkten är stelt fäst vid polygonen. Om spårningspunkten är belägen utanför polygonen kallas kurvan en prolatcyklon , och om den ligger inuti polygonen kallas den för en curtate-cyklogon .

I gränsen, när antalet sidor ökar till oändlighet, blir cyklonen en cykloid .

Cyklogonen har en intressant egenskap vad gäller sitt område. Låt $A$ beteckna arean av området ovanför linjen och under en av bågarna, låt $P$ beteckna arean av den rullande polygonen och låt $C$ beteckna arean av skivan som omger polygonen. För varje cyklon som genereras av en vanlig polygon,

A=P+2C.\,

Exempel

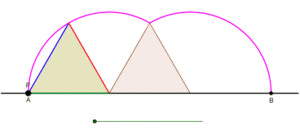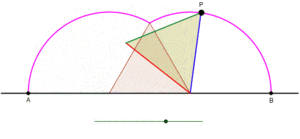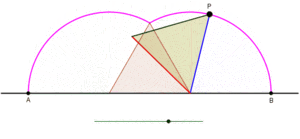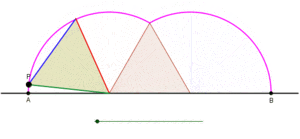
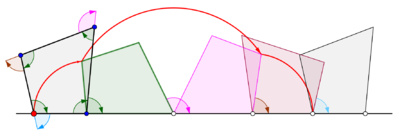
Cyklogoner genererade av en liksidig triangel och en kvadrat

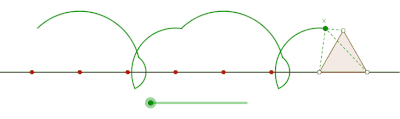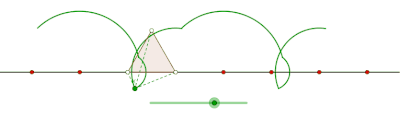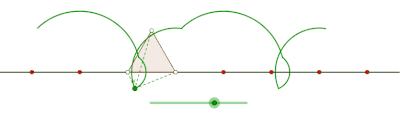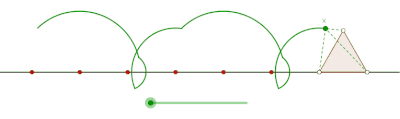
Animation som visar genereringen av en båge av en cyklon av en liksidig triangel när triangeln rullar över en rak linje utan att glida.	Animation som visar genereringen av en båge av en cyklon av en kvadrat när kvadraten rullar över en rak linje utan att glida.

Prolatcyklon genererad av en liksidig triangel

Animation som visar spårningen av en prolatcyklon när en liksidig triangel rullar över en rak linje utan att hoppa över. Spårningspunkten X är utanför triangelns skiva.

Curtate cyklon som genereras av en liksidig triangel

Animation som visar spårningen av en kort cyklon när en liksidig triangel rullar över en rak linje utan att hoppa över. Spårningspunkten Y är inuti triangelns skiva.

Cyklogoner genererade av fyrhörningar

Cyklogon genererad av en konvex fyrhörning

Cyklogon genererad av en icke-konvex fyrhörning

Cyklogon genererad av en stjärnliknande fyrhörning

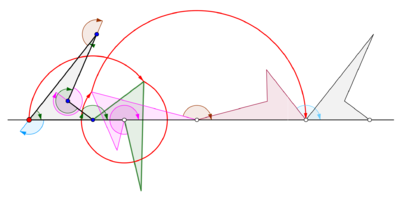
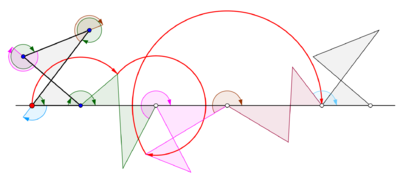
Generaliserade cykloner

En cyklogon erhålls när en polygon rullar över en rät linje. Låt det antas att den reguljära polygonen rullar över kanten på en annan polygon. Låt det också antas att spårningspunkten inte är en punkt på polygonens gräns utan möjligen en punkt inom polygonen eller utanför polygonen men som ligger i polygonens plan. I denna mer allmänna situation, låt en kurva spåras av en punkt z på en vanlig polygonal skiva med n sidor som rullar runt en annan vanlig polygonal skiva med m sidor. Kanterna på de två reguljära polygonerna antas ha samma längd. En punkt z som är stelt fast vid n-gonen spårar ut en båge som består av n cirkelbågar innan mönstret upprepas med jämna mellanrum. Denna kurva kallas en trochogon - en epitrokogon om n-gonen rullar utanför m-gonen och en hypotrokogon om den rullar inuti m-gonen. Trochogonen är kort om z är innanför n-gonen, och prolaterad (med öglor) om z är utanför n-gonen. Om z är i en vertex spårar den en epicyklogon eller en hypocyklogon.

Se även