Hoffman kärnbildningsteori

Hoffman kärnbildningsteori är en teori utvecklad av John D. Hoffman och medarbetare på 1970- och 80 - talen som försöker beskriva kristalliseringen av en polymer i termer av kinetiken och termodynamiken för polymerytkärnbildning . Teorin introducerar en modell där en yta av helt kristallin polymer skapas och introducerar ytenergiparametrar för att beskriva processen. Hoffman kärnbildningsteori är mer av en utgångspunkt för polymerkristallisationsteori och är mer känd för sina grundläggande roller i Hoffman–Weeks lamellförtjockning och Lauritzen–Hoffmans tillväxtteori .

Polymermorfologi

Amorfa regioner saknar energin som behövs för att ordna till vikta regioner som de som ses i det kristallina tillståndet

Polymerer innehåller olika morfologier på molekylär nivå som ger upphov till deras makroegenskaper. Störning på lång sikt i polymerkedjan är representativ för amorfa fasta ämnen , och kedjesegmenten anses vara amorfa. Polymerordningen med lång räckvidd liknar kristallint material, och kedjesegment anses vara kristallina.

De termiska egenskaperna hos polymerer skiljer sig fundamentalt från de för de flesta fasta material. Fasta material har vanligtvis en smältpunkt , T _m , över vilken materialet förlorar inre molekylär ordning och blir en vätska . Polymerer har både en smälttemperatur Tm _och en glasövergångstemperatur Tg _. Ovanför Tm förlorar polymerkedjorna sin molekylära ordning och uppvisar reptation _, eller rörlighet. Under Tm , men fortfarande över Tg, _förlorar polymerkedjorna en del av sin långväga rörlighet och kan bilda antingen kristallina eller amorfa regioner _. I detta temperaturområde, när temperaturen sjunker, kan amorfa områden övergå till kristallina områden, vilket gör att bulkmaterialet blir mer kristallint totalt sett. Under Tg stoppas molekylär rörelse och polymerkedjorna är väsentligen frusna på plats _. I detta temperaturområde kan amorfa områden inte längre övergå till kristallina områden, och polymeren som helhet har nått sin maximala kristallinitet.

Hoffman kärnbildningsteori tar upp den amorfa till kristallina polymerövergången, och denna övergång kan endast ske i temperaturområdet mellan _Tm och _Tg . Övergången från en amorf till en kristallin enkel polymerkedja är relaterad till den slumpmässiga termiska energin som krävs för att rikta in och vika sektioner av kedjan för att bilda ordnade regioner med titeln lameller , som är en undergrupp av ännu större strukturer som kallas sfäruliter. Kristalliseringen av polymerer kan åstadkommas med flera olika metoder och är ett komplext ämne i sig.

Kärnbildning

Kärnbildning är bildandet och tillväxten av en ny fas med eller utan närvaro av yttre yta. Närvaron av denna yta resulterar i heterogen kärnbildning medan i dess frånvaro homogen kärnbildning inträffar. Heterogen kärnbildning uppstår i fall där det finns redan existerande kärnor, såsom små dammpartiklar suspenderade i en vätska eller gas eller reagerar med en glasyta som _innehåller SiO2 . För processen för Hoffman kärnbildning och dess utveckling till Lauritzen–Hoffmans tillväxtteori är homogen kärnbildning huvudfokus. Homogen kärnbildning inträffar där inga sådana föroreningar är närvarande och ses mindre vanligt. Homogen kärnbildning börjar med små kluster av molekyler som bildas från en fas till nästa. När klustren växer, aggregeras de genom kondensation av andra molekyler. Storleken fortsätter att öka och bildar i slutändan makroskopiska droppar (eller bubblor beroende på systemet).

Kärnbildning beskrivs ofta matematiskt genom förändringen i Gibbs fria energi av n mol ånga vid ångtryck P som kondenserar till en droppe. Även kärnbildningsbarriären, vid polymerkristallisation, består av både entalpiska och entropiska komponenter som måste övervinnas. Denna barriär består av urvalsprocesser som äger rum i olika längd och tidsskalor som relaterar till de multipla regimerna senare. Denna barriär är den fria energi som krävs för att övervinna för att bilda kärnor. Det är bildningen av kärnorna från bulken till en yta som är den fria gränsytans energi. Den fria gränssnittsenergin är alltid en positiv term och verkar för att destabilisera kärnan och tillåter fortsättningen av den växande polymerkedjan. Kärnbildningen fortsätter som en gynnsam reaktion.

Termodynamik för polymerkristallisation

₀ Lauritzen–Hoffman-plotten (höger) modellerar de tre olika regimerna när (logG) + U*/k(TT ) plottas mot (TΔT) ⁻¹ . Den kan användas för att beskriva den hastighet med vilken sekundär kärnbildning konkurrerar med lateral addition vid tillväxtfronten mellan de olika temperaturerna. Denna teori kan användas för att förstå preferenserna för kärnbildning och tillväxt baserat på polymerens egenskaper inklusive dess standardsmälttemperatur.

Lauritzen–HoffmanpPlot som beskriver de tre regimerna för sekundär kärnbildning

Lamellförtjockning (Hoffman–Weeks plot)

För många polymerer är förändringen mellan den initiala lamelltjockleken vid T _c ungefär densamma som vid T _m och kan därför modelleras av Gibbs–Thomson-ekvationen ganska bra. Men eftersom det antyder att den lamellära tjockleken över det givna underkylningsintervallet (Tm _–Tc ) är oförändrad, _och många homogena kärnbildningar av polymerer innebär en förändring av tjockleken vid tillväxtfronten, eftersträvade Hoffman och Weeks en mer exakt representation. I detta avseende skapades Hoffman-Weeks plot och kan modelleras genom ekvationen

$T_{\text{m}}={T_{\text{c}} \over \beta }+(1-{1 \over \beta })T_{\text{m}}^{\circ }$

₀ där β är representativt för en förtjockningsfaktor som ges av L = L β och Tc _och Tm _är kristallisations- respektive smälttemperaturer.

Att tillämpa detta experimentellt för en konstant β möjliggör bestämning av jämviktssmälttemperaturen, T _m ° vid skärningspunkten mellan T _c och T _m .

Kinetik för polymerkristallisation

Kristalliseringsprocessen av polymerer följer inte alltid enkla kemiska hastighetsekvationer . Polymerer kan kristallisera genom en mängd olika regimer och till skillnad från enkla molekyler har polymerkristalllamellerna två mycket olika ytor. De två mest framträdande teorierna inom polymerkristallisationskinetik är Avrami-ekvationen och Lauritzen-Hoffmans tillväxtteori.

Lauritzen–Hoffmans tillväxtteori

Lauritzen-Hoffman tillväxtteorin bryter kinetiken för polymerkristallisation i slutligen två hastigheter. Modellen bryts ner i tillsats av monomerer på en växande yta. Detta initiala steg är i allmänhet associerat med kärnbildningen av polymeren. Därifrån blir kinetiken den hastighet som polymeren växer på ytan, eller den laterala tillväxthastigheten, i jämförelse med tillväxthastigheten på polymeren som förlänger kedjan, den sekundära kärnbildningshastigheten. Dessa två priser kan resultera i tre situationer.

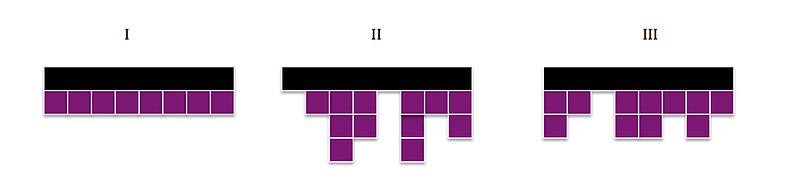
Tre regimer av kristallisationskinetik

För Regim I är tillväxthastigheten på fronten i sidled, refererad till som g , det hastighetsbestämmande steget (RDS) och överskrider den sekundära kärnbildningshastigheten , dvs. I detta fall av g >> i bildas monolager ett i taget så att om substratet har en längd av L _p och tjocklek, b , kan den totala linjära tillväxten beskrivas genom ekvationen

$G_{\text{I}}=biL_{\text{p}}$

Diagram över en kristallin polymerlameller

och hastigheten för kärnbildning i specifik kan ytterligare beskrivas av

$G_{\text{I,n}}=e^{-(K_{\text{g}}/T\Delta T)}\ ,$

med K _g lika med

$K_{\text{g}}={4b\sigma _{\text{l}}\sigma _{\text{f}}T_{ m}^{0} \over k\Delta h}$

var

σ _l är den fria energin för lateral/lamellytan per ytenhet

σ _f är vikytans fria energi per ytenhet

⁰ T _m är jämviktssmälttemperaturen

k är lika med Boltzmanns konstant

Δh är lika med förändringen av fusionsentalpi (eller latent fusionsvärme) per upprepad enhet vid standardtemperaturen

Detta visar att i region I dominerar lateral kärnbildning längs fronten framgångsrikt vid temperaturer nära smälttemperaturen, men vid mer extrema temperaturer kan andra krafter såsom diffusion påverka kärnbildningshastigheterna.

I Regim II är den laterala tillväxthastigheten antingen jämförbar eller mindre än kärnbildningshastigheten g ≤ i , vilket gör att sekundära (eller fler) skikt bildas innan det initiala skiktet har täckts. Detta gör att den linjära tillväxthastigheten kan modelleras efter

$G_{\text{II}}=b{\sqrt {ig}}$

Med antagandet att g och i är oberoende av tid, kan hastigheten med vilken nya skikt bildas approximeras och hastigheten för kärnbildning i regim II kan uttryckas som

$G_{\text{II,n}}=e^{-(K_{\text{g}}^{\prime }/T \Delta T)}\,$

med K _g^' lika med cirka 1/2 av K _g från Regim I,

$K_{\text{g}}^{\prime }={2b\sigma _{\text{l}}\sigma _{\text {f}}T_{m}^{0} \over k\Delta h}$

Slutligen skildrar Regim III i LH-modellen scenariot där lateral tillväxt inte har någon betydelse för den totala hastigheten, eftersom kärnbildningen av flera platser orsakar i >> g . Detta innebär att tillväxthastigheten kan modelleras med samma ekvation som Regim I,

$G_{\text{III}}=biL_{\text{p} }=G_{\text{III}}^{\circ }e^{{-U^{*}/k(T-T_{\text{0}})}-(K_{\text{g}} /T\Delta T)}$

där G _III^° är prefaktorn för Regim III och kan bestämmas experimentellt genom att tillämpa Lauritzen–Hoffman Plot.

Polyetenkristallisationskinetik

En rezas kristallisering beror på den tid det tar för lager av dess kedjor att vikas och orientera sig i samma riktning. Denna tid ökar med en molekyls vikt och förgrening. Tabellen nedan visar att tillväxttakten är högre för Sclair 14B.1 än Sclair 2907 (20%), där 2907 är mindre grenad än 14B.1. Här är Gc kristalltillväxthastigheten, eller hur snabbt den ordnar sig beroende på lagren, och t är den tid det tar att beställa.

Polymer	Tillväxttemperatur (°C)	G _c (μm*min ⁻¹ )	t (ms)
Sclair 2907 (20 %)	119	3,5-6,8	4,4-8,6
Sclair 14B.1	119	~0,2	~150

Ytterligare tester och tillämpningar

Många ytterligare tester har sedan genomförts för att tillämpa och jämföra Hoffmans principer med verkligheten. Bland de utförda experimenten förklaras några av de mer anmärkningsvärda sekundära kärnbildningstesterna kort i tabellen nedan.

Sekundär kärnbildningstestning	Experimentella resultat observerade
Kaliumklorid (KCl)	Sekundära kärnor bildas med en hastighet som är proportionell mot graden av underkylning (över vissa nivåer av agitation) och uppnår samma mängd kärnbildning oavsett formen på moderkristallen. Detta beror på den väsentligt större effekten av sekundär kärnbildning jämfört med primär kärnbildning av den ursprungliga kristallen. Detta bevisades genom både temperatur- och formberoende kärnstimulerade tillväxtexperiment för att bekräfta att i fall av sekundär kärnbildning endast graden och temperaturen av underkylning ändrar kärnbildningshastigheten, medan moderkristallen endast fungerar som en katalytisk initiator av processen.
Isotaktisk poly (vinylcyklohexan) (PVCH)	PVCH-kristaller visades experimentellt öka sin spridning och lateral tillväxt vid höga temperaturer, vilket indikerar att även om de inte kunde nå Regim III-temperaturer, pekar extrapolationer och hypoteser från experimentet på bekräftelse av det förväntade beteendet i var och en av de tre regimerna. Experiment drog slutsatsen att ytterligare tillväxtmekanismer som kristalltwinning och tvillinggränsinteraktioner kan förändra den traditionella LH-teorin, men ytterligare forskning behövs för att modellera varje enskild påverkan.
Zinkoxid (ZnO)	Zinkoxidkristaller visade sig genomgå sekundär kärnbildning under en udda blandning av betingelser inklusive tillsats av en diamin såväl som ytetsning. Sammantaget har testning visat att morfologin hos de sekundära kristallerna kan fluktuera mycket beroende på mängden tillsatt diamin, på grund av dess förmåga att utarma substratet och hindra tillväxten i förtid.

Se även