Foster graf

Foster-graf
Foster-graf
	Foster-grafen
Döpt efter	Ronald Martin Foster
Vertices	90
Kanter	135
Radie	8
Diameter	8
Omkrets	10
Automorfismer	4320
Kromatiskt nummer	2
Kromatiskt index	3
Könummer	2
Egenskaper	; ; ; ; Cubic Bipartite Symmetrisk Hamiltonian Distance-transitive
	Tabell över grafer och parametrar

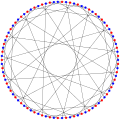
Inom det matematiska området grafteori är Foster-grafen en tvådelad 3 - regelbunden graf med 90 hörn och 135 kanter.

Foster-grafen är Hamiltonsk och har kromatiskt nummer 2, kromatiskt index 3, radie 8, diameter 8 och omkrets 10. Det är också en graf med 3 vertex och 3 -kanter . Den har kö nummer 2 och den övre gränsen på bokens tjocklek är 4.

Alla kubikavstånd -reguljära grafer är kända. Foster-grafen är en av de 13 sådana graferna. Det är den unika distanstransitiva grafen med skärningsmatrisen {3,2,2,2,2,1,1,1;1,1,1,1,2,2,2,3}. Det kan konstrueras som infallsgrafen för det partiella linjära utrymmet som är det unika trippelhöljet utan 8-goner av den generaliserade fyrkanten GQ (2,2) . Den är uppkallad efter RM Foster , vars Foster-folkräkning av kubiska symmetriska grafer inkluderade denna graf.

Den tvådelade halvan av Foster-grafen är en avstånds-reguljär graf och en lokalt linjär graf . Det är en av ett ändligt antal sådana grafer med grad sex.

Algebraiska egenskaper

Automorfismgruppen i Foster-grafen är en grupp av ordningen 4320. Den verkar transitivt på hörnen, på kanterna och på grafens bågar. Därför är Foster-grafen en symmetrisk graf . Den har automorfismer som tar vilken vertex som helst till vilken annan vertex som helst och vilken kant som helst till vilken annan kant som helst. Enligt Foster-folkräkningen är Foster-grafen, refererad till som F90A, den enda kubiska symmetriska grafen på 90 hörn.

Det karakteristiska polynomet i Foster-grafen är lika med $(x-3)(x-2)^{9}(x-1)^{18}x^{10}(x+1)^{18}(x+2)^{ 9}(x+3)(x^{2}-6)^{12}$ .

Galleri

Foster graf färgad för att markera olika cykler.
Det kromatiska numret på Foster-grafen är 2.
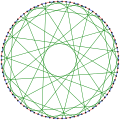
Det kromatiska indexet för Foster-grafen är 3.

Biggs, NL; Boshier, AG; Shawe-Taylor, J. (1986), "Cubic distance-regular graphs", Journal of the London Mathematical Society , 33 (3): 385–394, doi : 10.1112/jlms/s2-33.3.385 , MR 0850954 .

Van Dam, Edwin R.; Haemers, Willem H. (2002), "Spectral characterizations of some distance-regular graphs", Journal of Algebraic Combinatorics , 15 (2): 189–202, doi : 10.1023/A:1013847004932 , MR 1887234 .

Van Maldeghem, Hendrik (2002), "Ten exceptional geometries from trivalent distance regular graphs", Annals of Combinatorics , 6 (2): 209–228, doi : 10.1007/PL00012587 , MR 1955521 .