Flerdimensionell diskret faltning

Inom signalbehandling avser multidimensionell diskret faltning den matematiska operationen mellan två funktioner f och g på ett n -dimensionellt gitter som producerar en tredje funktion, också av n -dimensioner. Flerdimensionell diskret faltning är den diskreta analogen till den flerdimensionella faltningen av funktioner i det euklidiska rummet. Det är också ett specialfall av faltning på grupper när gruppen är gruppen av n -tuplar av heltal.

Definition

Problembeskrivning och grunder

I likhet med det endimensionella fallet används en asterisk för att representera faltningsoperationen. Antalet dimensioner i den givna operationen återspeglas i antalet asterisker. Till exempel skulle en M -dimensionell faltning skrivas med M asterisker. Följande representerar en M -dimensionell faltning av diskreta signaler:

$y(n_{1},n_{2},...,n_{M})=x(n_{1},n_{2},...,n_{M})*{\overset {M}{\cdots }}*h(n_{1},n_{2},...,n_{M})$

För signaler med diskret värde kan denna faltning beräknas direkt via följande:

$\ summa _{k_{1}=-\infty }^{\infty }\summa _{k_{2}=-\infty }^{\infty }...\summa _{k_{M}=-\infty }^{\infty }h(k_{1},k_{2},...,k_{M})x(n_{1}-k_{1},n_{2}-k_{2},. ..,n_{M}-k_{M})$

Det resulterande utgångsområdet för stöd för en diskret flerdimensionell faltning kommer att bestämmas baserat på storleken och stödområdena för de två insignalerna.

Visualisering av faltning mellan två enkla tvådimensionella signaler

Listade är flera egenskaper hos den tvådimensionella faltningsoperatorn. Observera att dessa även kan utökas för signaler med $N$ -dimensioner.

Kommutativ egenskap:

$x**h=h**x$

Associerad egendom:

$(x**h)**g=x**(h**g)$

Distributionsegendom:

$x**(h+g)=(x**h)+(x**g)$

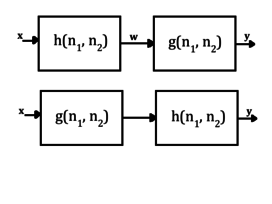
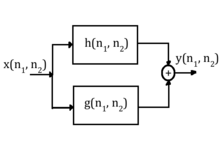
Dessa egenskaper visas i användning i figuren nedan. Givet viss ingång $x(n_{1},n_{2})$ som går in i ett filter med impulssvar $h(n_{ 1},n_{2})$ och sedan ytterligare ett filter med impulssvar $g(n_{1},n_{2})$ , utmatningen ges av $y(n_{1},n_{2})$ . Antag att utsignalen från det första filtret ges av ${\displaystyle w(n_{1},n_{2})} ,$ detta betyder att:

$w=x**h$

Vidare viks den mellanliggande funktionen sedan ihop med impulssvaret från det andra filtret, och sålunda kan utsignalen representeras av:

$y=w**g=(x**h)**g$

Med den associativa egenskapen kan detta skrivas om enligt följande:

$y=x**(h**g)$

vilket betyder att det ekvivalenta impulssvaret för ett kaskadsystem ges av:

$h_{eq}=h**g$

Båda figurerna representerar kaskadsystem. Observera att ordningen på filtren inte påverkar utgången.

En liknande analys kan göras på en uppsättning parallella system som illustreras nedan.

Ett system med en uppsättning parallella filter.

I det här fallet är det tydligt att:

$y=(x**h)+(x**g)$

Med hjälp av den distribuerande lagen, visas det att:

$y=x**(h+g)$

Detta innebär att i fallet med ett parallellt system tillhandahålls det ekvivalenta impulssvaret av:

$h_{eq}=h+g$

De ekvivalenta impulssvaren i både kaskadsystem och parallella system kan generaliseras till system med $N$ -antal filter.

Motivation och tillämpningar

Konvolution i en dimension var en kraftfull upptäckt som gjorde det möjligt att enkelt jämföra ingången och utmatningen av ett linjärt skiftinvariant (LSI) system (se LTI-systemteori ) så länge som filtersystemets impulssvar var känt. Denna uppfattning överförs också till flerdimensionell faltning, eftersom att helt enkelt känna till impulssvaret för ett flerdimensionellt filter också möjliggör en direkt jämförelse mellan ingången och utsignalen från ett system. Detta är djupgående eftersom flera av de signaler som överförs i den digitala världen idag är av flera dimensioner inklusive bilder och videor. I likhet med den endimensionella faltningen tillåter den flerdimensionella faltningen beräkning av utsignalen från ett LSI-system för en given insignal.

Tänk till exempel på en bild som skickas över ett trådlöst nätverk som utsätts för elektrooptiskt brus. Möjliga bruskällor inkluderar fel i kanalöverföring, analog till digital-omvandlaren och bildsensorn. Vanligtvis skapar brus som orsakas av kanalen eller sensorn rumsligt oberoende, högfrekventa signalkomponenter som översätts till godtyckliga ljusa och mörka fläckar på den faktiska bilden. För att befria bilddatan från det högfrekventa spektralinnehållet kan det multipliceras med frekvenssvaret för ett lågpassfilter, vilket baserat på faltningssatsen är ekvivalent med att konvolvera signalen i tids-/spatialdomänen med lågpassfiltrets impulssvar. Flera impulssvar som gör det visas nedan.

Impulssvar av typiska flerdimensionella lågpassfilter

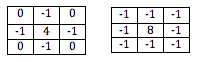
Förutom att filtrera bort spektralt innehåll kan den flerdimensionella faltningen implementera kantdetektering och utjämning. Detta är återigen helt beroende av värdena för impulssvaret som används för att konvolvera med ingångsbilden. Typiska impulssvar för kantdetektering illustreras nedan.

Typiska impulssvar för kantdetektering

Originalbild (vänster) och bild efter att ha passerat genom kantdetekteringsfilter (höger)

Förutom bildbehandling kan flerdimensionell faltning implementeras för att möjliggöra en mängd andra applikationer. Eftersom filter är utbredda i digitala kommunikationssystem, stöds alla system som måste överföra flerdimensionell data av filtreringstekniker. Det används i realtidsvideobearbetning, neurala nätverksanalyser, digital geofysisk dataanalys och mycket mer.

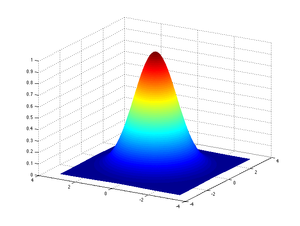
En typisk förvrängning som uppstår under bild- och videoinspelning eller överföringstillämpningar är oskärpa som orsakas av en lågpassfiltreringsprocess. Den introducerade oskärpan kan modelleras med Gaussisk lågpassfiltrering.

Originalbild (vänster) och suddig bild (höger) utförda med Gaussisk faltning

Rad-kolumnupplösning med separerbara signaler

Separerbara signaler

En signal sägs vara separerbar om den kan skrivas som produkten av flera endimensionella signaler. Matematiskt uttrycks detta som följande:

$x(n_{1},n_{2},...,n_{M})=x(n_{1})x(n_{2})...x(n_ {M})$

Några lätt igenkännbara separerbara signaler inkluderar enhetsstegfunktionen och dirac-delta-impulsfunktionen.

$u(n_{1},n_{2},...,n_{M})=u(n_{1})u(n_{2})...u(n_ {M})$ (enhetsstegfunktion)

$\delta (n_{1},n_{2},...,n_{M})=\delta (n_{1})\delta (n_{2})... \delta (n_{M})$ (dirac-delta impulsfunktion)

Konvolution är en linjär operation. Det följer sedan att den flerdimensionella faltningen av separerbara signaler kan uttryckas som produkten av många endimensionella faltningar. Tänk till exempel på fallet där x och h båda är separerbara funktioner.

$x(n_{1},n_{2})**h(n_{1},n_{2})=\summa _{k_{1}=-\infty }^{ \infty }\sum _{k_{2}=-\infty }^{\infty }h(k_{1},k_{2})x(n_{1}-k_{1},n_{2}- k_{2})$

Genom att tillämpa egenskaperna för separerbarhet kan detta sedan skrivas om som följande:

$x(n_{1},n_{2})**h(n_{1},n_{2})={\bigg (}\summa _{k_{1}=-\infty }^{\infty }h(k_{1})x(n_{1}-k_{1}){\bigg )}{\bigg (}\summa _{k_ {2}=-\infty }^{\infty }h(k_{2})x(n_{2}-k_{2}){\bigg )}$

Det är då lätt att se att detta reduceras till produkten av endimensionella veck:

$x( n_{1},n_{2})**h(n_{1},n_{2})={\bigg [}x(n_{1})*h(n_{1}){\bigg ]} {\bigg [}x(n_{2})*h(n_{2}){\bigg ]}$

Denna slutsats kan sedan utökas till faltningen av två separerbara M -dimensionella signaler enligt följande:

$x(n_{1},n_{2},...,n_{M})*{\overset {M}{\cdots }}* h(n_{1},n_{2},...,n_{M})={\bigg [}x(n_{1})*h(n_{1}){\bigg ]}{\bigg [}x(n_{2})*h(n_{2}){\bigg ]}...{\bigg [}x(n_{M})*h(n_{M}){\bigg ]}$

Så när de två signalerna är separerbara kan den flerdimensionella faltningen beräknas genom att beräkna $n_{M}$ endimensionella faltningar.

Nedbrytning av rad-kolumn

Rad-kolumnmetoden kan tillämpas när en av signalerna i faltningen är separerbar. Metoden utnyttjar egenskaperna för separerbarhet för att uppnå en metod för att beräkna faltningen av två flerdimensionella signaler som är mer beräkningseffektiv än direkt beräkning av varje sampel (förutsatt att en av signalerna är separerbar). Följande visar det matematiska resonemanget bakom rad-kolumnnedbrytningsmetoden (vanligtvis är $h(n_{1},n_{2})$ den separerbara signalen):

${\begin{aligned}y(n_{1},n_{2}) &=\summa _{k_{1}=-\infty }^{\infty }\summa _{k_{2}=-\infty }^{\infty }h(k_{1},k_{2}) x(n_{1}-k_{1},n_{2}-k_{2})\\&=\summa _{k_{1}=-\infty }^{\infty }\summa _{k_{ 2}=-\infty }^{\infty }h_{1}(k_{1})h_{2}(k_{2})x(n_{1}-k_{1},n_{2}-k_ {2})\\&=\summa _{k_{1}=-\infty }^{\infty }h_{1}(k_{1}){\Bigg [}\summa _{k_{2}= -\infty }^{\infty }h_{2}(k_{2})x(n_{1}-k_{1},n_{2}-k_{2}){\Bigg ]}\end{aligned }}$

Värdet på $\sum _{k_{2}=-\infty }^{\infty }h_{2}(k_{2})x(n_{1}-k_{1},n_{2}-k_{2})$ kan nu återanvändas vid utvärdering av andra $y$ -värden med ett delat värde på $n_{2}$ :

${\begin{aligned}y(n_{1}+\delta ,n_{2})&=\summa _{k_{1}=-\infty }^{\infty }h_{1} (k_{1}){\Bigg [}\summa _{k_{2}=-\infty }^{\infty }h_{2}(k_{2})x(n_{1}-[k_{1 }-\delta ],n_{2}-k_{2}){\Bigg ]}\\&=\summa _{k_{1}=-\infty }^{\infty }h_{1}(k_{ 1}+\delta ){\Bigg [}\sum _{k_{2}=-\infty }^{\infty }h_{2}(k_{2})x(n_{1}-k_{1} ,n_{2}-k_{2}){\Bigg ]}\end{aligned}}$

Således kan den resulterande faltningen effektivt beräknas genom att först utföra faltningsoperationen på alla raderna av ${\displaystyle x(n_{1},n_{2})} ,$ och sedan på alla av dess kolumner. Detta tillvägagångssätt kan optimeras ytterligare genom att ta hänsyn till hur minnet nås i en datorprocessor.

En processor kommer att ladda in signaldata som behövs för den givna operationen. För moderna processorer kommer data att laddas från minnet till processorns cache, som har snabbare åtkomsttider än minne. Själva cachen är uppdelad i rader. När en cache-linje laddas från minnet laddas flera dataoperander samtidigt. Tänk på det optimerade fallet där en rad med signaldata får plats helt och hållet i processorns cache. Denna speciella processor skulle kunna komma åt data radvis effektivt, men inte kolumnvis eftersom olika dataoperander i samma kolumn skulle ligga på olika cache-linjer. För att dra fördel av det sätt på vilket minnet nås, är det mer effektivt att transponera datamängden och sedan axla den radvis i stället för att försöka komma åt den kolumnvis. Algoritmen blir då:

1. Separera den separerbara tvådimensionella signalen $h(n_{1},n_{2})$$) {\displaystyle h_{1} (n_{1})}$ två endimensionella signaler och $h_{2}(n_{2})$
2. Utför radvis faltning på de horisontella komponenterna av signalen $) {\displaystyle h_{1} (n_{1})}$$\displaystyle x(n_{1},n_{2})}$ med för att erhålla $g(n_{1},n_{2})$
3. Transponera de vertikala komponenterna i signalen $g(n_{1},n_{2})$ som härrör från steg 2.
4. Utför radvis faltning på de transponerade vertikala komponenterna av $g(n_{1},n_{2})$ för att få önskad utdata ${$

Beräkningshastighet från rad-kolumnupplösning

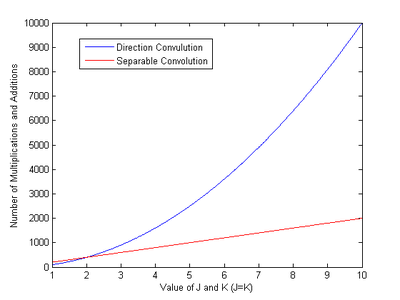
Undersök fallet där en bild av storleken $X\times Y$ passeras genom ett separerbart filter med storleken $J\times K$ . Bilden i sig är inte separerbar. Om resultatet beräknas med den direkta faltningsmetoden utan att utnyttja filtrets separerbarhet, kommer detta att kräva ungefär $XYJK$ multiplikationer och additioner. Om filtrets separerbarhet beaktas kan filtreringen utföras i två steg. Det första steget kommer att ha $XYJ$ multiplikationer och additioner och det andra steget kommer att ha ${\displaystyle XYK} ,$ vilket resulterar i totalt $XYJ+XYK$ eller $XY(J+K)$ multiplikationer och additioner. En jämförelse av beräkningskomplexiteten mellan direkt och separerbar faltning ges i följande bild:

Antal beräkningar som passerar en bild på 10 x 10 genom ett filter med storleken J x K där J = K varierar i storlek från 1 till 10

Cirkulär faltning av diskreta flerdimensionella signaler

Förutsättningen bakom den cirkulära faltningsmetoden på flerdimensionella signaler är att utveckla en relation mellan faltningssatsen och den diskreta Fouriertransformen (DFT) som kan användas för att beräkna faltningen mellan två diskreta signaler med ändlig utsträckning.

Konvolutionssats i flera dimensioner

För endimensionella signaler säger faltningssatsen att Fouriertransformen av faltningen mellan två signaler är lika med produkten av Fouriertransformerna av dessa två signaler. Således är faltning i tidsdomänen lika med multiplikation i frekvensdomänen. Matematiskt uttrycks denna princip via följande:

$$y(n)=h(n)*x(n)\longleftrightarrow Y(\ omega )=H(\omega )X(\omega )$$

Denna princip är direkt utvidgningsbar till att hantera signaler av flera dimensioner.

$$_ y(n_{1},n_{2},...,n_{M})=h(n_{1},n_{2},...,n_{M})*{\overset {M} {\cdots }}*x(n_{1},n_{2},...,n_{M})\longleftrightarrow Y(\omega _{1},\omega _{2},...,\ omega _{M})=H(\omega _{1},\omega _{2},...,\omega _{M})X(\omega _{1},\omega _{2}, ...,\omega _{M})}$$

Den här egenskapen utökas enkelt till användningen med Diskret Fourier-transform (DFT) enligt följande (observera att linjär faltning ersätts med cirkulär faltning där $\otimes$ används för att beteckna den cirkulära faltningsoperationen av storlek $N$ ):

$y(n)=h(n)\ibland x(n)\longleftrightarrow Y( k)=H(k)X(k)$

När du hanterar signaler av flera dimensioner:

$$y(n_{1},n_{2},...,n_{M})=h(n_{1},n_{2},...,n_{M})\ibland {\översatt {M} }{\cdots }}\otimes x(n_{1},n_{2},...,n_{M})\longleftrightarrow Y(k_{1},k_{2},...,k_{M })=H(k_{1},k_{2},...,k_{M})X(k_{1},k_{2},...,k_{M})$$

De cirkulära vecken här kommer att vara av storlek $N_{1},N_{2},...,N_{M}$ .

Cirkulär faltningsmetod

Motivet bakom att använda den cirkulära faltningsmetoden är att den är baserad på DFT. Utgångspunkten bakom cirkulär faltning är att ta DFT:erna för ingångssignalerna, multiplicera dem med varandra och sedan ta den inversa DFT. Försiktighet måste iakttas så att en tillräckligt stor DFT används så att aliasing inte uppstår. DFT är numeriskt beräkningsbar när den hanterar signaler av ändlig omfattning. En fördel med detta tillvägagångssätt är att eftersom det kräver att DFT och invers DFT tas, är det möjligt att använda effektiva algoritmer såsom Fast Fourier-transformen (FFT). Cirkulär faltning kan också beräknas i tids-/rumsdomänen och inte bara i frekvensdomänen.

Blockschema över cirkulär faltning med 2 M -dimensionella signaler

Välja DFT-storlek för att undvika aliasing

Betrakta följande fall där två ändliga signaler x och h tas. För båda signalerna finns en motsvarande DFT enligt följande:

$x(n_{1},n_{2})\longleftrightarrow X(k_{1},k_{2})$ och $h(n_{1},n_{2})\longleftrightarrow H(k_{1},k_{2})$

Stödområdet för $x(n_{1},n_{2})$ är $0\leq n_{1}\leq P_{1}-1$ och $0\leq n_{2}\leq P_{2}-1$ och stödområdet för ${ \displaystyle h(n_{1},n_{2})}$ är $0\leq n_{1}\leq Q_{1}-1$ och $0\leq n_{2}\leq Q_{2}-1$ .

Den linjära faltningen av dessa två signaler skulle ges som:

$$y_{linear} (n_{1},n_{2})=\summa _{m_{1}}\summa _{m_{2}}h(m_{1},m_{2})x(n_{1}-m_ {1},n_{2}-m_{2})$$

Givet stödområdena för $x(n_{1},n_{2})$ och $h(n_{1},n_ {2})$ , området för stöd för $y_{linear}(n_{1},n_{2})$ kommer då att ges som följande:

$$0\leq n_{1}\leq P_{1}+Q_{1}-1$$

$$0\leq n_{2}\leq P_{2}+Q_{2}-1$$

Baserat på stödområdena för de två signalerna måste en DFT av storlek $\displaystyle N_{1}\geq \max(P_{1},Q_{1})}$$\displaystyle N_{1}\ gånger N_{2}}$$användas$ där och $N_{2}\geq \max(P_{2} ,Q_{2})$ eftersom samma storlek DFT måste användas på båda signalerna. I händelse av att en DFT-storlek som är större än omfattningen av en signal behövs, är signalen nollpolerad tills den når den önskade längden. Efter att ha multiplicerat DFT och tagit den inversa DFT på resultatet, ges den resulterande cirkulära faltningen av:

$y_{cirkulär}(n_{1},n_{2})=\summa _{r_{1} }\summa _{r_{2}}{\Bigg [}\summa _{m_{1}=0}^{Q_{1}-1}\summa _{m_{2}=0}^{Q_{ 2}-1}h(m_{1},m_{2})x(n_{1}-m_{1}-r_{1}N_{1},n_{2}-m_{2}-r_{ 2}N_{2}){\Bigg ]}$ för $(n_{1},n_{2})\in R_{N_{1}N_ {2}}$

$R_{N_{1}N_{2}}\triangleq \ {(n_{1},n_{2}):0\leq n_{1}\leq N_{1}-1,0\leq n_{2}\leq N_{2}-1\}$

Resultatet blir att $y_{cirkulär}(n_{1},n_{2})$ kommer att vara en rumsligt aliasversion av den linjära faltningen resultat $y_{linjär}(n_{1},n_{2})$ . Detta kan uttryckas som följande:

$y_{cirkulär}(n_{1},n_{2})=\summa _{r_{1}}\summa _{r_{2}} y_{linjär}(n_{1}-r_{1}N_{1},n_{2}-r_{2}N_{2}){\mathrm {\,\,\,för\,\,\, } }(n_{1},n_{2})\i R_{N_{1}N_{2}}$

Sedan, för att undvika alias mellan de rumsligt aliasade replikerna, måste $N_{1}$ och $N_{2}$ väljas för att uppfylla följande villkor:

$N_{1}\geq P_{1}+Q_{1}-1$

$N_{2}\geq P_{2}+Q_{2}-1$

Om dessa villkor är uppfyllda kommer resultaten av den cirkulära faltningen att vara lika med den linjära faltningen (med huvudperioden för den cirkulära faltningen som stödområdet). Det är:

$y_{cirkulär}(n_{1},n_{2})= y_{linjär}(n_{1},n_{2})$ för $(n_{1},n_{2})\in R_{N_{ 1}N_{2}}$

Sammanfattning av proceduren med DFT

Konvolutionssatsen och cirkulär faltning kan alltså användas på följande sätt för att uppnå ett resultat som är lika med att utföra den linjära faltningen:

1. Välj $N_{1}$ och $N_{2}$ för att uppfylla $N_{1}\geq P_{1}+Q_{ 1}-1$ och $N_{2}\geq P_{2}+Q_{2}-1$
2. Nollställ signalerna $h(n_{1},n_{2})$ och $x(n_{1},n_{2 })$ så att de båda är $N_{1}\ gånger N_{2}$ i storlek
3. Beräkna DFT för både $h(n_{1},n_{2})$ och $x(n_{1},n_{ 2})$
4. Multiplicera resultaten av DFT för att erhålla $Y(k_{1},k_{2})=H (k_{1},k_{2})X(k_{1},k_{2})$
5. Resultatet av IDFT för $Y(k_{1},k_{2})$ kommer då att vara lika med resultatet av att utföra linjär faltning på de två signalerna

Överlappa och lägg till

En annan metod för att utföra flerdimensionell faltning är överlappnings- och tilläggsmetoden . Denna metod hjälper till att minska beräkningskomplexiteten som ofta förknippas med flerdimensionella faltningar på grund av de stora mängderna data som finns i moderna digitala system. För korthetens skull används det tvådimensionella fallet som ett exempel, men samma begrepp kan utökas till flera dimensioner.

Betrakta en tvådimensionell faltning med en direkt beräkning:

$y( n_{1},n_{2})=\summa _{k_{1}=-\infty }^{\infty }\summa _{k_{2}=-\infty }^{\infty }x(n_ {1}-k_{1},n_{2}-k_{2})h(k_{1},k_{2})$

Om man antar att utsignalen $y(n_{1},n_{2})$ har N icke-nollkoefficienter, och impulssvaret har M icke-nollsampel, skulle denna direkta beräkning behöva MN-multipliker och MN - 1 adderar för att beräkna. Om man istället använder en FFT måste filtrets frekvenssvar och Fouriertransformeringen av ingången lagras i minnet. Enorma mängder beräkningar och överdriven användning av minneslagringsutrymme utgör ett problem när fler dimensioner läggs till. Det är här metoden för överlappning och add-convolution kommer in.

Nedbrytning till mindre faltningsblock

Istället för att utföra faltning av informationsblocken i sin helhet, kan informationen delas upp i mindre block med dimensioner $L_{1}$ x $L_{2}$ vilket resulterar i mindre FFTs, mindre beräkningskomplexitet och mindre lagringsbehov. Detta kan uttryckas matematiskt på följande sätt:

$x(n_{1},n_{2})=\summa _ {i=1}^{P_{1}}\summa _{j=1}^{P_{2}}x_{ij}(n_{1},n_{2})$

där $x(n_{1},n_{2})$ representerar $N_{1}$ x $N_{2}$ insignalen , som är en summering av $P_{1}P_{2}$ blocksegment, med $P_{1}=N_{1}/L_{1 }$ och $P_{2}=N_{2}/L_{2}$ .

För att producera utsignalen utförs en tvådimensionell faltning:

$y(n_{1},n_{2})=x(n_{1}, n_{2})**h(n_{1},n_{2})$

Att ersätta $med {\displaystyle x(n_{1},n_{2})}$ resulterar i följande:

$y(n_{1} ,n_{2})=\summa _{i=1}^{P_{1}}\summa _{j=1}^{P_{2}}x_{ij}(n_{1},n_{2 })**h(n_{1},n_{2})$

Denna faltning tillför mer komplexitet än att göra en direkt faltning; Men eftersom den är integrerad med en FFT snabb faltning, fungerar overlap-add snabbare och är en mer minneseffektiv metod, vilket gör den praktisk för stora uppsättningar av flerdimensionell data.

Fördelning av proceduren

Låt $h(n_{1},n_{2})$ vara av storlek $M_{1}\ gånger M_{2}$ :

1. Bryt ingången $x(n_{1},n_{2})$ i icke-överlappande block med dimensioner $L_{1}\times L_{2 }$ .
2. Nollknapp $h(n_{1},n_{2})$ så att den har dimensioner ( $L_{1}+M_{1 }-1$ ) $\times$ ( $L_{2}+M_{2}-1$ ).
3. Använd DFT för att få $H(k_{1},k_{2})$ .
4. För varje ingångsblock:
   1. Nollpunkten $x_{ij}(n_{1},n_{2})$ ska ha dimensionerna ( $L_{1} +M_{1}-1$ ) $\times$ ( $L_{2}+M_{2}-1$ ).
   2. Ta diskret Fouriertransform av varje block för att ge $X_{ij}(k_{1},k_{2})$ .
   3. Multiplicera för att få $Y_{ij}(k_{1},k_{2}) =X_{ij}(k_{1},k_{2})H(k_{1},k_{2})$ .
   4. Ta invers diskret Fouriertransform av $Y_{ij}(k_{1},k_{2})$ för att få $y_{ij}(n_{1},n_{2})$ .
5. Hitta $y(n_{1},n_{2})$ genom att överlappa och lägga till den sista $(M_{1}-1)$$\times$$(M_{2}-1)$ exempel på $y_{ij}(n_{1},n_ {2})$ med den första $(M_{1}-1)$$\times$$(M_{2}-1)$ exempel på $y_{i+1,j+1}(n_{1},n_{2})$ för att få resultatet.

Bildmässigt arbetssätt

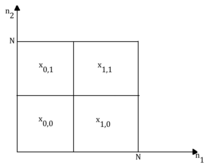
För att visualisera överlappnings-lägg-metoden tydligare undersöker följande illustrationer metoden grafiskt. Antag att ingången $x(n_{1},n_{2})$ har ett kvadratiskt områdesstöd med längden N i både vertikala och horisontella riktningar som visas i figuren nedan. Den bryts sedan upp i fyra mindre segment på ett sådant sätt att den nu är sammansatt av fyra mindre rutor. Varje block av den samlade signalen har dimensioner $(N/2)$$\times$$(N/2)$ .

Nedbruten insignal

Sedan viks varje komponent ihop med filtrets impulssvar. Observera att en fördel för en implementering som denna kan visualiseras här eftersom var och en av dessa faltningar kan parallelliseras på en dator, så länge som datorn har tillräckligt med minne och resurser för att lagra och beräkna samtidigt.

I figuren nedan representerar den första grafen till vänster faltningen som motsvarar komponenten av ingången $x_{0,0}$ med motsvarande impulssvar $h (n_{1},n_{2})$ . Till höger om det viks sedan ingången $x_{1,0}$ med impulssvaret $h(n_{1},n_{2} )$ .

Individuell komponentväxling med impulssvar

Konvoltering av varje komponent med överlappningsdelarna markerade

Samma process görs för de andra två respektive ingångarna, och de ackumuleras tillsammans för att bilda faltningen. Detta är avbildat till vänster.

Antag att filterimpulssvaret $h(n_{1},n_{2})$$) {\displaystyle (N/8)}$ ett stödområde på i båda dimensionerna. Detta innebär att varje faltning konvolverar signaler med dimensioner $(N/2)$$\times$$(N/8)$ i båda ${\ displaystyle n_{1}}$ och $n_{2}$ riktningar, vilket leder till överlappning (markerad i blått) eftersom längden på varje enskild faltning motsvarar:

$(N/2)$$+$$(N/8)$$-$$1$ = $(5/8)N-1$

åt båda hållen. Den ljusare blå delen korrelerar med överlappningen mellan två intilliggande veck, medan den mörkare blå delen korrelerar med överlappning mellan alla fyra veck. Alla dessa överlappande delar adderas tillsammans utöver faltningarna för att bilda den kombinerade faltningen $y(n_{1},n_{2})$ .

Överlappa och spara

Överlappnings- och sparametoden, precis som metoden överlappning och lägg till, används också för att minska den beräkningskomplexitet som är förknippad med diskreta tidsfaltningar. Denna metod, i kombination med FFT, tillåter att enorma mängder data kan filtreras genom ett digitalt system samtidigt som det nödvändiga minnesutrymmet som används för beräkningar på massiva datamatriser minimeras.

Jämförelse för att överlappa och lägga till

Metoden för överlappning och spara är mycket lik överlappning och lägger till metoder med några få anmärkningsvärda undantag. Överlappnings-add-metoden involverar en linjär faltning av diskreta tidssignaler, medan överlappnings-sparametoden involverar principen om cirkulär faltning. Dessutom använder överlappnings- och sparmetoden endast en engångsnollutfyllnad av impulssvaret, medan överlappnings-adderingsmetoden involverar en nollutfyllnad för varje faltning på varje ingångskomponent. Istället för att använda nollutfyllnad för att förhindra tidsdomänaliasing som dess motsvarighet för overlap-add, kasserar overlap-save helt enkelt alla aliaspunkter och sparar föregående data i ett block för att kopieras till faltningen för nästa block.

I en dimension är skillnaderna mellan prestanda och lagringsmått mellan de två metoderna minimala. I det flerdimensionella faltningsfallet föredras emellertid överlappningssparametoden framför överlappnings-add-metoden vad gäller hastighet och lagringsförmåga. Precis som i överlappnings- och tilläggsfallet åberopar proceduren det tvådimensionella fallet men kan enkelt utökas till alla flerdimensionella procedurer.

Fördelning av proceduren

Låt $h(n_{1},n_{2})$ vara av storlek $M_{1}\ gånger M_{2}$ :

1. Infoga $(M_{1}-1)$ kolumner och $(M_{2}-1)$ rader med nollor i början av insignalen $x(n_{1},n_{2})$ i båda dimensionerna.
2. Dela upp motsvarande signal i överlappande segment av dimensioner ( $L_{1}+M_{1}-1$ ) $\times$ ( ${\ displaystyle L_{2}+M_{2}-1}$ ) där varje tvådimensionellt block kommer att överlappa med $(M_{1}-1)$$\times$$(M_{2}-1)$ .
3. Nollknapp $h(n_{1},n_{2})$ så att den har dimensioner ( $L_{1}+M_{1 }-1$ ) $\times$ ( $L_{2}+M_{2}-1$ ).
4. Använd DFT för att få $H(k_{1},k_{2})$ .
5. För varje ingångsblock:
   1. Ta diskret Fouriertransform av varje block för att ge $X_{ij}(k_{1},k_{2})$ .
   2. Multiplicera för att få $Y_{ij}(k_{1},k_{2}) =X_{ij}(k_{1},k_{2})H(k_{1},k_{2})$ .
   3. Ta invers diskret Fouriertransform av $Y_{ij}(k_{1},k_{2})$ för att få $y_{ij}(n_{1},n_{2})$ .
   4. Bli av med den första $(M_{1}-1)$$\times$$(M_{2}-1)$ för varje utgångsblock $y_{ij}(n_{1},n_{2})$ .
6. Hitta $y(n_{1},n_{2})$ genom att bifoga den sista $(L_{1}\times L_{2} )$ sampel för varje utgångsblock $y_{ij}(n_{1},n_{2})$ .

Helixtransformationen

I likhet med rad-kolumnupplösning, beräknar helixtransformen den flerdimensionella faltningen genom att inkorporera endimensionella faltningsegenskaper och operatorer. Istället för att använda separerbarheten av signaler, mappar den emellertid det kartesiska koordinatutrymmet till ett spiralformigt koordinatutrymme, vilket möjliggör en avbildning från ett flerdimensionellt utrymme till ett endimensionellt utrymme.

Flerdimensionell faltning med endimensionell faltningsmetoder

För att förstå helixtransformationen är det användbart att först förstå hur en multidimensionell faltning kan brytas ner till en endimensionell faltning. Antag att de två signalerna som ska konvolveras är $X_{M\times N}$ och $Y_{K\times L}$ , vilket resulterar i en utgång $Z_{(M-K+1)\ gånger (N-L+1)}$ . Detta uttrycks på följande sätt:

$Z(i,j)=\summa _{m =0}^{M-1}\summa _{n=0}^{N-1}X(m,n)Y(im,jn)$

Därefter skapas två matriser som nollställer varje ingång i båda dimensionerna så att varje ingång har ekvivalenta dimensioner, dvs.

${\displaystyle \mathbf {X'} ={\begin{bmatrix}X&0\\0&0\\\end{bmatrix}}} och Y ′ = [ Y ]$ { $' } ={\begin{bmatrix}Y&0\\0&0\\\end{bmatrix}}}$

där var och en av inmatningsmatriserna nu har dimensioner $(M+K-1)$$\times$$(N+L- 1)$ . Det är sedan möjligt att implementera kolumnvis lexikografisk ordning för att konvertera de modifierade matriserna till vektorer, $X''$ och $Y''$ . För att minimera antalet oviktiga sampel i varje vektor, trunkeras varje vektor efter det sista samplet i de ursprungliga matriserna $X$ respektive $Y$ . Med tanke på detta ges längden på vektor $X''$ och ${\displaystyle Y''} av:$

$l_{X''}=$$(M+K-1)$$\times$$(N -1)$ + $M$

$l_{Y''}=$$(M+K-1)$$\times$$(L) -1)$ + $K$

Längden på faltningen av dessa två vektorer, $Z''$ , kan härledas och visas vara:

$l_{Z''}=$$l_{Y''}+$$l_{X''}$$=(M+K-1)$$\times$$(N+L-1)$

Denna vektorlängd är ekvivalent med dimensionerna för den ursprungliga matrisutgången ${\displaystyle Z} ,$ vilket gör konvertering tillbaka till en matris till en direkt transformation. Således omvandlas vektorn $Z''$ tillbaka till matrisform, vilket producerar utsignalen från den tvådimensionella diskreta faltningen.

Filtrering på en helix

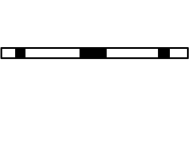
När man arbetar på ett tvådimensionellt kartesiskt nät, kommer en Fourier-transformation längs endera axlarna att resultera i att det tvådimensionella planet blir en cylinder när slutet av varje kolumn eller rad fäster vid dess respektive topp och bildar en cylinder. Filtrering på en spiral uppför sig på ett liknande sätt, förutom i detta fall fäster botten av varje kolumn till toppen av nästa kolumn, vilket resulterar i ett spiralformat nät. Detta illustreras nedan. De mörka brickorna representerar filterkoefficienterna.

Transformation från ett 2D kartesiskt filtreringsplan till ett helixfilter.

Om denna spiralformade struktur sedan skivas och lindas av till en endimensionell remsa, kommer samma filterkoefficienter på det 2-d kartesiska planet att matcha med samma indata, vilket resulterar i ett ekvivalent filtreringsschema. Detta säkerställer att en tvådimensionell faltning kommer att kunna utföras av en endimensionell faltningsoperator eftersom 2D-filtret har lindats av till ett 1D-filter med luckor på nollor som separerar filterkoefficienterna.

Endimensionell filterremsa efter att ha rullats av.

Förutsatt att ett tvådimensionellt lågpassfilter användes, såsom:

0	-1	0
-1	4	-1
0	-1	0

Sedan, när det tvådimensionella utrymmet omvandlats till en helix, skulle det endimensionella filtret se ut som följer:

$h(n)=-1,0,...,0,-1,4,-1,0,...,0,-1,0,...$

Lägg märke till i det endimensionella filtret att det inte finns några inledande nollor som visas i den endimensionella filtreringsremsan efter att ha rullats upp. Hela den endimensionella remsan kunde ha rullats ihop med; dock är det mindre beräkningsmässigt dyrt att helt enkelt ignorera de inledande nollorna. Dessutom kommer inget av dessa nollvärden på baksidan att behöva lagras i minnet, vilket bevarar värdefulla minnesresurser.

Ansökningar

Helixtransformationer för att implementera rekursiva filter via faltning används inom olika områden av signalbehandling. Även om Fourier-analys av frekvensdomän är effektiv när systemen är stationära, med konstanta koefficienter och periodiskt samplade data, blir det svårare i instabila system. Helixtransformen möjliggör tredimensionella migreringsprocesser efter stack som kan bearbeta data för tredimensionella variationer i hastighet. Dessutom kan den användas för att hjälpa till med problemet med implicit tredimensionell vågfältsextrapolering. Andra tillämpningar inkluderar användbara algoritmer för seismisk dataregularisering, prediktionsfelfilter och brusdämpning i geofysiska digitala system.

Gaussisk konvolution

En tillämpning av multidimensionell faltning som används inom signal- och bildbehandling är Gaussisk faltning. Detta syftar på att konvolvera en insignal med den Gaussiska fördelningsfunktionen.

2D Gaussisk visualisering där $\mu _{1}=\mu _{2}=0$ och $\sigma _{1}=\sigma _ {2}=1$

Gaussfördelningen samplade vid diskreta värden i en dimension ges av följande (förutsatt att ${\displaystyle \mu =0} )$ :

$$G(n)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{ -{\frac {n^{2}}{2\sigma ^{2}}}}$$

Detta utökas lätt till en signal med M dimensioner (förutsatt att $\sigma }$$\mu _{1}=\mu _{2}=...=\mu _{M}=0$ förblir konstant för alla dimensioner och ):

$${\ displaystil G(n_{1},n_{2},...,n_{M})={\frac {1}{(2\pi )^{M/2}\sigma ^{M}}}e ^{-{\frac {({n_{1}}^{2}+{n_{2}}^{2}+...+{n_{M}}^{2})}{2\sigma ^{2}}}}}$$

En viktig egenskap att känna igen är att den M -dimensionella signalen är separerbar så att:

$$G(n_{1},n_{2},...,n_{M})=G(n_{1})G(n_{2})...G(n_ {M})$$

Sedan kan Gaussisk faltning med signaler med diskreta värden uttryckas som följande:

$y(n)=x(n)*G(n)$

$y(n_{1},n_{2},...,n_{M})=x(n_{1},n_{ 2},...,n_{M})*...*G(n_{1},n_{2},...,n_{M})$

Approximation med FIR-filter

Gaussisk faltning kan effektivt approximeras via implementering av ett FIR-filter ( Finite Impulse Response) . Filtret kommer att utformas med trunkerade versioner av Gaussian. För ett tvådimensionellt filter skulle överföringsfunktionen för ett sådant filter definieras som följande:

$H(z_{1},z_{2})={\frac {1}{s(r_{1},r_{2})}}\summa _{n_{1}= -r_{1}}^{r_{1}}\summa _{n_{2}=-r_{2}}^{r_{2}}G(n_{1},n_{2}){z_{ 1}}^{-n_{1}}{z_{2}}^{-n_{2}}$

var

$s(r_{1},r_{2}) =\summa _{n_{1}=-r_{1}}^{r_{1}}\summa _{n_{2}=-r_{2}}^{r_{2}}G(n_{1 },n_{2})$

Att välja lägre värden för $r_{1}$ och $r_{2}$ kommer att resultera i att utföra färre beräkningar, men kommer att ge en mindre exakt approximation medan att välja högre värden kommer att ge en mer exakt approximation, men kommer att kräva ett större antal beräkningar.

Approximation med boxfilter

En annan metod för att approximera Gaussisk faltning är via rekursiva passeringar genom ett boxfilter. För att approximera endimensionell faltning definieras detta filter som följande:

$H(z)={\frac {1}{2r+1}}{\frac {z^{ r}-z^{-r-1}}{1-z^{-}1}}$

Vanligtvis utförs rekursiva pass 3, 4 eller 5 gånger för att erhålla en exakt approximation. En föreslagen metod för att beräkna r ges sedan som följande:

$\sigma ^{2}={\frac {1}{12}}K((2r+1)^{2}-1 )$ där K är antalet rekursiva passager genom filtret.

Sedan, eftersom den Gaussiska fördelningen är separerbar över olika dimensioner, följer det att rekursiva passeringar genom endimensionella filter (som isolerar varje dimension separat) kommer således att ge en approximation av den flerdimensionella Gaussiska faltningen. Det vill säga, M- dimensionell Gaussisk faltning skulle kunna approximeras via rekursiva passeringar genom följande endimensionella filter:

$H(z_{1})={\frac {1}{2r_{ 1}+1}}{\frac {{z_{1}}^{r_{1}}-{z_{1}}^{-r_{1}-1}}{1-{z_{1}} ^{-}1}}$

$H(z_{2})={\frac {1}{2r_{ 2}+1}}{\frac {{z_{2}}^{r_{2}}-{z_{2}}^{-r_{2}-1}}{1-{z_{2}} ^{-}1}}$

$\vdots$

$H(z_{M})={\frac {1}{2r_{ M}+1}}{\frac {{z_{M}}^{r_{M}}-{z_{M}}^{-r_{M}-1}}{1-{z_{M}} ^{-}1}}$

Ansökningar

Gaussiska faltningar används flitigt vid signal- och bildbehandling. Till exempel kan bildsuddighet åstadkommas med Gaussisk faltning där $\sigma$ styr styrkan på oskärpan. Högre värden skulle alltså motsvara ett mer suddigt slutresultat. Det används också ofta i datorseendeapplikationer som SIFT-funktionsdetektering ( Scale-invariant feature transform) .

Se även

• Veck
• Kärna (bildbehandling)
• Signalbehandling