Fläkttriangulering
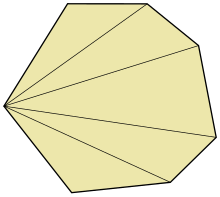
Fläkttriangulering av en konvex polygon

Fläkttriangulering av en konkav polygon med en unik konkav vertex.
I beräkningsgeometri är en solfjädertriangulering ett enkelt sätt att triangulera en polygon genom att välja en vertex och rita kanter till alla andra hörn i polygonen. Inte varje polygon kan trianguleras på detta sätt, så denna metod används vanligtvis bara för konvexa polygoner .
Egenskaper
Bortsett från egenskaperna för alla trianguleringar har fläkttrianguleringarna följande egenskaper:
- Alla konvexa polygoner, men inte alla polygoner, kan fläkttrianguleras.
- Polygoner med endast en konkav vertex kan alltid fläkttrianguleras, så länge diagonalerna är ritade från den konkava vertexen.
- Det kan vara känt om en polygon kan fläkttrianguleras genom att lösa konstgalleriproblemet , för att avgöra om det finns minst en vertex som är synlig från varje punkt i polygonen.
- Trianguleringen av en polygon med hörn använder diagonaler och genererar trianglar.
- Att generera listan med trianglar är trivialt om en ordnad lista med hörn är tillgänglig, och kan beräknas i linjär tid. Som sådan är det onödigt att explicit lagra listan med trianglar, och därför implementerar många grafiska bibliotek primitiver för att representera polygoner baserat på denna triangulering.
- Även om denna triangulering är lämplig för att lösa vissa problem, såsom rasterisering eller kollisionsdetektering , kan den vara olämplig för andra uppgifter eftersom ursprungspunkten ackumulerar ett stort antal grannar och trianguleringens inre vinklar är ojämnt fördelade.
Se även
Kategorier:


