Entropiskt värde i riskzonen

Inom finansiell matematik och stokastisk optimering används begreppet riskmått för att kvantifiera risken som är involverad i ett slumpmässigt utfall eller riskposition. Många riskåtgärder har hittills föreslagits, var och en med vissa egenskaper. Det entropiska riskvärdet ( EVAR ) är ett sammanhängande riskmått som introducerats av Ahmadi-Javid, vilket är en övre gräns för riskvärdet (VaR) och det villkorade riskvärdet (CVaR), erhållet från Chernoff-ojämlikheten . EVAR kan också representeras genom att använda begreppet relativ entropi . På grund av dess koppling till VaR och den relativa entropin kallas detta riskmått för "entropic value at risk". EVAR utvecklades för att hantera vissa beräkningsineffektivitet ^{[ förtydligande behövs ]} av CVaR. Med inspiration från den dubbla representationen av EVAR utvecklade Ahmadi-Javid en bred klass av sammanhängande riskmått , kallade g-entropiska riskmått . Både CVaR och EVAR är medlemmar i denna klass.

Definition

Låt $(\Omega ,{\mathcal {F}},P)$ vara ett sannolikhetsutrymme med $\Omega$ en uppsättning av alla enkla händelser, ${ \mathcal {F}}$ a $\sigma$ -algebra av delmängder av $\Omega$ och $P$ ett sannolikhetsmått på ${\mathcal {F}}$ . Låt $X$ vara en slumpvariabel och $\mathbf {L} _{M^{+}}$ vara mängden av alla Borels mätbara funktioner $X: \Omega \to \mathbb {R}$ vars momentgenererande funktion $M_{X}(z)$ finns för alla $z\geq 0$ . Det entropiska riskvärdet (EVaR) för $X\in \mathbf {L} _{M^{+}}$ med konfidensnivå $1-\alpha$ definieras som följer:

{\text{EVaR}}_{1-\alpha }(X):=\inf _{z>0}\left\{z^{-1}\ln \left({\frac {M_ {X}(z)}{\alpha }}\right)\right\}.

()

Inom finans används den slumpmässiga variabeln $X\in \mathbf {L} _{M^{+}},$ i ekvationen ovan för att modellera förlusterna i en portfölj.

Tänk på Chernoff-ojämlikheten

\Pr(X\geq a)\leq e^{-za}M_{X}(z),\ quad \forall z>0.

()

Att lösa ekvationen $e^{-za}M_{X}(z)=\alpha$ för $a,$ resulterar i

a_{X}(\alpha ,z):=z^{-1}\ln \left({\frac {M_{X}(z)}{\alpha }}\right).

Genom att betrakta ekvationen ( 1 ), ser vi det

{\text{EVaR}}_{1-\alpha }(X):=\inf _{z> 0}\{a_{X}(\alpha ,z)\},

som visar sambandet mellan EVAR och Chernoff-ojämlikheten. Det är värt att notera att $a_{X}(1,z)$ är det entropiska riskmåttet eller exponentiell premie , vilket är ett begrepp som används inom finans respektive försäkring.

Låt $\mathbf {L} _{M}$ vara mängden av alla Borel mätbara funktioner $X:\Omega \to \mathbb {R}$ vars momentgenererande funktion $M_{X}(z)$ finns för alla $z$ . Den dubbla representationen (eller robust representation) av EVAR är som följer:

{\text{EVaR}}_{1-\alpha }(X)=\sup _{Q\in \Im }(E_{Q}(X)),

()

där $X\in \mathbf {L} _{M},$ och $\Im$ är en uppsättning sannolikhetsmått på $(\Omega , {\mathcal {F}})$ med $\Im =\{Q\ll P:D_{KL}( Q||P)\leq -\ln \alpha \}$ . Anteckna det

D_{KL}(Q||P):=\int {\frac {dQ}{ dP}}\left(\ln {\frac {dQ}{dP}}\right)dP

är den relativa entropin av $Q$ med avseende på $P,$ även kallad Kullback–Leibler-divergensen . Den dubbla representationen av EVAR avslöjar orsaken bakom dess namngivning.

Egenskaper

EVAR är ett sammanhängande riskmått.

Den momentgenererande funktionen $M_{X}(z)$ kan representeras av EVAR: för alla $X\in \mathbf {L} _{M^ {+}}$ och $z>0$

M_{X}(z)=\sup _{0<\alpha \leq 1}\{\alpha \exp(z{\text{EVaR}}_{1-\alpha}(X))\ }.

()

För $X,Y\in \mathbf {L} _{M}$ , ${\text{EVaR} }_{1-\alpha }(X)={\text{EVaR}}_{1-\alpha }(Y)$ för alla $\alpha \in ]0,1]$ om och endast om $F_{X}(b)=F_{Y}(b)$ för alla $b\in \mathbb {R }$ .

Det entropiska riskmåttet med parametern $\theta ,$ kan representeras med hjälp av EVAR: för alla $X\in \mathbf {L} _{M^{+}}$ och $\theta >0$

\theta ^{-1}\ln M_{X}(\theta )=a_{X}(1,\theta )=\sup _{0<\alpha \leq 1}\{{\text{ EVAR}}_{1-\alpha }(X)+\theta ^{-1}\ln \alpha \}.

()

EVAR med konfidensnivå $1-\alpha$ är den snästa möjliga övre gränsen som kan erhållas från Chernoff-ojämlikheten för VaR och CVaR med konfidensnivå $1-\alpha$ ;

{\text{VaR}}(X)\leq {\text{CVaR}}(X)\leq {\text{EVaR}}(X).

()

Följande ojämlikhet gäller för EVAR:

{\text{E}}(X)\leq {\text{EVaR}}_{1-\alpha }(X)\ leq {\text{esssup}}(X)

()

där

{\text{E}}(X)

är det förväntade värdet av

X

och

{\text{esssup}}(X)

är det väsentliga högsta av

X

, dvs

\inf _{t\in \mathbb {R} }\{t:\ Pr(X\leq t)=1\}

. Så håll

{\text{EVaR}}_{0}(X)={\text{E}}(X)

och

\lim _{\alpha \to 0}{\text{EVaR}}_{1-\alpha }(X)={\text{esssup}}(X)

.

Exempel

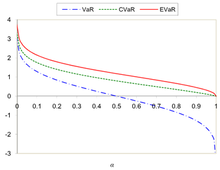
Jämför VaR, CVaR och EvaR för standardnormalfördelningen

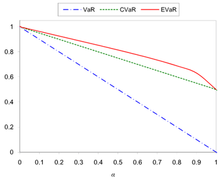
Jämföra VaR, CVaR och EvaR för den enhetliga fördelningen över intervallet (0,1)

För $X\sim N(\mu ,\sigma ^{2}),$

{\text{EVaR}}_{1-\alpha }(X)=\mu +\sigma {\sqrt {-2\ln \alpha }}.

()

För $X\sim U(a,b),$

{\text{EVaR}}_{1-\alpha }(X)=\inf _{t>0}\left\lbrace t\ln \left(t{\frac {e^{t^{ -1}b}-e^{t^{-1}a}}{ba}}\right)-t\ln \alpha \right\rbrace .

()

Figurerna 1 och 2 visar jämförelsen av VaR, CVaR och EVAR för $N(0,1)$ och $\displaystyle U(0,1)}$ .

Optimering

Låt $\rho$ vara ett riskmått. Tänk på optimeringsproblemet

\min _{{\boldsymbol {w}}\in {\boldsymbol {W}}}\rho (G({\boldsymbol {w}} ,{\boldsymbol {\psi }})),

()

där ${\displaystyle {\boldsymbol {w}}\in {\boldsymbol {W}}\subseteq \mathbb {R} ^{n}} är ett n {\displaystyle$ n $-dimensionellt$ verkligt beslut vektor, ${\boldsymbol {\psi }}$ är en $m$ -dimensionell reell slumpmässig vektor med en känd sannolikhetsfördelning och funktionen ${\displaystyle G({\boldsymbol {w}},.):\mathbb {R} ^{m}\to \mathbb {R} } är$ en Borel-mätbar funktion för alla värden ${\boldsymbol {w}}\in {\boldsymbol {W}}.$ Om $\rho ={\text{EVaR}},$ förvandlas optimeringsproblemet ( 10 ) till :

\min _{{\boldsymbol {w}}\in {\boldsymbol {W}},t>0}\left\{t\ln M_{G({\boldsymbol {w}},{\boldsymbol {\psi }})}(t^{-1})-t\ln \alpha \right\}.

()

Låt ${\boldsymbol {S}}_{\boldsymbol {\psi }}$ vara stödet för den slumpmässiga vektorn ${\boldsymbol {\psi }}.$ Om $G(.,{\boldsymbol {s}})$ är konvex för alla ${\displaystyle {\boldsymbol {s}}\i {\boldsymbol {S}}_{\boldsymbol {\psi }}} ,$ då är problemets objektiva funktion ( 11 ) också konvex. Om $G({\boldsymbol {w}},{\boldsymbol {\psi }})$ har formen

displaystyle G({\boldsymbol {w}},{\boldsymbol {\psi }})=g_{0}({\boldsymbol {w}})+\summa _{i=1}^{m}g_{i}({\boldsymbol { w}})\psi _{i},\qquad g_{i}:\mathbb {R} ^{n}\to \mathbb {R} ,i=0,1,\ldots ,m,}

()

och $\psi _{1},\ldots ,\psi _{m}$ är oberoende slumpvariabler i $\mathbf {L} _{M}$ , då ( 11 ) blir

\min _{{\boldsymbol {w}}\in {\boldsymbol {W}},t>0}\left\lbrace g_{0}({\boldsymbol {w}})+t\sum _ {i=1}^{m}\ln M_{g_{i}({\boldsymbol {w}})\psi _{i}}(t^{-1})-t\ln \alpha \right\ rbrace .

()

som är beräkningsmässigt hanteringsbar . Men för det här fallet, om man använder CVaR i problemet ( 10 ), så blir det resulterande problemet som följer:

\min _{{\boldsymbol {w}}\in {\boldsymbol {W}},t\in \mathbb {R} }\left\lbrace t+{\frac {1}{\alpha }}{ \text{E}}\left[g_{0}({\boldsymbol {w}})+\sum _{i=1}^{m}g_{i}({\boldsymbol {w}})\psi _{i}-t\right]_{+}\right\rbrace .

()

Det kan visas att genom att öka dimensionen av ${\displaystyle \psi } , är$ problemet ( 14 ) beräkningsmässigt svårlöst även för enkla fall. Antag till exempel att $\psi _{1},\ldots ,\psi _{m}$ är oberoende diskreta slumpvariabler som tar $k$ distinkta värden. För fasta värden på ${\boldsymbol {w}}$ och $t,$ är komplexiteten för att beräkna den objektiva funktionen som ges i problem ( 13 ) av ordningen $mk$ medan beräkningstiden för den objektiva funktionen av problemet ( 14 ) är av storleksordningen $k^{m}$ . Som illustration, antag att $k=2,m=100$ och summeringen av två tal tar $10^{-12}$ sekunder. För att beräkna den objektiva funktionen för problemet ( 14 ) behöver man cirka $4\x 10^{10}$ år, medan utvärderingen av problemets objektiva funktion ( 13 ) tar cirka $10^{-10}$ sekunder. Detta visar att formuleringen med EVAR överträffar formuleringen med CVaR (se för mer information).

Generalisering (g-entropiska riskmått)

Med inspiration från den dubbla representationen av EVAR som ges i ( 3 ), kan man definiera en bred klass av informationsteoretiska koherenta riskmått, som introduceras i. Låt $g$ vara en konvex riktig funktion med $g(1)=0$ och $\beta$ är ett icke-negativt tal. Det $g$ -entropiska riskmåttet med divergensnivån $\beta$ definieras som

{\text{ER}}_{g,\beta }(X):=\sup _{Q\in \Im } {\text{E}}_{Q}(X)

()

där $\Im =\{Q\ll P:H_{g}(P,Q)\leq \beta \}$ där $H_{g}(P,Q)$ är den generaliserade relativa entropin för $Q$ med avseende på $P$ . En primär representation av klassen av $g$ -entropiska riskmått kan erhållas enligt följande:

{\text{ER}}_{g, \beta }(X)=\inf _{t>0,\mu \in \mathbb {R} }\left\lbrace t\left[\mu +{\text{E}}_{P}\left( g^{*}\left({\frac {X}{t}}-\mu +\beta \right)\right)\right]\right\rbrace

()

där $g^{*}$ är konjugatet av $g$ . Genom att överväga

g(x)={\begin{cases}x\ln x&x>0\\0&x=0\\+\infty &x< 0\end{cases}}

()

med $g^{*}(x)=e^{x-1}$ och $\beta =-\ln \alpha$ , kan EVAR-formeln härledas. CVaR är också ett $g$ -entropiskt riskmått, som kan erhållas från ( 16 ) genom att ställa in

g(x)={\begin{cases}0&0\leq x\leq {\frac {1}{\alpha }}\\+\infty &{\text{annars}}\end{cases}}

()

med $g^{*}(x)={\tfrac {1}{\alpha }}\max\{0,x\}$ och $\beta =0$ (se för mer information).

För fler resultat om $g$ -entropiska riskmått se.

Disciplinerat konvext programmeringsramverk

Det disciplinerade konvexa programmeringsramverket för prov EvaR föreslogs av Cajas och har följande form:

{\begin{aligned}{\text{EVaR}}_{\alpha }(X)&=\left\{{\begin{array}{ll}{\underset {z, \,t,\,u}{\text{min}}}&t+z\ln \left({\frac {1}{\alpha T}}\right)\\{\text{st}}&z\ geq \sum _{j=1}^{T}u_{j}\\&(X_{j}-t,z,u_{j})\in K_{\text{exp}}\;\forall \ ;j=1,\ldots ,T\\\end{array}}\right.\end{aligned}}

()

där $z$ , $t$ och $u$ är variabler; $K_{\text{exp}}$ är en exponentiell kon; och $T$ är antalet observationer. Om vi definierar $w$ som vektorn av vikter för $N$ tillgångar, $r$ matrisen av avkastning och $\mu$ medelvektorn av tillgångar, kan vi posera minimeringen av den förväntade EVAR givet en nivå av förväntad portföljavkastning ${\bar {\mu }}$ enligt följande.

{\begin{aligned}&{\underset {w,\,z,\,t,\,u}{\text{min}}}&&t+z\ln \ vänster({\frac {1}{\alpha T}}\right)\\&{\text{st}}&&\mu w^{\tau }\geq {\bar {\mu }}\\&&&\ summa _{i=1}^{N}w_{i}=1\\&&&z\geq \sum _{j=1}^{T}u_{j}\\&&&(-r_{j}w^{ \tau }-t,z,u_{j})\in K_{\text{exp}}\;\forall \;j=1,\ldots ,T\\&&&w_{i}\geq 0\;;\ ;\forall \;i=1,\ldots ,N\\\end{aligned}}

()

Genom att tillämpa den disciplinerade konvexa programmeringsramen för EVAR på osammansatt kumulativ avkastningsfördelning, föreslog Cajas optimeringsproblemet för entropic drawdown at risk ( EDaR ). Vi kan posera minimeringen av den förväntade EDaR givet en nivå av förväntad avkastning ${\bar {\mu }}$ enligt följande:

{\begin{aligned}&{\underset {w,\,z,\,t,\,u,\,d}{\text{min}}}&&t+ z\ln \left({\frac {1}{\alpha T}}\right)\\&{\text{st}}&&\mu w^{\tau }\geq {\bar {\mu }} \\&&&\sum _{i=1}^{N}w_{i}=1\\&&&z\geq \sum _{j=1}^{T}u_{j}\\&&&(d_{j} -R_{j}w^{\tau }-t,z,u_{j})\in K_{\text{exp}}\;\forall \;j=1,\ldots ,T\\&&&d_{j }\geq R_{j}w^{\tau }\;\forall \;j=1,\ldots ,T\\&&&d_{j}\geq d_{j-1}\;\forall \;j=1 ,\ldots ,T\\&&&d_{j}\geq 0\;\forall \;j=1,\ldots ,T\\&&&d_{0}=0\\&&&w_{i}\geq 0\;;\; \forall \;i=1,\ldots ,N\\\end{aligned}}

()

där $d$ är en variabel som representerar den osammansatta kumulativa avkastningen för portföljen och $R$ är matrisen av oförsatt kumulativ avkastning av tillgångar.

För andra problem som riskparitet, maximering av avkastning/riskkvot eller begränsningar för maximala risknivåer för EVAR och EDaR, kan du se för mer information.

Fördelen med att modellera EvaR och EDaR använder ett disciplinerat konvext programmeringsramverk, är att vi kan använda mjukvara som CVXPY eller MOSEK för att modellera dessa portföljoptimeringsproblem. EvaR och EDaR är implementerade i pythonpaketet Riskfolio-Lib.

Se även