Ensam löpare gissning

Olöst problem i matematik :

Stämmer antagandet om ensam löpare för varje antal löpare?

(fler olösta problem i matematik)

I talteorin , närmare bestämt studien av diofantisk approximation , är den ensamma löparens gissning en gissning om det långsiktiga beteendet hos löpare på en cirkulär bana. Det sägs att $n$ löpare på en bana med enhetslängd, med konstanta hastigheter alla åtskilda från varandra, var och en kommer att vara ensamma någon gång – åtminstone $1/n$ enheter från alla andra.

Gissningen ställdes först 1967 av den tyske matematikern Jörg M. Wills, i rent talteoretiska termer, och oberoende 1974 av TW Cusick; dess illustrativa och nu populära formulering dateras till 1998. Gissningen är känd för att vara sann för 7 löpare eller färre, men det allmänna fallet förblir olöst. Implikationerna av gissningarna inkluderar lösningar på problem med sikthinder och gränser för egenskaper, relaterade till kromatiska tal, för vissa grafer.

Formulering

Exempel på ett fall av gissningar med n =6 löpare. Löpare som är färgade svarta har ännu inte varit ensamma. De vita bågarna, med längden 2/ n , indikerar att en löpare för närvarande är ensam. Gula löpare har upplevt ensamhet.

Betrakta $n$ löpare på en cirkulär bana av enhetslängd. Vid den första tiden $t=0$ är alla löpare i samma position och börjar springa; löparnas hastigheter är konstanta, alla distinkta och kan vara negativa. En löpare sägs vara ensam vid tidpunkten $t$ om de befinner sig på ett avstånd (mätt längs cirkeln) av minst $1/n$ från alla andra löpare. Lonely runner gissningen säger att varje löpare är ensam någon gång, oavsett val av hastighet.

Denna visuella formulering av gissningen publicerades första gången 1998. I många formuleringar, inklusive originalet av Jörg M. Wills, görs vissa förenklingar. Löparen som ska vara ensam står stilla vid 0 (med noll hastighet), och därför beaktas ${\displaystyle n-1} andra löpare, med hastigheter som inte är noll.$ De rörliga löparna kan begränsas ytterligare till enbart positiva hastigheter: genom symmetri har löpare med hastigheter $x$ och $-x$ samma avstånd från 0 hela tiden, och är därför i huvudsak ekvivalenta. Att bevisa resultatet för en stationär löpare innebär det allmänna resultatet för alla löpare, eftersom de kan göras stationära genom att subtrahera deras hastighet från alla löpare, vilket ger dem noll hastighet. Gissningen säger sedan att för varje samling $v_{1},v_{2},...,v_{n-1}$ av positiva, distinkta hastigheter, det finns en viss tid $t>0$ så att

$${\frac {1}{n}}\leq \operatörsnamn {frac} ( v_{i}t)\leq 1-{\frac {1}{n}}\qquad (i=1,...,n-1),$$

där $\operatorname {frac} (x)$ anger bråkdelen av $x$ . Visuellt tolkat, om löparna springer moturs, är den mellersta termen av ojämlikheten avståndet från ursprunget till i {\ $i}:$ e löparen vid tidpunkten t { $displaystyle t}$ , uppmätt moturs. Denna konvention används för resten av denna artikel. Wills gissningar var en del av hans arbete i Diophantine approximation , studien av hur nära bråk kan approximera irrationella tal.

Implikationer

Kvadrater med sidolängd 1/3 placerade vid varje halvheltalskoordinat hindrar alla strålar från origo (förutom de som ligger på en axel). Varje mindre sidolängd kommer att lämna små luckor.

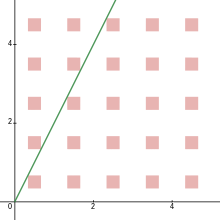
Antag att $C$ är en n - hyperkub med sidolängden $s$ i n -dimensionellt utrymme ( $n\geq 2$ ). Placera en centrerad kopia av $C$ vid varje punkt med halvheltalskoordinater . En stråle från ursprunget kan antingen missa alla kopior av $C$ , i vilket fall det finns ett (oändligt litet) gap, eller träffa minst en kopia. Cusick (1973) gjorde en självständig formulering av gissningen ensam löpare i detta sammanhang; gissningen antyder att det finns luckor om och endast om ${\displaystyle s<(n-1)/(n+1)} ,$ ignorerar strålar som ligger i en av koordinaterna hyperplan. Till exempel, placerade i ett 2-dimensionellt utrymme kommer rutor som är mindre än $1/3$$1/3}$ sidlängd att lämna luckor, som visas, och rutor med sidolängd eller större kommer att blockera varje stråle som inte är parallell med en axel. Gissningarna generaliserar denna observation till valfritt antal dimensioner.

I grafteorin har en avståndsgraf $G$ på mängden heltal, och med hjälp av någon ändlig mängd $D$ av positiva heltalsavstånd, en kant mellan $x,y$ om och endast om $|xy|\in D$ . Till exempel, om $D=\{2\}$ , är varje par i följd av jämna heltal och udda heltal intilliggande, alla tillsammans bildar två sammankopplade komponenter . A k - regelbunden färgning av heltal med steg $\lambda \in \mathbb {R}$ tilldelar varje heltal $n$ en av $k$ färger baserat på resten av $\lfloor \lambda n\rfloor$ modulo $k$ . Till exempel, om $\lambda =0.5$ , upprepas färgningen var $2k$ heltal och varje par heltal $2m,2m+1$ är samma färg. Med $k=|D|+1$ , den ensamma löparens gissning antyder att $G$ medger en korrekt k -regelbunden färgning (dvs varje nod är färgad annorlunda än dess närliggande områden) för något stegvärde. Till exempel, $(k,\lambda )=(2,0.5)$ genererar en korrekt färgning på avståndsgrafen som genereras av $D= \{2\}$ . ( $k$ är känt som det vanliga kromatiska talet för $D$ .)

Givet en riktad graf ${\displaystyle G} associerar$ ett nollflöde på $G$ ett positivt värde $f(e)$ till varje kant $e$ , t.ex. att flödet utåt från varje nod är lika med flödet inåt. Den ensamma löparens gissning innebär att om $G$ har ett nollflöde med högst $k$ distinkta heltalsvärden, så har $G$ ett nollflöde med värden endast i $\{1,2,\ldots ,k\}$ (möjligen efter att ha vänt om riktningarna för vissa bågar av $G$ ). Detta resultat bevisades för $k\geq 5$ med separata metoder, och eftersom de mindre fallen av den ensamma löparens gissning är klara, bevisas hela satsen.

Kända resultat

För en given uppsättning av löpare, låt $\delta$ beteckna det minsta av löparnas maximala avstånd för ensamhet, och gapet för ensamhet $\delta _{n}$ betecknar det minsta ${\ displaystyle \delta }$ över alla inställningar med $n$ löpare. I denna notation hävdar gissningen att ${\displaystyle \delta _{n}\geq 1/n} ,$ en gräns som, om den är korrekt, inte kan förbättras. Till exempel, om löparen som ska vara ensam är stillastående och hastigheterna $v_{i}=i$ väljs, så finns det ingen tidpunkt då de är strikt mer än $1/ n$ enheter bort från alla andra, vilket visar att $\delta _{n}\leq 1/n$ . Alternativt kan denna slutsats snabbt härledas från Dirichlets approximationssats . För ${\displaystyle n\geq 2} kan$ en enkel nedre gräns $\delta _{n}\geq 1/(2n-2)$ erhållas via ett sannolikhetsargument.

Gissningen kan reduceras till att begränsa löparnas hastigheter till positiva heltal: Om gissningen är sann för $n$ löpare med heltalshastigheter, är den sann för $n$ löpare med verkliga hastigheter.

Snävare gränser

Små förbättringar av den nedre gränsen $1/(2n-2)$ är kända. Chen & Cusick (1999) visade för $n\geq 5$ att om $2n-5$ är primtal, då $\delta _ {n}\geq {\tfrac {1}{2n-5}}$ , och om $4n-9$ är primtal, då $\delta _ {n}\geq {\tfrac {2}{4n-9}}$ . Perarnau & Serra (2016) visade ovillkorligt för tillräckligt stort $n$ att

$$\delta _{n}\geq {\frac {1}{2n-4+o(1)}}.$$

Tao (2018) bevisade det nuvarande mest kända asymptotiska resultatet: för tillräckligt stora $n$ ,

$$\delta _{n}\geq {\frac {1}{2n-2}}+{\frac {c\log n}{n^{2}(\log \log n)^{2}}}$$

för någon konstant $c>0$ . Han visade också att den fullständiga gissningen antyds genom att bevisa gissningen för heltalshastigheter av storlek $n^{O(n^{2})}$ (se big O-notation ). Denna implikation gör det teoretiskt möjligt att bevisa gissningarna för ett givet $n$ genom att kontrollera en ändlig uppsättning fall, men antalet fall växer för snabbt för att vara praktiskt.

Gissningen har bevisats under specifika antaganden om löparnas hastigheter. För tillräckligt stora $n$ gäller det if

$${\frac {v_{i+1}}{v_{i}}}\geq 1+{\frac {22\log(n-1)}{n-1}}\qquad (i=1 ,...,n-2).$$

Med andra ord gäller gissningarna för stora $n$ om hastigheterna växer tillräckligt snabbt. Om konstanten 22 ersätts med 33, så gäller antagandet för $n\geq 16343$ . Ett liknande resultat för tillräckligt stort $n$ kräver bara ett liknande antagande för $i=\lfloor n/22\rfloor -1,...,n-2$ . Ovillkorligt på $n$ är gissningen sann om $v_{i+1}/v_{i}\geq 2$ för alla $i$ .

För specifikt n

Gissningen är sann för $n\leq 7$ löpare. Bevisen för $n\leq 3$ är elementära; fallet $n=4$ etablerades 1972. $n=5$ , $n=6$ och $n=7$ mål avgjordes 1984, 2001 respektive 2008. Det första beviset för $n=5$ var datorstödd, men alla fall har sedan dess bevisats med elementära metoder.

För vissa $n$ finns det sporadiska exempel med en maximal separation på $1/n$ förutom exemplet med $v_{i}=i$ ovan. För $n=5$ är det enda kända exemplet (upp till skift och skalning) $\{0,1,3,4,7\}$ ; för $n=6$ är det enda kända exemplet $\{0,1,3,4,5,9\}$ ; och för $n=8$ är de kända exemplen $\{0,1,4,5,6,7,11 ,13\}$ och $\{0,1,2,3,4,5,7,12\}$ . Det finns en explicit oändlig familj av sådana sporadiska fall.

Kravitz (2021) formulerade en skarpare version av gissningen som tar upp nästan jämställdhetsfall. Mer specifikt antar han att för en given uppsättning hastigheter $v_{i}$ , antingen $\delta =s/(s(n) -1)+1)$ för något positivt heltal $s$ , eller $\delta \geq 1/(n-1)$ , där $\ delta$ är den konfigurationens gap av ensamhet. Han bekräftade denna gissning för $n\leq 4$ och några få specialfall.

Övriga resultat

Ett mycket starkare resultat finns för slumpmässigt valda hastigheter: med konventionen för stationär löpare, om $n$ och $\varepsilon >0$ är fasta och $n-1$ löpare med hastigheter som inte är noll väljs enhetligt slumpmässigt från $\{1,2,\ldots ,k\}$ , sedan $P(\delta \geq 1/2-\varepsilon )\to 1$ som $k\to \infty$ . Med andra ord, löpare med slumpmässiga $1/2$ någon gång "mycket ensamma" - nästan enheter från närmaste andra löpare. Den fullständiga gissningen är sann om "ensamhet" ersätts med "nästan ensam", vilket innebär att högst en annan löpare är inom $1/n$ från en given löpare. Förmodan har generaliserats till en analog i algebraiska funktionsfält .

Anteckningar och referenser

Anförda verk

• Barajas, Javier; Serra, Oriol (2008a). "Den ensamma löparen med sju löpare" . The Electronic Journal of Combinatorics . 15 (1): R48. doi : 10.37236/772 .
• ——; —— (september 2009). "På det kromatiska antalet cirkulerande grafer" . Diskret matematik . 309 (18): 5687–5696. doi : 10.1016/j.disc.2008.04.041 .
•   Betke, U.; Wills, JM (1972). "Untere schranken für zwei diophantische approximations-funktionen". Monatshefte für Mathematik . 76 (3): 214. doi : 10.1007/BF01322924 . S2CID 122549668 .
• Bienia, Wojciech; Goddyn, Luis; Gvozdjak, Pavol; Sebő, András; Tarsi, Michael (januari 1998). "Flöden, sikthinder och den ensamma löparen" . Journal of Combinatorial Theory, serie B . 72 (1): 1–9. doi : 10.1006/jctb.1997.1770 .
• Bohman, Tom ; Holzman, Ron; Kleitman, Dan (februari 2001). "Sex ensamma löpare" . The Electronic Journal of Combinatorics . 8 (2): R3. doi : 10.37236/1602 .
• Chen, Yong-Gao; Cusick, TW (januari 1999). "Problemet med sikthinder för n-dimensionella kuber" . Tidskrift för talteori . 74 (1): 126–133. doi : 10.1006/jnth.1998.2309 .
•   Chow, Sam; Rimanić, Luka (januari 2019). "Ensamma löpare i funktionsfält" (PDF) . Mathematika . 65 (3): 677–701. doi : 10.1112/S002557931900007X . S2CID 118621899 .
•   Cusick, TW (1973). "Problem med sikthinder". Aequationes Mathematicae . 9 (2–3): 165–170. doi : 10.1007/BF01832623 . S2CID 122050409 .
• —— (1974). "Problem med sikthinder i n-dimensionell geometri" . Journal of Combinatorial Theory, serie A . 16 (1): 1–11. doi : 10.1016/0097-3165(74)90066-1 .
• ——; Pomerance, Carl (1984). "Problem med sikthinder, III" . Tidskrift för talteori . 19 (2): 131–139. doi : 10.1016/0022-314X(84)90097-0 .
•   Czerwiński, Sebastian (2012). "Slumpmässiga löpare är väldigt ensamma". Journal of Combinatorial Theory, serie A . 119 (6): 1194–1199. arXiv : 1102.4464 . doi : 10.1016/j.jcta.2012.02.002 . S2CID 26415692 .
• —— (maj 2018). "Det ensamma löparproblemet för lacunary sekvenser" . Diskret matematik . 341 (5): 1301–1306. doi : 10.1016/j.disc.2018.02.002 .
• ——; Grytczuk, Jarosław (september 2008). "Osynliga löpare i ändliga fält". Informationsbehandlingsbrev . 108 (2): 64–67. doi : 10.1016/j.ipl.2008.03.019 .
• Dubickas, A. (2011). "Det ensamma löparproblemet för många löpare" . Glasnik Matematicki . 46 : 25–30. doi : 10.3336/gm.46.1.05 .
• Goddyn, L.; Wong, Erick B. (2006). "Tighta instanser av den ensamma löparen" (PDF) . Heltal . 6 (A38) . Hämtad 1 maj 2022 .
•   Kravitz, N. (2021). "Barely lonely runners and very lonely runners: a raffined approach to the Lonely Runner Problem". Kombinatorisk teori . 1 . arXiv : 1912.06034 . doi : 10.5070/C61055383 . S2CID 245100000 .
•   Perarnau, Guillem; Serra, Oriol (mars 2016). "Korrelation bland löpare och några resultat på den ensamma löparens gissning" . The Electronic Journal of Combinatorics . 23 (1): P1,50. doi : 10.37236/5123 . S2CID 7039062 .
• Renault, J. (2004). "Syshinder: Ett kortare prov för 6 ensamma löpare" . Diskret matematik . 287 (1–3): 93–101. doi : 10.1016/j.disc.2004.06.008 .
• Tao, Terence (31 december 2018). "Några kommentarer om den ensamma löparens gissning" . Bidrag till diskret matematik . 13 : nr 2 (2018). doi : 10.11575/cdm.v13i2.62728 .
•   Wills, Jörg M. (1967). "Zwei sätze über inhomogene diophantische approximation von irrationalzehlen". Monatshefte für Mathematik . 71 (3): 263–269. doi : 10.1007/BF01298332 . S2CID 122754182 .

externa länkar

• Artikel i Open Problem Garden nr. 4, 551-562.