Ellingham–Horton graf
| Ellingham–Horton-grafer | |
|---|---|
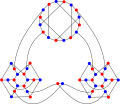
 Ellingham–Horton 54-grafen.
| |
| Döpt efter | Joseph Horton och Mark Ellingham |
| Vertices |
54 (54-graf) 78 (78-graf) |
| Kanter |
81 (54-graf) 117 (78-graf) |
| Radie |
9 (54-graf) 7 (78-graf) |
| Diameter |
10 (54-graf) 13 (78-graf) |
| Omkrets | 6 (båda) |
| Automorfismer |
32 (54-graf) 16 (78-graf) |
| Kromatiskt nummer | 2 (båda) |
| Kromatiskt index | 3 (båda) |
| Boktjocklek | 3 (båda) |
| Könummer | 2 (båda) |
| Egenskaper |
Kubisk (båda) Tvådelad (båda) Regelbunden (båda) |
| Tabell över grafer och parametrar | |
Inom det matematiska området grafteori är Ellingham –Horton-graferna två 3- regelbundna grafer på 54 och 78 hörn: Ellingham–Horton 54-grafen och Ellingham–Horton 78-grafen . De är uppkallade efter Joseph D. Horton och Mark N. Ellingham , deras upptäckare. Dessa två grafer ger motexempel till förmodan av WT Tutte att varje kubik 3-kopplad tvådelad graf är Hamiltonsk . Boktjockleken på Ellingham-Horton 54-grafen och Ellingham - Horton 78-grafen är 3 och kön nummer 2.
Det första motexemplet till Tutte-förmodan var Horton-grafen , publicerad av Bondy & Murty (1976) . Efter Horton-grafen hittades ett antal mindre motexempel till Tutte-förmodan. Bland dem finns en graf med 92 vertex av Horton (1982) , en graf med 78 vertex av Owens (1983) och de två Ellingham-Horton-graferna.
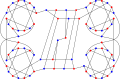
Den första Ellingham–Horton-grafen publicerades av Ellingham (1981) och är av storleksordningen 78. Vid den tiden var det det minsta kända motexemplet till Tutte-förmodan. Den andra Ellingham–Horton-grafen publicerades av Ellingham & Horton (1983) och är av ordning 54. 1989 upptäcktes Georges graf, den minsta för närvarande kända icke-Hamiltonska 3-kopplade kubiska tvådelade grafen, innehållande 50 hörn.
Galleri
Det kromatiska numret på Ellingham–Horton 54-grafen är 2.
Det kromatiska indexet för Ellingham–Horton 54-grafen är 3.
Det kromatiska numret på Ellingham–Horton 78-grafen är 2.
Det kromatiska indexet för Ellingham–Horton 78-grafen är 3.