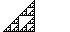Ducci-sekvens

En Ducci-sekvens är en sekvens av n -tuplar av heltal , ibland känd som "Diffy-spelet", eftersom det är baserat på sekvenser.

Givet en n -tuppel av heltal $(a_{1},a_{2},...,a_{n})$ , nästa n - tupel i sekvensen bildas genom att ta de absoluta skillnaderna mellan angränsande heltal:

(a_{1},a_{2},...,a_{n})\högerpil (|a_{1}-a_{2}|,|a_{2}-a_{3}|, ...,|a_{n}-a_{1}|)\,.

Ett annat sätt att beskriva detta är som följer. Ordna n heltal i en cirkel och skapa en ny cirkel genom att ta skillnaden mellan grannar, ignorera eventuella minustecken; upprepa sedan operationen. Ducci-sekvenser är uppkallade efter Enrico Ducci (1864 - 1940), den italienske matematikern som upptäckte detta på 1930-talet.

Ducci-sekvenser är också kända som Ducci-kartan eller n-nummerspelet . Det finns fortfarande öppna problem i studien av dessa kartor.

Egenskaper

Från den andra n -tupeln och framåt är det tydligt att varje heltal i varje n -tuppel i en Ducci-sekvens är större än eller lika med 0 och är mindre än eller lika med skillnaden mellan maximi- och minimummedlemmarna i det första n - tuppel. Eftersom det bara finns ett ändligt antal möjliga n -tupler med dessa begränsningar måste sekvensen av n-tupler förr eller senare upprepa sig. Varje Ducci-sekvens blir därför så småningom periodisk .

Om n är en potens av 2 når varje Ducci-sekvens så småningom n -tuppeln (0,0,...,0) i ett ändligt antal steg.

Om n inte är en potens av två, kommer en Ducci-sekvens antingen så småningom att nå en n -tuppel av nollor eller kommer att lägga sig i en periodisk slinga av 'binära' n -tuplar; det vill säga n -tupler av formen $k(b_{1},b_{2},...b_{n})$ , ${\ displaystyle k}$ är en konstant, och $b_{i}\in \{0,1\}$ .

En uppenbar generalisering av Ducci-sekvenser är att tillåta medlemmarna i n -tuplarna att vara valfria reella tal snarare än bara heltal. Till exempel konvergerar denna 4-tuppel till (0, 0, 0, 0) i fyra iterationer: $(e,\pi ,{\sqrt {2}},1)\högerpil (\pi -e ,\pi -{\sqrt {2}},{\sqrt {2}}-1,e-1)\högerpil (e-{\sqrt {2}},\pi -2{\sqrt {2}} +1,e-{\sqrt {2}},2e-\pi -1)\högerpil$ $(\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1,\pi -e -{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1)\högerpil (0,0,0,0)$

De egenskaper som presenteras här håller inte alltid för dessa generaliseringar. Till exempel en Ducci-sekvens som börjar med n -tupeln (1, q , q ² , q ³ ) där q är den (irrationella) positiva roten av kubiken $x^ {3}-x^{2}-x-1=0$ når inte (0,0,0,0) i ett begränsat antal steg, även om det i gränsen konvergerar till (0,0,0,0 ).

Exempel

Ducci-sekvenser kan vara godtyckligt långa innan de når en tupel av nollor eller en periodisk loop. Den 4-tuppelsekvens som börjar med (0, 653, 1854, 4063) tar 24 iterationer för att nå nolltupeln.

${\displaystyle (0,5416,0,5416,02,02,0,653,02) 9 4063) \rightarrow (548,1008,1854,3410)$ $stil \cdots \rightarrow (0,0,128,128)\rightarrow (0,128,0,128)\rightarrow (128,128,128,128)\rightarrow (0,0,0,0)}$

Denna 5-tuppelsekvens går in i en period 15 binär 'loop' efter 7 iterationer.

${\begin{matrix}15799\rightarrow &42208\rightarrow &20284\rightarrow &22642\rightarrow &04220\rightarrow &42020\rightarrow \\22224\rightarrow &00022\rightarrow &00202\rightarrow &02222\rightarrow &20002\rightarrow &20020\rightarrow \\20222\rightarrow &22000\rightarrow &02002\rightarrow &22022\rightarrow &02200\rightarrow &20200\rightarrow \\22202\rightarrow &00220\rightarrow &02020\rightarrow &22220\rightarrow &00022\rightarrow &\cdots \quad \quad \\\end{matrix}}$

Följande 6-tuppelsekvens visar att sekvenser av tupler vars längd inte är en potens av två fortfarande kan nå en tuppel med nollor:

${\begin{matrix}121210\rightarrow &111111\rightarrow &000000\\\end{matrix}}$

Om vissa villkor ställs på någon "potens av två"-tuppel Ducci-sekvens, skulle det ta kraften av två eller mindre iterationer för att nå nolltupeln. Det antas att dessa sekvenser överensstämmer med en regel.

Modulo två form

När Ducci-sekvenserna går in i binära loopar är det möjligt att behandla sekvensen i modulo två. Det är:

(|a_{1}-a_{2}|,|a_{2}-a_{3}|,...,|a_{n}-a_{1}|)\ =(a_{1}+a_{2},a_{2}+a_{3},...,a_{n}+a_{1}){\bmod {2}}

Detta utgör grunden för att bevisa när sekvensen försvinner till alla nollor.

Cellulära automater

Den linjära kartan i modulo 2 kan vidare identifieras som den cellulära automaten betecknad som regel 102 i Wolfram-kod och relaterad till regel 90 genom Martin-Odlyzko-Wolfram-kartan. Regel 102 återger Sierpinski-triangeln .

Andra relaterade ämnen

Ducci-kartan är ett exempel på en differensekvation , en kategori som även inkluderar icke-linjär dynamik , kaosteori och numerisk analys . Likheter med cyklotomiska polynom har också påpekats. Även om det inte finns några praktiska tillämpningar av Ducci-kartan för närvarande, ledde dess koppling till det mycket tillämpade fältet för differensekvationer till gissningar om att en form av Ducci-kartan också kan komma att användas i framtiden.

externa länkar