Droz-Farny linjesats

Linjen genom $A_{0},B_{0},C_{0}$ är Droz-Farny linje

Inom euklidisk geometri är Droz -Farnys linjesats en egenskap hos två vinkelräta linjer genom ortocentrum av en godtycklig triangel.

Låt $T$ vara en triangel med hörn $A$ , $B$ och $C$ , och låt $H$ vara dess ortocentrum (den gemensamma punkten för dess tre höjdlinjer . Låt $L_{1}$ och $L_{2}$ vara två ömsesidigt vinkelräta linjer genom $H$ . Låt $A_{1 }$ , $B_{1}$ och $C_{1}$ är punkterna där $L_{1}$ skär sidolinjerna $BC$ , $CA$ respektive $AB$ . På samma sätt låter vi $A_{2}$ , $B_{2}$ och ${ \displaystyle C_{2}}$ är punkterna där $L_{2}$ skär dessa sidolinjer. Droz-Farnys linjesats säger att mittpunkterna för de tre segmenten $A_{1 }A_{2}$ , $B_{1}B_{2}$ och $C_{1}C_{2}$ är kolinjära .

Teoremet uttalades av Arnold Droz-Farny 1899, men det är inte klart om han hade ett bevis.

Goormagighths generalisering

En generalisering av Droz-Farny linjesatsen bevisades 1930 av René Goormaghtigh .

Som ovan, låt $T$ vara en triangel med hörn $A$ , $B$ och $C$ . Låt $P$ vara vilken punkt som helst skild från $A$ , $B$ och $C$ , och $L$ vara vilken linje som helst genom $P$ . Låt $A_{1}$ , $B_{1}$ och $C_{1}$ vara punkter på sidolinjerna $BC$ , $CA$ , respektive $AB$ , så att linjerna $PA_{1}$ , $PB_{1}$ och ${ \displaystyle PC_{1}}$ är bilderna av linjerna $PA$ , $PB$ , respektive $PC$ , genom reflektion mot linjen $L$ . Goormaghtighs sats säger då att punkterna $A_{1}$ , $B_{1}$ och $C_{1}$ är kolinjära.

Droz-Farnys linjesats är ett specialfall av detta resultat, när $P$ är ortocentrum för triangeln $T$ .

Daos generalisering

Teoremet generaliserades ytterligare av Dao Thanh Oai. Generaliseringen som följer:

Första generaliseringen: Låt ABC vara en triangel, P vara en punkt på planet, låt tre parallella segment AA', BB', CC' så att dess mittpunkter och P är kolinjära. Sedan möter PA', PB', PC' BC, CA, AB respektive vid tre kolinjära punkter.

Daos andra generalisering

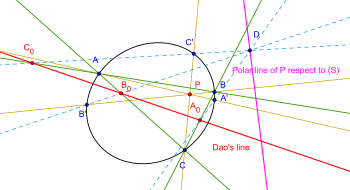
₀₀₀₀₀₀ Andra generaliseringen: Låt en konisk S och en punkt P på planet . Konstruera tre linjer d _a , d _b , d _c genom P så att de möter könen vid A, A'; B, B'; C, C' respektive. Låt D vara en punkt på polen av punkt P med avseende på (S) eller D ligger på könen (S). Låt DA' ∩ BC =A ; DB' ∩ AC = B ; DC' ∩ AB= C . Då är A , B , C kolinjära.