Delaunay tessellation field estimator
Delaunay tessellation field estimator (DTFE) , (eller Delone tessellation field estimator (DTFE)) är ett matematiskt verktyg för att rekonstruera ett volymtäckande och kontinuerligt densitet eller intensitetsfält från en diskret punktuppsättning. DTFE har olika astrofysiska tillämpningar, såsom analys av numeriska simuleringar av kosmisk strukturbildning , kartläggning av universums storskaliga struktur och förbättring av datorsimuleringsprogram för kosmisk strukturbildning. Den har utvecklats av Willem Schaap och Rien van de Weijgaert. Den största fördelen med DTFE är att den automatiskt anpassar sig till (starka) variationer i densitet och geometri. Den är därför mycket väl lämpad för studier av storskalig galaxfördelning.
Metod
DTFE består av tre huvudsteg:
.jpg)
Steg 1
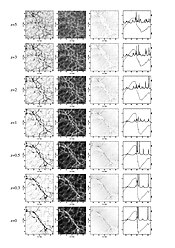
Utgångspunkten är en given diskret poängfördelning. I figurens övre vänstra ram är en punktfördelning inritad där i mitten av ramen finns ett föremål vars densitet minskar radiellt utåt. I det första steget av DTFE Delaunay-tesselationen av punktfördelningen. Detta är en volymtäckande indelning av rymden i trianglar (tetraedrar i tre dimensioner), vars hörn bildas av punktfördelningen (se figur, övre högra ramen). Delaunay-tesselationen definieras så att inuti det inre av den omslutna cirkeln av varje Delaunay-triangel finns inga andra punkter från den definierande punktfördelningen.
Steg 2
Delaunays tessellation utgör hjärtat av DTFE. I figuren syns det tydligt att tessellationen automatiskt anpassar sig till både den lokala tätheten och geometrin för punktfördelningen: där tätheten är hög är trianglarna små och vice versa. Storleken på trianglarna är därför ett mått på punktfördelningens lokala täthet. Denna egenskap hos Delaunay-tesselationen utnyttjas i steg 2 av DTFE, där den lokala densiteten uppskattas vid platserna för provtagningspunkterna. För detta ändamål definieras densiteten vid platsen för varje provtagningspunkt som inversen av arean av dess omgivande Delaunay-trianglar (gånger en normaliseringskonstant, se figur, nedre högra ram).
Steg 3
I steg 3 interpoleras dessa densitetsuppskattningar till vilken annan punkt som helst, genom att anta att inuti varje Delaunay-triangel varierar täthetsfältet linjärt (se figur, nedre vänstra ramen).
Ansökningar
En atlas över det närliggande universum
En av huvudapplikationerna för DTFE är återgivningen av vårt kosmiska grannskap. Nedan visas DTFE-rekonstruktionen av 2dF Galaxy Redshift Survey , som avslöjar en imponerande bild av de kosmiska strukturerna i det närliggande universum. Flera superkluster sticker ut, som Sloan Great Wall , en av de största strukturerna i universum.
2dF Galaxy Redshift Survey
DTFE-rekonstruktion av de inre delarna av 2dF Galaxy Redshift Survey
Numeriska simuleringar av strukturbildning
De flesta algoritmer för att simulera kosmisk strukturbildning är partikelhydrodynamiska koder. Kärnan i dessa koder är den utjämnade partikelhydrodynamiska (SPH) densitetsuppskattningsproceduren. Att ersätta den med DTFE-densitetsuppskattningen kommer att ge en stor förbättring för simuleringar som innehåller återkopplingsprocesser, som spelar en stor roll i galax- och stjärnbildning .
Kosmiskt hastighetsfält
DTFE har designats för att rekonstruera densitets- eller intensitetsfält från en diskret uppsättning oregelbundet fördelade punkter som samplar detta fält. Det kan emellertid också användas för att rekonstruera andra kontinuerliga fält som har samplas vid dessa punkters lägen, till exempel det kosmiska hastighetsfältet. Användningen av DTFE för detta ändamål har samma fördelar som den har för att rekonstruera täthetsfält. Fälten rekonstrueras lokalt utan tillämpning av en artificiell eller användarberoende utjämningsprocedur , vilket resulterar i en optimal upplösning och dämpning av skottbruseffekter . De uppskattade kvantiteterna är volymtäckande och möjliggör en direkt jämförelse med teoretiska förutsägelser.
Evolution och dynamik i det kosmiska nätet
DTFE har utformats speciellt för att beskriva de komplexa egenskaperna hos den kosmiska webben. Den kan därför användas för att studera utvecklingen av tomrum och superkluster i storskalig materiagalaxfördelning.
Utveckling av ett tomrum
Utvecklingen av en superkluster
externa länkar
- DTFE: The Delaunay Tessellation Field Estimator , Willem Schaap, 2007, doktorsavhandling, Rijksuniversiteit Groningen, Nederländerna
- NASA Astronomi Dagens bild: The Sloan Great Wall: Största kända strukturen? (7 november 2007)
- Undersöka kosmiska hastighetsflöden i lokaluniversum , Emilio Romano-Diaz, 2004, doktorsavhandling, Rijksuniversiteit Groningen, Nederländerna
- Den kosmiska webben: geometrisk analys , Rien van de Weygaert och Willem Schaap, 2004
