De 85 sätten att knyta en slips

De 85 sätten att knyta en slips

Författare	Thomas Fink och Yong Mao
Utgivare	Fjärde ståndet
Publiceringsdatum	4 november 1999
ISBN	1-84115-249-8
OCLC	59397523

De 85 sätten att knyta en slips är en bok av Thomas Fink och Yong Mao om historien om den knutna halsduken , den moderna slipsen och hur man knyter var och en. Den är baserad på två matematiska artiklar publicerade av författarna i Nature och Physica A medan de var forskare vid Cambridge Universitys Cavendish Laboratory . Författarna bevisar att, om man antar att både slipsen och bäraren är av typisk storlek, finns det exakt 85 sätt att knyta en slips med den konventionella metoden att vira den breda änden av slipsen runt den smala änden. De beskriver var och en och lyfter fram de som de anser vara historiskt anmärkningsvärda eller estetiskt tilltalande.

Den publicerades av Fourth Estate den 4 november 1999 och publicerades därefter på nio andra språk.

Matematiken

Upptäckten av alla möjliga sätt att knyta en slips beror på en matematisk formulering av handlingen att knyta en slips. I sina uppsatser (som är tekniska) och bok (som är till för en lekmannapublik, förutom en bilaga), visar författarna att slipsknutar är likvärdiga med ihållande slumpmässiga promenader på ett triangulärt galler, med vissa begränsningar för hur promenaderna börjar och slutet. Att räkna upp slipknutar med n drag är alltså likvärdigt med att räkna upp vandringar på n steg. Genom att påtvinga villkoren för symmetri och balans reduceras de 85 knutarna till 13 estetiska.

Knut representation

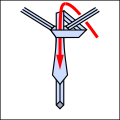
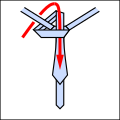
Grundtanken är att slipsknoppar kan beskrivas som en sekvens av fem olika möjliga drag, även om inte alla drag kan följa varandra. Dessa sammanfattas enligt följande. Alla diagram är som slipsen skulle se ut om du hade den på dig och tittade i spegeln.

• L : vänster; C : centrum; R : höger; dessa måste ändra varje rörelse.
• i : in i diagrammet; o : ut ur diagrammet; dessa måste växla.
• T : genom den nyss gjorda öglan.

Med denna stenografi kan traditionella och nya knutar uttryckas kompakt, enligt nedan. Observera att varje knut som börjar med ett o- drag måste börja med att slipsen vänds ut och in runt halsen.

• Exempel på knytband.
• 

  Li börjar.

• 

  Låg början.

• 

  Lo

• 

  Ro

• 

  Li

• 

  Ri

• 

  Lo Ri Co T slut.

• 

  Ro Li Co T slut.

Knutar

Urvalskriterier

Av de 85 möjliga knutarna med en typisk slips valde Fink och Mao ut tretton som "estetiska knutar" lämpliga för användning. De gjorde sitt urval baserat på tre kriterier: form, symmetri och balans.

Form

I Fink och Maos klassificering tillhör var och en av de 85 slipsknopparna en viss "klass", som definieras av dess totala antal drag och dess antal centreringsdrag. Till exempel är fyra-i-handen en knut med fyra drag, en-center, medan halv-Windsor är en sex-rörelse, två-center knut. Knutar med färre centrerande rörelser, mindre än en tredjedel av det totala antalet, verkar smalare och mer långsträckta, medan knutar med fler centreringsrörelser verkar bredare och mer knäböjda. På grund av den triangulära karaktären hos slipknutar måste antalet centreringsdrag nödvändigtvis vara mindre än hälften av det totala antalet drag.

Det finns totalt 16 klasser, allt från tre drag med ett center till nio drag med fyra center, men endast klasser där förhållandet mellan centreringsdrag och totala drag är 1:6 eller mer innehåller en estetisk knut, vilket eliminerar tre klasser ( tio knop) för återstående 13 klasser, med 75 knop. (I Nature -tidningen placerades den nedre gränsen till en mer restriktiv 1:4, vilket eliminerade knutklasserna som innehöll Kelvin, Victoria och Grantchester; detta reviderades troligen specifikt för att inkludera Victoria/Prince Albert, som har ganska omfattande historisk dokumentation.) Den mest representativa knuten i varje återstående klass valdes sedan ut utifrån symmetri och balans.

Symmetri

Symmetri i fallet med knutar kan hänvisa till två möjliga egenskaper: visuell symmetri (i vilken utsträckning knuten tycks vara identiskt utformad på vänster och höger sida) och matematisk symmetri (antalet L- och R-rörelser är lika nära lika som möjligt). Fink och Mao hänvisar till det senare, även om vissa knutar som är något asymmetriska (som Nicky och Windsor) verkar symmetriska för ögat. Endast knutar med lika många L- och R-drag kan vara matematiskt symmetriska, medan resten av de estetiska knutarna nödvändigtvis kommer att ha ett större L- eller R-drag.

Balans

Fink och Mao beskriver balans som "i vilken utsträckning rörelserna är väl blandade", och citerar en hårdare knut som lossnar mindre lätt som sin främsta dygd. Den beräknas med en viss formel, men kan bäst förstås av lekmannen som i vilken grad L-, R- och C-rörelserna är jämnt fördelade över knutningssekvensen, och i vilken utsträckning LR- eller RL-mönstret fortsätter oavbrutet efter icke-terminala centreringsrörelser (vilket kräver en ändring av lindningsriktningen från moturs till medurs, eller vice versa). Var och en av de estetiska knutarna visar dessa egenskaper.

Ett antal knutar har praktiskt taget identiska varianter, som skiljer sig åt genom transponeringen av L- och R-par. Till exempel är en variant av Half-Windsor, Li Ro Ci Lo Ri Co T (Knut 7), knuten Li Ro Ci Ro Li Co T (Knut 8), ibland kallad Co-Half-Windsor. Hänvisningar till Half-Windsor i litteraturen hänvisar ibland till den ena, ibland till den andra. För bokens syfte, när en knut har minst en variant (dvs. när två eller flera knutar, med den största graden av symmetri för sin klass, delar samma grundläggande struktur förutom ett eller flera transponerade LR-par), mest balanserade versionen får standardbeteckningen, medan de andra är märkta som varianter, oavsett egenskaper som att vara självutlösande (lösgörs när den smala änden dras ut). Således får den mer balanserade av de två "halv-Windsor"-knutarna en lägre numrering och namnet "Half-Windsor", även om den något mindre balanserade "co-Half-Windsor"-varianten är lika känd som "Half-Windsor" Windsor" i herrstilslitteraturen, och har fördelen av att vara självutlösande, och det vanligaste sättet att knyta Windsor-knuten kallas "co-Windsor 3" av Fink och Mao. Detta är dock inte avsett att markera en estetisk preferens för en variant framför den andra; som författarna noterar i sina tidskriftsartiklar, "Vi försöker inte skilja mellan dessa knutar och deras motsvarigheter; så mycket överlåter vi till läsarens eget gottfinnande."

Tre av de estetiska knutarna (St Andrew, Cavendish och Grantchester) har samma symmetri och balansvärden som minst en annan knut i sin klass; i det här fallet verkar de ha valts ut baserat på hur jämnt de fördelar de obalanserade delarna genom knuten. Detta kan lätt ses när man ser dessa knutar som kombinationer av två mindre knutar, eftersom balansvärdena för varje komponent summeras till balansvärdet för den slutliga knuten. I obalanserade knutar där balansvärdet är udda, bryts det upp så att den mer obalanserade delen av de två placeras mot början av knuten. Detta är förmodligen avsett att hjälpa den yttersta delen av knuten att behålla sin form och förbli tät.

De 13 estetiska knutarna

De tretton estetiska knutarna som beskrivs i boken, i storleksordning, är följande. Terminalsekvenser (de sista tre dragen som slutar med knutningen) är i fetstil. Knutarna betecknas ibland enbart av deras nummer (t.ex. FM2 för fyran, där FM står för Fink-Mao). En knut är självlösgörande om, när den tunna änden dras ut genom knuten, ingen knut finns kvar; eftersom alla knutar börjar till vänster är en knut självfrigörande om terminalsekvensen är Ro Li Co ; den är inte självfrigörande om terminalsekvensen är Lo Ri Co. Symmetri och självutlösande är i komplementär distribution för knutar med den största graden av balans för sin klass.

siffra	Sekvens	namn	Självutlösande	Symmetrisk
1.	Lo Ri Co T	Liten knut	Nej	Ja
2.	Li Ro Li Co T	Fyra i handen	Ja	Nej
3.	Lo Ri Lo Ri Co T	Kelvin	Nej	Ja
4.	Lo Ci Ro Li Co T	Nicky (självsläppande Pratt)	Ja	Nej
6.	Li Ro Li Ro Li Co T	Victoria	Ja	Nej
7.	Li Ro Ci Lo Ri Co T	Halv-Windsor	Nej	Ja
12.	Lo Ri Lo Ci Ro Li Co T	St Andrew	Ja	Nej
18.	Lo Ci Ro Ci Lo Ri Co T	Plattsburgh	Nej	Ja
23.	Li Ro Li Co Ri Lo Ri Co T	Cavendish	Nej	Ja
31.	Li Co Ri Lo Ci Ro Li Co T	Windsor	Ja	Nej
44.	Lo Ri Lo Ri Co Li Ro Li Co T	Grantchester	Ja	Nej
54.	Lo Ri Co Li Ro Ci Lo Ri Co T	Hannover	Nej	Ja
78.	Lo Ci Ro Ci Lo Ci Ro Li Co T	Balthus	Ja	Nej

Tre vanliga variantknutar är följande. De ingår för deras gemensamma egenskaper (Pratt, Half-Windsor-variant), eller för att vara självutlösande när deras mer "estetiska" motsvarigheter inte är det (Half-Windsor-variant, Hannover-variant). Half-Windsor och Hannover-varianterna har fördelen av att vara både symmetriska och självutlösande, men är mindre balanserade än deras motsvarigheter ovan:

siffra	Sekvens	namn	Självutlösande	Symmetrisk
5.	Lo Ci Lo Ri Co T	Pratt	Nej	Nej
8.	Li Ro Ci Ro Li Co T	Halv-Windsor variant	Ja	Ja
55.	Lo Ri Co Ri Lo Ci Ro Li Co T	Hannover variant	Ja	Ja

Recensioner

Boken recenserades i Nature , The Daily Telegraph , The Guardian , GQ , Physics World och andra.

externa länkar

• Slipsar knutar på Curlie
• Jeff Banks handledning om hur man knyter en slips