Dominerande set

Tre dominerande uppsättningar av samma graf (i rött). Dominanstalet för denna graf är 2: (b) och (c) visar att det finns en dominerande mängd med 2 hörn, och det finns ingen dominerande mängd med bara 1 hörn.

I grafteorin är en dominerande uppsättning för en graf $G$ en delmängd $D$ av dess hörn, så att varje hörn av $G$ är antingen i $D$ eller har en granne i $D$ . Dominanstalet $γ() är$ G antalet hörn i en minsta dominerande mängd för $G$ .

Det dominerande uppsättningsproblemet gäller att testa om $γ(G) \leq K$ för en given graf $G$ och ingång $K$ ; det är ett klassiskt NP-komplett beslutsproblem inom beräkningskomplexitetsteori . Därför tror man att det kanske inte finns någon effektiv algoritm som kan beräkna $γ(G)$ för alla grafer $G$ . Det finns dock effektiva approximationsalgoritmer , såväl som effektiva exakta algoritmer för vissa grafklasser.

Dominerande uppsättningar är av praktiskt intresse inom flera områden. Inom trådlöst nätverk används dominerande uppsättningar för att hitta effektiva rutter inom ad-hoc-mobilnätverk. De har också använts i dokumentsammanfattningar och vid design av säkra system för elnät .

Formell definition

Givet en oriktad graf $G = (V, E)$ kallas en delmängd av hörn ${\displaystyle D\subseteq V} en$ dominerande mängd om för varje vertex $u\in V\setminus D$ , det finns en vertex $v\in D$ så att $(u,v)\in E$ .

Varje graf har minst en dominerande mängd: om $D=V=$ mängden av alla hörn, så är D per definition en dominerande mängd, eftersom det inte finns någon vertex $u\in V\setminus D$ . En mer intressant utmaning är att hitta små dominerande set. Dominanstalet för $G$ definieras som: $\gamma (G):=\min\{|D|:D{\text{ är en dominerande uppsättning av }}G\}$ | .

Varianter

En ansluten dominerande mängd är en dominerande mängd som också är ansluten . Om S är en sammankopplad dominerande mängd kan man bilda ett spännande träd av G där S bildar uppsättningen av icke-bladiga hörn av trädet; omvänt, om T är något spännande träd i en graf med mer än två hörn, bildar de icke-bladiga hörnen av T en ansluten dominerande mängd. Att hitta minsta anslutna dominerande uppsättningar motsvarar därför att hitta spännande träd med maximalt antal löv.

En total dominerande mängd (eller starkt dominerande mängd ) är en uppsättning hörn så att alla hörn i grafen, inklusive hörnen i själva den dominerande mängden, har en granne i den dominerande mängden. Det vill säga: för varje vertex $u\in V$ , finns det en vertex $v\in D$ så att $(u,v) \i E$ . Figur (c) ovan visar en dominerande uppsättning som är en sammankopplad dominerande uppsättning och en total dominerande uppsättning; exemplen i figurerna (a) och (b) är ingetdera. I motsats till en enkel dominerande uppsättning kanske en total dominerande uppsättning inte existerar. Till exempel, en graf med en eller flera hörn och inga kanter har inte en total dominerande uppsättning. Det starka dominanstalet för $G$ definieras som: $\gamma ^{strong}(G):=\min\{|D|:D{\text{ är en starkt dominerande uppsättning av }}G\}$ ; uppenbarligen, $\gamma ^{strong}(G)\geq \gamma (G)$ .

En dominerande kantuppsättning är en uppsättning kanter (vertexpar) vars förening är en dominerande uppsättning; en sådan uppsättning kanske inte finns (till exempel, en graf med en eller flera hörn och inga kanter har det inte). Om den existerar, är föreningen av alla dess kanter en starkt dominerande uppsättning. Därför är den minsta storleken på en kantdominerande uppsättning åtminstone $\gamma ^{strong}(G)/2$ .

Däremot är en kantdominerande uppsättning en uppsättning D av kanter, så att varje kant som inte är i D ligger intill åtminstone en kant i D ; en sådan uppsättning finns alltid (till exempel är uppsättningen av alla kanter en kantdominerande uppsättning).

En k -dominerande uppsättning är en uppsättning av hörn så att varje vertex som inte ingår i uppsättningen har minst k grannar i uppsättningen (en standarddominerande uppsättning är en 1-dominerande uppsättning). På liknande sätt är en k -tuppeldominerande uppsättning en uppsättning av hörn så att varje vertex i grafen har minst k grannar i uppsättningen (en total dominerande uppsättning är en en-tuppeldominerande uppsättning). En $(1 + log n)$ -approximation av en minsta dominerande mängd av k -tupel kan hittas i polynomtid. Varje graf tillåter en k -dominerande mängd (till exempel mängden av alla hörn); men endast grafer med minsta grad $k - 1$ tillåter en k -tuppeldominerande mängd. Men även om grafen tillåter k -tuppeldominerande uppsättning, kan en minsta k -tuppeldominerande uppsättning vara nästan k gånger så stor som en minsta k -dominerande uppsättning för samma graf; En $(1,7 + log Δ)$ -approximation av en minsta k -dominerande mängd kan också hittas i polynomtid.

En stjärndominerande mängd är en delmängd D av V så att, för varje vertex v i V , skär stjärnan av v (uppsättningen av kanter som gränsar till v ) stjärnan av någon vertex i D . Tydligen, om G har isolerade hörn så har den inga stjärndominerande uppsättningar (eftersom stjärnan i isolerade hörn är tom). Om G inte har några isolerade hörn, är varje dominerande mängd en stjärndominerande mängd och vice versa. Skillnaden mellan stjärnherravälde och vanlig dominans är mer påtaglig när deras bråkvarianter beaktas.

En domatisk partition är en uppdelning av hörnen i disjunkta dominerande uppsättningar. Det domatiska numret är den maximala storleken på en domatisk partition.

En evigt dominerande mängd är en dynamisk version av dominans där en vertex v i dominerande mängd D väljs och ersätts med en granne u ( u är inte i D ) så att den modifierade D också är en dominerande mängd och denna process kan upprepas över någon oändlig sekvens av val av hörn v .

Dominerande och oberoende uppsättningar

Dominerande mängder är nära besläktade med oberoende mängder : en oberoende mängd är också en dominerande mängd om och bara om den är en maximal oberoende mängd , så varje maximal oberoende mängd i en graf är nödvändigtvis också en minimal dominerande mängd.

Dominans av oberoende uppsättningar

En dominerande uppsättning kan vara en oberoende uppsättning eller inte. Till exempel visar figurerna (a) och (b) ovan oberoende dominerande uppsättningar, medan figur (c) illustrerar en dominerande uppsättning som inte är en oberoende uppsättning.

Det oberoende dominanstalet $i (G)$ i en graf $G$ är storleken på den minsta dominerande mängden som är en oberoende mängd. På motsvarande sätt är det storleken på den minsta maximala oberoende uppsättningen. Minimum i $i (G)$ tas över färre element (endast de oberoende uppsättningarna beaktas), så $γ (G) \leq i (G)$ för alla grafer $G$ .

Olikheten kan vara strikt - det finns grafer $G$ för vilka $γ (G) < i (G)$ . Låt till exempel $G$ vara dubbelstjärnegrafen som består av hörn $x_{1},\ldots ,x_{p},a, b,y_{1},\ldots ,y_{q}$ , där $p, q > 1$ . Kanterna på $G$ definieras enligt följande: varje $x i$ är intill $a$ , $a$ är intill $b$ och $b$ är intill varje $y j$ . Då $γ(G) = 2$ eftersom ${a, b}$ är en minsta dominerande mängd. Om $p \leq q$ , då $i (G) = p + 1$ eftersom $\{x_{1},\ldots ,x_{p},b\}$ är en minsta dominerande mängd som också är oberoende (det är en minsta maximalt oberoende mängd).

Det finns graffamiljer där $γ(G) = i (G)$ , det vill säga varje minsta maximala oberoende mängd är en minsta dominerande mängd. Till exempel, $γ(G) = i (G)$ om $G$ är en klofri graf .

En graf $G$ kallas en dominans-perfekt graf om $γ (H) = i (H)$ i varje inducerad subgraf $H$ av $G$ . Eftersom en inducerad subgraf av en klofri graf är klofri, följer det att alla klofria grafer också är dominans-perfekta.

För varje graf $G är$ dess linjegraf $L (G)$ klofri, och följaktligen är en minsta maximal oberoende mängd i $L (G)$ också en minsta dominerande mängd i $L (G)$ . En oberoende mängd i $L (G)$ motsvarar en matchning i $G$ , och en dominerande mängd i L $(G) motsvarar$ en kantdominerande mängd i $G.$ Därför har en minsta maximal matchning samma storlek som en minsta kantdominerande uppsättning.

Dominans av oberoende uppsättningar

Oberoendedominanstalet $iγ (G)$ för en graf $G$ är det maximala, över alla oberoende mängder $A$ av $G$ , av den minsta mängden som dominerar $A$ . Dominerande delmängder av hörn kräver potentiellt färre hörn än att dominera alla hörn, så $iγ (G) \leq γ (G)$ för alla grafer $G$ .

Olikheten kan vara strikt - det finns grafer $G$ för vilka $iγ (G) < γ (G)$ . Till exempel, för något heltal $n$ , låt $G$ vara en graf där hörnen är raderna och kolumnerna på ett $n$ -by- $n-$ kort, och två sådana hörn är sammankopplade om och bara om de skär varandra. De enda oberoende uppsättningarna är uppsättningar av endast rader eller uppsättningar av endast kolumner, och var och en av dem kan domineras av en enda vertex (en kolumn eller en rad), så $iγ (G) = 1$ . Men för att dominera alla hörn behöver vi minst en rad och en kolumn, så $γ (G) = 2$ . Dessutom kan förhållandet mellan $y (G)/ iy (G)$ vara godtyckligt stort. Till exempel, om hörn av $G$ är alla delmängder av kvadrater på en $n$ -by- $n$ tavla, då är fortfarande $iγ (G) = 1$ , men $γ (G) = n$ .

Det bi-oberoende dominanstalet $iγi (G)$ för en graf $G$ är det maximala, över alla oberoende uppsättningar $A$ av $G$ , av den minsta oberoende uppsättningen som dominerar $A$ . Följande relationer gäller för alla grafer $G$ :

{\begin{aligned}i(G)&\geq \gamma (G)\geq i\gamma (G)\\i(G)&\geq i\gamma i(G)\geq i\gamma (G)\end{aligned}}

Historia

Dominansproblematiken studerades från 1950-talet och framåt, men forskningstakten om dominans ökade markant i mitten av 1970-talet. 1972 visade Richard Karp att uppsättningsomslagsproblemet var NP-komplett . Detta hade omedelbara implikationer för det dominerande uppsättningsproblemet, eftersom det finns enkla spetsar att sätta och kant till icke-disjunkande skärnings-bijektioner mellan de två problemen. Detta visade att det dominerande setproblemet också var NP-komplett .

Algoritmer och beräkningskomplexitet

Set cover problemet är ett välkänt NP-hårt problem – beslutsversionen av set covering var ett av Karps 21 NP-kompletta problem . Det finns ett par polynom-tid L-reduktioner mellan det minsta dominerande uppsättningsproblemet och uppsättningstäckningsproblemet . Dessa minskningar ( se nedan ) visar att en effektiv algoritm för det minsta dominerande uppsättningsproblemet skulle ge en effektiv algoritm för uppsättningstäckningsproblemet, och vice versa. Dessutom bevarar reduktionerna approximationsförhållandet : för varje α, skulle en polynom-tid α-approximationsalgoritm för minsta dominerande mängder tillhandahålla en polynom-tid α-approximationsalgoritm för mängdtäckningsproblemet och vice versa. Båda problemen är i själva verket Log-APX-kompletta .

Approximabiliteten för settäckning är också väl förstått: en logaritmisk approximationsfaktor kan hittas genom att använda en enkel girig algoritm, och att hitta en sublogaritmisk approximationsfaktor är NP-svårt. Mer specifikt ger den giriga algoritmen en faktor $1 + log| V |$ approximation av en minsta dominerande mängd, och ingen polynomtidsalgoritm kan uppnå en approximationsfaktor bättre än $c log| V |$ för vissa $c > 0$ om inte P = NP .

L-reduktioner

Följande två reduktioner visar att det minsta dominerande mängdproblemet och mängdtäckningsproblemet är ekvivalenta under L-reduktioner : givet en instans av ett problem kan vi konstruera en likvärdig instans av det andra problemet.

Från dominerande set till settäckning

Givet en graf $G = (V, E)$ med $V = {1, 2, ..., n},$ konstruera en uppsättning täckningsinstans $(U, S)$ enligt följande: universum $U$ är $V$ , och familjen av delmängder är $S = {S 1, S 2, ..., Sn} så$ att $Sv intill$ består av vertex $v$ och alla hörn $v$ i $G$ .

Om $D nu$ är en dominerande mängd för $G$ , så är $C = {S v : v \in D}$ en genomförbar lösning på mängdtäckningsproblemet, med $| C | = | D |$ . Omvänt, om $C = {S v : v \in D}$ är en genomförbar lösning på mängdtäckningsproblemet, då är $D$ en dominerande mängd för $G$ , med $| D | = | C |$ .

Därför är storleken på en minsta dominerande uppsättning för $U, S) G$ $lika$ med storleken på en minimiuppsättning för ( . Dessutom finns det en enkel algoritm som mappar en dominerande uppsättning till en uppsättningsomslag av samma storlek och vice versa. I synnerhet tillhandahåller en effektiv a-approximationsalgoritm för uppsättningstäckning en effektiv a-approximationsalgoritm för minsta dominerande uppsättningar.

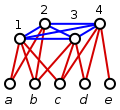
Till exempel, givet grafen

G

som visas till höger, konstruerar vi en uppsättning täckningsinstans med universum

U = {1, 2, ..., 6}

och delmängderna

S 1 = {1, 2, 5},

S 2 = {1, 2, 3, 5},

S 3 = {2, 3, 4, 6},

S 4 = {3, 4},

S 5 = {1, 2, 5, 6}

och

S 6 = {3, 5, 6}.

I det här exemplet är

D = {3, 5}

en dominerande mängd för

G

– detta motsvarar mängden omslag

C = {S 3, S 5}. Till exempel

domineras vertex

4 \in V av vertex

3 \in D

, och elementet

4 \in U

ingår i mängden

S 3 \in C

.

Från settäckande till dominerande set

Låt $(S, U) vara en instans$ $av S = {Si : i \in I };$ mängdtäckningsproblemet med universum $U$ och familjen av delmängder vi antar att $U$ och indexuppsättningen $I$ är disjunkta. Konstruera en graf $G = (V, E)$ enligt följande: uppsättningen av hörn är $V = I \cup U$ , det finns en kant ${i, j} \in E$ mellan varje par $i, j \in I$ , och det finns också en kant ${i, u}$ för varje $i \in I$ och $u \in Si .$ Det vill säga, $G$ är en delad graf : $I$ är en klick och $U$ är en oberoende mängd .

Om nu $C = {Si : i \in D}$ är en genomförbar lösning av mängdtäckningsproblemet för någon delmängd $D \subseteq I$ , så är $D$ en dominerande mängd för $G$ , med $| D | = | C |$ : Först, för varje $u \in U$ finns det ett $i \in D$ så att $u \in S i$ , och genom konstruktion är $u$ och $i$ intilliggande i $G$ ; därför domineras $u av$ $i$ . För det andra, eftersom $D$ måste vara icke-tom, är varje $i \in I$ intill en vertex i $D$ .

Omvänt, låt $D$ vara en dominerande mängd för $G$ . Då är det möjligt att konstruera en annan dominerande mängd $X$ så att $| X | \leq | D |$ och $X \subseteq I$ : ersätt helt enkelt varje $u \in D \cap U$ med en granne $i \in I$ till $u$ . Då $är C = {Si : i \in X}$ en genomförbar lösning på problemet med uppsättningstäckning, med $| C | = | X | \leq | D |$ .

Illustrationen till höger visar konstruktionen för

U = {a, b, c, d, e}, I = {1, 2, 3, 4},

S 1 = {a, b, c},

S 2 = {a, b},

d, e} . S4 = {c S3

, = {b, c, d}

och

; I C = {S1, S4}

det här exemplet är ett uppsättningsomslag detta motsvarar den dominerande mängden

D = {1, 4}.

D = {a, 3, 4}

är en annan dominerande uppsättning för grafen

G

. Givet

D

kan vi konstruera en dominerande mängd

X = {1, 3, 4}

som inte är större än

D

och som är en delmängd av

I

. Den dominerande mängden

X

motsvarar mängden täcker

C = {S 1, S 3, S 4}.

Speciella fall

Om grafen har maximal grad Δ, så hittar den giriga approximationsalgoritmen en $O (log Δ)$ -approximation av en minsta dominerande mängd. Låt också $d g$ vara kardinaliteten för dominerande mängd som erhålls med girig approximation då följande relation gäller, $d_{g}\leq N+1-{\sqrt {2M+ 1}}$ , där $N$ är antalet noder och $M$ är antalet kanter i en given oriktad graf. För fast Δ kvalificeras detta som en dominerande uppsättning för APX- medlemskap; i själva verket är den APX-komplett.

Problemet tillåter ett polynom-tidsapproximationsschema (PTAS) för speciella fall som enhetsdiskdiagram och plana grafer . En minsta dominerande uppsättning kan hittas i linjär tid i serie-parallella grafer .

Exakta algoritmer

En minsta dominerande uppsättning av en $n$ -vertex-graf kan hittas i tiden $O (2 n n)$ genom att inspektera alla vertex-delmängder. Fomin, Grandoni & Kratsch (2009) visar hur man hittar en minsta dominerande mängd i tid $O (1,5137 n)$ och exponentiellt rum, och i tid $O (1,5264 n)$ och polynomrum. En snabbare algoritm, som använder $O (1,5048 n)$ tid hittades av van Rooij, Nederlof & van Dijk (2009), som också visar att antalet minsta dominerande uppsättningar kan beräknas under denna tid. Antalet minimala dominerande uppsättningar är som mest $1,7159 n$ och alla sådana uppsättningar kan listas i tiden $O (1,7159 n)$ .

Parameteriserad komplexitet

Att hitta en dominerande uppsättning av storlek $k$ spelar en central roll i teorin om parameteriserad komplexitet. Det är det mest välkända problemet som är komplett för klassen W[2] och används i många reduktioner för att visa svårigheter med andra problem. I synnerhet är problemet inte löserbart med fasta parametrar i den meningen att ingen algoritm med körtid $f (k) nO (1)$ för någon funktion $f$ existerar såvida inte W-hierarkin kollapsar till FPT=W[2].

Å andra sidan, om ingångsgrafen är plan förblir problemet NP-hårt, men en algoritm med fasta parametrar är känd. Faktum är att problemet har en kärna med storleken linjär i $k$ , och körtider som är exponentiella i √ k och kubik i $n$ kan erhållas genom att tillämpa dynamisk programmering på en grennedbrytning av kärnan. Mer allmänt är problemet med den dominerande uppsättningen och många varianter av problemet lösta med fasta parametrar när de parametriseras av både storleken på den dominerande uppsättningen och storleken på den minsta förbjudna fullständiga tvådelade subgrafen ; det vill säga problemet är FPT på biclique-fria grafer , en mycket allmän klass av glesa grafer som inkluderar de plana graferna.

Den komplementära uppsättningen till en dominerande uppsättning, en icke-blockerare , kan hittas av en algoritm med fasta parametrar på vilken graf som helst.

Se även

Vizings gissning - relaterar dominanstalet för en kartesisk produkt av grafer till dominanstalet för dess faktorer.
Ställskyddsproblem
Bondage nummer
Nonblocker - komplementet till en dominerande uppsättning.

Anteckningar

Alber, Jochen; Fellows, Michael R ; Niedermeier, Rolf (2004), "Polynomial-time data reduction for dominating set", Journal of the ACM , 51 (3): 363–384, arXiv : cs/0207066 , doi : 10.1145/990308.990309 , S825C0ID 1 .
Allan, Robert B.; Laskar, Renu (1978), "On domination and independent domination numbers of a graph", Discrete Mathematics , 23 (2): 73–76, doi : 10.1016/0012-365X(78)90105-X .
Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek ; Woeginger, Gerhard (2000), "Minimum dominerande uppsättning", A Compendium of NP Optimization Problems .
Dehne, Frank; Fellows, Michael; Fernau, Henning; Prieto, Elena; Rosamond, Frances (2006), "Nonblocker: Parameterized algorithmics for minimum dominating set" (PDF) , SOFSEM 2006: 32nd Conference on Current Trends in Theory and Practice of Computer Science, Merin, Tjeckien, 21-27 januari 2006, Proceedings , Lecture Notes in Computer Science, vol. 3831, Springer, s. 237–245, doi : 10.1007/11611257_21 .
Escoffier, Bruno; Paschos, Vangelis Th. (2006), "Fullständighet i approximationsklasser bortom APX", Theoretical Computer Science , 359 (1–3): 369–377, doi : 10.1016/j.tcs.2006.05.023
Faudree, Ralph ; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics , 164 (1–3): 87–147, doi : 10.1016/S0012-365X(96)00045-3 , MR 143222 .
Fomin, Fedor V.; Grandoni, Fabrizio; Kratsch, Dieter (2009), "A measure & conquer approach for the analysis of exact algorithms", Journal of the ACM , 56 (5): 25:1–32, doi : 10.1145/1552285.1552286 , S2CID 1186651 .
Fomin, Fedor V.; Grandoni, Fabrizio; Pyatkin, Artem; Stepanov, Alexey (2008), "Kombinatoriska gränser via mäta och erövra: Bounding minimal dominating sets and applications", ACM Transactions on Algorithms , 5 (1): 9:1–17, doi : 10.1145/1435375.1435384 , S4894ID 7 .
Fomin, Fedor V.; Thilikos, Dimitrios M. (2006), "Dominating sets in planar graphs: branch-width and exponential speed-up", SIAM Journal on Computing , 36 (2): 281, doi : 10.1137/S0097539702419649 , S232CID 8 .
Förster, Klaus-Tycho. (2013), "Approximating Fault-Tolerant Domination in General Graphs", Proc. of the Tenth Workshop on Analytic Algorithmics and Combinatorics ANALCO , SIAM, s. 25–32, doi : 10.1137/1.9781611973037.4 , ISBN 978-1-61197-254-2 .
Garey, Michael R .; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness , W.H. Freeman , ISBN 0-7167-1045-5 , sid. 190, problem GT2.
Hedetniemi, ST; Laskar, RC (1990), "Bibliography on domination in graphs and some basic definitions of domination parameters", Discrete Mathematics , 86 (1–3): 257–277, doi : 10.1016/0012-365X(90)90365-O .
Kann, Viggo (1992), On the Approximability of NP-complete Optimization Problems (PDF) . Doktorsavhandling, Institutionen för numerisk analys och datavetenskap, Kungliga Tekniska Högskolan , Stockholm {{ citation }} : CS1 underhåll: efterskrift ( länk ) .
Klasing, Ralf; Laforest, Christian (2004), "Hardness results and approximation algorithms of k-tuple domination in graphs", Information Processing Letters , 89 (2): 75–83, doi : 10.1016/j.ipl.2003.10.004 .
Papadimitriou, Christos H.; Yannakakis, Mihailis (1991), "Optimization, Approximation, and Complexity Classes", Journal of Computer and System Sciences , 43 (3): 425–440, doi : 10.1016/0022-0000(91)90023-X
Parekh, Abhay K. (1991), "Analysis of a greedy heuristic for finding small domining sets in graphs", Information Processing Letters , 39 (5): 237–240, doi : 10.1016/0020-0190(91)90021-9
Raz, R .; Safra, S. (1997), "A sub-constant error-probability low-grade test, and sub-constant error-probability PCP characterization of NP", Proc . 29th Annual ACM Symposium on Theory of Computing , ACM, s. 475–484, doi : 10.1145/258533.258641 , ISBN 0-89791-888-6 , S2CID 15457604 .
Takamizawa, K.; Nishizeki, T .; Saito, N. (1982), "Linear-time computability of combinatorial problems on series–parallel graphs", Journal of the ACM , 29 (3): 623–641, doi : 10.1145/322326.322328 , S2CID 540821 .
Telle, Jan Arne; Villanger, Yngve (2012), "FPT algorithms for domination in biclique-free graphs", i Epstein, Leah; Ferragina, Paolo (red.), Algorithms – ESA 2012: 20th Annual European Symposium, Ljubljana, Slovenien, 10–12 september 2012, Proceedings , Lecture Notes in Computer Science , vol. 7501, Springer, s. 802–812, doi : 10.1007/978-3-642-33090-2_69 .
van Rooij, JMM; Nederlof, J.; van Dijk, TC (2009), "Inclusion/Exclusion Meets Measure and Conquer: Exact Algorithms for Counting Dominating Sets", Proc. 17th Annual European Symposium on Algorithms, ESA 2009 , Lecture Notes in Computer Science, vol. 5757, Springer, s. 554–565, doi : 10.1007/978-3-642-04128-0_50 , ISBN 978-3-642-04127-3 .

Vidare läsning

Grandoni, F. (2006), "A note on the complexity of minimum dominating set", Journal of Discrete Algorithms , 4 (2): 209–214, CiteSeerX 10.1.1.108.3223 , doi : 10.1016/j.jda.2005.03. .002 .
Guha, S.; Khuller, S. (1998), "Approximationsalgoritmer för anslutna dominerande uppsättningar" (PDF) , Algorithmica , 20 (4): 374–387, doi : 10.1007/PL00009201 , hdl : 1903/8321 , S29C1ID 2 .
Haynes, Teresa W. ; Hedetniemi, Stephen; Slater, Peter (1998a), Fundamentals of Domination in Graphs , Marcel Dekker, ISBN 0-8247-0033-3 , OCLC 37903553 .
Haynes, Teresa W. ; Hedetniemi, Stephen; Slater, Peter (1998b), Domination in Graphs: Advanced Topics , Marcel Dekker, ISBN 0-8247-0034-1 , OCLC 38201061 .
West, Douglas B. (2001), Introduktion till grafteori (2 uppl.), Pearson Education .