Biryukovs ekvation

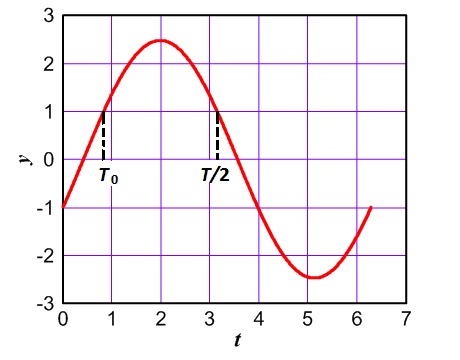
Sinusoscillationer F = 0,01

Biryukov-ekvationen ( eller Biryukov-oscillatorn ), uppkallad efter Vadim Biryukov (1946), är en icke-linjär andra ordningens differentialekvation som används för att modellera dämpade oscillatorer .

Ekvationen ges av

${\frac {d^{2}y}{dt^{2}}}+f(y){ \frac {dy}{dt}}+y=0,\qquad \qquad (1)$

där ƒ ( y ) är en styckvis konstant funktion som är positiv, förutom liten y as

$f(y)={\begin{cases}-F,&|y|\leq Y_{0};\\F,&|y|>Y_{0}.\end{cases}}$

$F={\text{konstant}}>0,\quad Y_{0}={\text{konstant}}>0.$

Ekv. (1) är ett specialfall av Lienards ekvation ; den beskriver autosvängningarna.

Lösning (1) vid separata tidsintervall när f(y) är konstant ges av

$y_{k}(t)=A_{1 ,k}\exp(s_{1,k}t)+A_{2,k}\exp(s_{2,k}t)\qquad \qquad (2)$

Här ${\displaystyle s_{k}=F/2\mp {\sqrt {(F/2)^{2}-1}}} ,$ vid $|y|<Y_{0}$ och $s_{k}=-F/2\mp {\sqrt {( F/2)^{2}-1}}$ annars. Uttryck (2) kan användas för reella och komplexa värden på $s_{k}$ .

Första halvperiodens lösning vid $y(0)=\pm Y_{0}$ är

Avslappningssvängningar F = 4

$y(t)={\begin{cases}y_{1}(t),&0\leq t<T_{0};\\y_{ 2}(t),&T_{0}\leq t<T/2.\end{cases}}$

$y_{1}(t)=A_{1,k}\cdot \exp(s_{1,k}t)+A_{2,k}\cdot \exp(s_{2,k}t),$

$y_{2}(t)=A_{3,k}\cdot \exp(s_{3,k}t)+A_{4,k}\cdot \exp(s_{4,k}t) .$

Andra halvlekens lösning är

$y(t)={\begin{cases}-y_{1}(tT/2),&T/2\leq t<T/2+T_{0};\\-y_{2}(tT /2),&T/2+T_{0}\leq t<T.\end{cases}}$

Lösningen innehåller fyra integrationskonstanter $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ , perioden $T$ och gränsen $T_{0}$ mellan $y_{1}(t)$ och $y_{2 }(t)$ måste hittas. Ett gränsvillkor härleds från kontinuiteten av $y(t)$ ) och $dy/dt$ .

Lösning av (1) i stationärt läge erhålls således genom att lösa ett system av algebraiska ekvationer som

$y_{1}(0)=-Y_{0}$ ; $y_{1}(T_{0})=Y_{0}$ ; $y_{2}(T_{0})=Y_{0}$ ; $y_{2}(T/2)=Y_{0}$ ; $\left.{\begin{matrix}dy_{1}/dt\end{matrix}}\right|_{T_{0}}=\left.{\begin{matrix}dy_{2}/ dt\end{matris}}\right|_{T_{0}}$ ; $\left.{\begin{matrix}dy_{1}/dt\end{matrix}}\right|_{0}=-\left.{\begin{matrix}dy_{ 2}/dt\end{matris}}\right|_{T/2}\;\;\;(3)$ .

Integrationskonstanterna erhålls av Levenberg–Marquardt-algoritmen . Med $f(y)=\mu (-1+y^{2})$ , $\mu = const>0$ , ekv. (1) heter Van der Pol oscillator . Dess lösning kan inte uttryckas av elementära funktioner i sluten form.