Betyder absolut fel

Ej att förväxla med Genomsnittlig absolut avvikelse eller Genomsnittlig absolut skillnad .

I statistik är genomsnittligt absolut fel ( MAE ) ett mått på fel mellan parade observationer som uttrycker samma fenomen. Exempel på Y mot X inkluderar jämförelser av förutspådd kontra observerad, efterföljande tid mot initial tid, och en mätteknik kontra en alternativ mätteknik. MAE beräknas som summan av absoluta fel dividerat med urvalsstorleken :

$$\mathrm {MAE} ={\frac {\sum _{i=1}^{n}\left|y_{i}-x_{i}\right|}{n}}={\frac { \sum _{i=1}^{n}\left|e_{i}\right|}{n}}.$$

Det är alltså ett aritmetiskt medelvärde av de absoluta felen $|e_{i}|=|y_{i}-x_{i}|$ , där $y_{i}$ är förutsägelsen och $x_{i}$ den sanna värde. Observera att alternativa formuleringar kan inkludera relativa frekvenser som viktfaktorer. Det genomsnittliga absoluta felet använder samma skala som data som mäts. Detta är känt som ett skalberoende noggrannhetsmått och kan därför inte användas för att göra jämförelser mellan serier med olika skalor. Det genomsnittliga absoluta felet är ett vanligt mått på prognosfel i tidsserieanalys, som ibland används i förväxling med den mer standardiserade definitionen av genomsnittlig absolut avvikelse . Samma förvirring råder mer generellt.

Oenighet om kvantitet och oenighet om tilldelning

2 datapunkter för vilka kvantitetsskillnad är 0 och oenighet om allokering är 2 för både MAE och RMSE

Det är möjligt att uttrycka MAE som summan av två komponenter: Oenighet om kvantitet och Oenighet om allokering. Kvantitetsskillnad är det absoluta värdet av medelfelet som ges av:

$$\mathrm {ME} ={\frac {\sum _{i=1}^{n}y_{i}-x_{i}}{n}}.$$

Oenighet om allokering är MAE minus Oenighet om kvantitet.

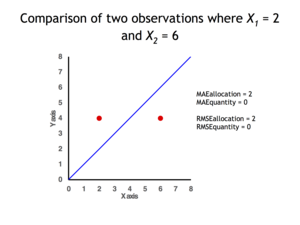
Det är också möjligt att identifiera olika typer av skillnader genom att titta på en $(x,y)$ plot. Kvantitetsskillnad föreligger när medelvärdet av X-värdena inte är lika med medelvärdet av Y-värdena. Tilldelningsskillnad finns om och endast om punkter finns på båda sidor om identitetslinjen.

Relaterade åtgärder

Det genomsnittliga absoluta felet är ett av flera sätt att jämföra prognoser med deras slutliga utfall. Väletablerade alternativ är det genomsnittliga absoluta skalade felet (MASE) och det genomsnittliga kvadratiska felet . Dessa sammanfattar alla prestanda på sätt som bortser från riktningen för över- eller underförutsägelser; ett mått som lägger tonvikt på detta är medelvärdet för teckenskillnaden .

När en prediktionsmodell ska anpassas med ett valt prestandamått, i den meningen att minsta kvadratmetoden är relaterad till medelkvadratfelet , är ekvivalenten för genomsnittligt absolut fel minsta absoluta avvikelser .

MAE är inte identisk med root-mean square error (RMSE), även om vissa forskare rapporterar och tolkar det så. MAE är begreppsmässigt enklare och också lättare att tolka än RMSE: det är helt enkelt det genomsnittliga absoluta vertikala eller horisontella avståndet mellan varje punkt i ett spridningsdiagram och Y=X-linjen. Med andra ord är MAE den genomsnittliga absoluta skillnaden mellan X och Y. Dessutom bidrar varje fel till MAE i proportion till felets absoluta värde. Detta till skillnad från RMSE som innebär att kvadrera skillnaderna, så att några få stora skillnader ökar RMSE i högre grad än MAE. Se exemplet ovan för en illustration av dessa skillnader.

Optimalitetsegenskap

  Det genomsnittliga absoluta felet för en reell variabel c med avseende på den slumpmässiga variabeln X är

$$E(\left|Xc\right|)$$

Förutsatt att sannolikhetsfördelningen av X är sådan att ovanstående förväntan existerar, då är m en median av X om och endast om m är en minimering av det genomsnittliga absoluta felet med avseende på X . I synnerhet m en urvalsmedian om och endast om m minimerar det aritmetiska medelvärdet av de absoluta avvikelserna.

Mer generellt definieras en median som ett minimum av

$$E(|Xc|-|X|),$$

som diskuterats vid Multivariat median (och specifikt vid Spatial median ).

Denna optimeringsbaserade definition av medianen är användbar vid statistisk dataanalys, till exempel vid k -medianklustring .

Bevis på optimalitet

Påstående: Klassificeraren som minimerar $\mathbb {E} |y-{\hat {y}}|$ är ${\hat {f}}(x)={ \text{Median}}(y|X=x)$ .

Bevis:

Förlustfunktionerna för klassificering är

$${\begin{aligned}L&=\mathbb {E} [|ya||X=x]\\&=\int _{-\infty }^{\infty }|ya |f_{Y|X}(y)\,dy\\&=\int _{-\infty }^{a}(ay)f_{Y|X}(y)\,dy+\int _{a} ^{\infty }(ya)f_{Y|X}(y)\,dy\\\end{aligned}}$$

Differentiera med avseende på en ger

$${\frac {\partial }{\partial a}}L=\int _{-\infty }^{a}f_{Y|X}(y)\,dy+\ int _{a}^{\infty }-f_{Y|X}(y)\,dy=0$$

Detta betyder

$$\int _{-\infty }^{a}f(y)\,dy=\int _{a}^ {\infty }f(y)\,dy$$

Därav

$$F_{Y|X}(a)=0,5$$

Se även

• Minsta absoluta avvikelser
• Genomsnittligt absolut procentuellt fel
• Medelprocentfel
• Symmetriskt medelvärde för absolut procentuellt fel