Inom vätskedynamik är Bermanflöde ett stadigt flöde skapat inuti en rektangulär kanal med två lika porösa väggar . Konceptet är uppkallat efter en vetenskapsman Abraham S. Berman som formulerade problemet 1953.
Flödesbeskrivning
Tänk på en rektangulär kanal med bredd mycket längre än höjden. Låt avståndet mellan den övre och nedre väggen vara  och välj koordinaterna så att
och välj koordinaterna så att  ligger mitt emellan de två väggarna, med
ligger mitt emellan de två väggarna, med  pekar vinkelrätt mot planen. Låt båda väggarna vara porösa med samma hastighet
pekar vinkelrätt mot planen. Låt båda väggarna vara porösa med samma hastighet  . Då blir kontinuitetsekvationen och Navier–Stokes ekvationer för inkompressibel vätska
. Då blir kontinuitetsekvationen och Navier–Stokes ekvationer för inkompressibel vätska

med randvillkor

Gränsförhållandena i centrum beror på symmetri. Eftersom lösningen är symmetrisk ovanför planet  räcker det att endast beskriva hälften av flödet, säg för
räcker det att endast beskriva hälften av flödet, säg för  . Om vi letar efter
. Om vi letar efter  en lösning, som är oberoende av
en lösning, som är oberoende av  dikterar kontinuitetsekvationen att den horisontella hastigheten
dikterar kontinuitetsekvationen att den horisontella hastigheten  som mest kan vara en linjär funktion av
som mest kan vara en linjär funktion av  . Därför introducerade Berman följande form,
. Därför introducerade Berman följande form,
![{\displaystyle \eta ={\frac {y}{h}},\quad \psi (x,\eta )=[h{\bar {u}}_{o}-xV]f(\eta ),\quad u=\left({\bar {u}}_{o}-{\frac {Vx}{h}}\right)f'(\eta ),\quad v=Vf(\eta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a303c6e6f6de690536d414b55db861fea86f75d)
där  är medelvärdet (genomsnittligt i tvärsnitt) av
är medelvärdet (genomsnittligt i tvärsnitt) av  vid
vid  , det vill säga
, det vill säga
![{\displaystyle {\bar {u}}_{0}={\frac {1}{2}}\int _{-1}^{1}u(0,\eta )d\eta ={\frac {{\bar {u}}_{0}}{2}}\int _{-1}^{1}f'(\eta )d\eta ={\frac {{\bar {u}}_{0}}{2}}[f(1)-f(-1)]={\bar {u}}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55fcd386ac883fa87d5ac3c6a41e33feeb1a2ae3)
Denna konstant kommer att elimineras ur problemet och kommer inte att påverka lösningen. Att ersätta detta i momentumekvationen leder till
![{\displaystyle {\begin{aligned}-{\frac {1}{\rho }}{\frac {\partial p}{\partial x}}&=\left({\bar {u}}_{o}-{\frac {Vx}{h}}\right)\left(-{\frac {V}{h}}[f'^{2}-ff'']-{\frac {\nu }{h^{2}}}f'''\right),\\-{\frac {1}{\rho }}{\frac {\partial p}{\partial \eta }}&=\nu {\frac {dv}{d\eta }}-{\frac {\nu }{h}}{\frac {d^{2}v}{d\eta ^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13ac2b7e0ce1664276fc57d29d755f8f3e9a0348)
Att differentiera den andra ekvationen med avseende på  ger
ger  detta kan ersättas med den första ekvation efter att ha tagit derivatan med avseende på
detta kan ersättas med den första ekvation efter att ha tagit derivatan med avseende på  vilket leder till
vilket leder till

där  är Reynolds-talet . Att integrera en gång får vi
är Reynolds-talet . Att integrera en gång får vi

med randvillkor

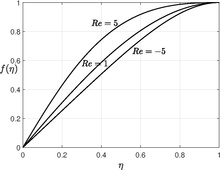
Denna ickelinjära ordinarie differentialekvation av tredje ordningen kräver tre gränsvillkor och det fjärde gränsvillkoret är att bestämma konstanten  . och denna ekvation har visat sig ha flera lösningar. Figuren visar den numeriska lösningen för lågt Reynolds tal, att lösa ekvationen för stort Reynolds tal är inte en trivial beräkning.
. och denna ekvation har visat sig ha flera lösningar. Figuren visar den numeriska lösningen för lågt Reynolds tal, att lösa ekvationen för stort Reynolds tal är inte en trivial beräkning.
Begränsande lösningar
I gränsen  kan lösningen skrivas som
kan lösningen skrivas som

I gränsen  ges ledande ordningens lösning av
ges ledande ordningens lösning av

Ovanstående lösning uppfyller alla nödvändiga randvillkor även om Reynolds tal är oändligt (se även Taylor–Culick-flöde )
Axisymmetriskt fall
Motsvarande problem i porösa rörflöden togs upp av SW Yuan och A. Finkelstein 1955.
Se även











![{\displaystyle \eta ={\frac {y}{h}},\quad \psi (x,\eta )=[h{\bar {u}}_{o}-xV]f(\eta ),\quad u=\left({\bar {u}}_{o}-{\frac {Vx}{h}}\right)f'(\eta ),\quad v=Vf(\eta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a303c6e6f6de690536d414b55db861fea86f75d)


![{\displaystyle {\bar {u}}_{0}={\frac {1}{2}}\int _{-1}^{1}u(0,\eta )d\eta ={\frac {{\bar {u}}_{0}}{2}}\int _{-1}^{1}f'(\eta )d\eta ={\frac {{\bar {u}}_{0}}{2}}[f(1)-f(-1)]={\bar {u}}_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55fcd386ac883fa87d5ac3c6a41e33feeb1a2ae3)
![{\displaystyle {\begin{aligned}-{\frac {1}{\rho }}{\frac {\partial p}{\partial x}}&=\left({\bar {u}}_{o}-{\frac {Vx}{h}}\right)\left(-{\frac {V}{h}}[f'^{2}-ff'']-{\frac {\nu }{h^{2}}}f'''\right),\\-{\frac {1}{\rho }}{\frac {\partial p}{\partial \eta }}&=\nu {\frac {dv}{d\eta }}-{\frac {\nu }{h}}{\frac {d^{2}v}{d\eta ^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13ac2b7e0ce1664276fc57d29d755f8f3e9a0348)